Python之算法模型-5.1
一、这里学习的算法模型包含监督学习和非监督学习两个方式的算法。
其中监督学习的主要算法分为(分类算法,回归算法),无监督学习(聚类算法),这里的几种算法,主要是学习他们用来做预测的效果和具体的使用方式。
二、分类算法
1)K-近邻算法
a、公式
2个样本,3个特征
a(a1,a2,a3),b(b1,b2,b3)
欧式距离:
____________________________________
p = √(a1 -b1)^2 + (a2-b2)^2 + (a3 - b3)^2
b、说明:K-近邻算法,简而言之,就是谁理我近,我就是这个分类。2个样本之间的距离通过公式得出p,p越小越接近改正确值的分类。
c、优缺点
优点:
简单、易于理解、易于实现、无需估计参数、无需训练
缺点:
懒惰算法,对测试样本分类时的计算量大,内存开销大
必须指定K值,K值选择不当则分类精度不能保证
问题:
k值比较小:容易受异常点影响
k值比较大:容易受K值影响(类别)影响
性能问题:每一个数据都要循环计算
说明:为了避免使用最小的值来确认分类,所以需要确定K值(即相邻个数),通过概率的方式进行选择分类
d、算法实现
# k-近邻算法 def k_near(): """ 2个样本,3个特征 a(a1,a2,a3),b(b1,b2,b3) 欧式距离: ____________________________________ p = √(a1 -b1)^2 + (a2-b2)^2 + (a3 - b3)^2 """ # 1、原始数据 # 读取数据 train_data = pandas.read_csv("k_near/train.csv") # print(train_data.head(10)) # 2、数据处理 # 数据筛选 train_data = train_data.query("x > 1.0 & x < 1.25 & y > 2.5 & y < 2.75") # 转换时间 time_value = pandas.to_datetime(train_data["time"], unit="s") # 转换成字典 time_value = pandas.DatetimeIndex(time_value) # print(time_value) # 构造特征 data = train_data.copy() data["day"] = time_value.day data["hour"] = time_value.hour data["weekday"] = time_value.weekday # print(train_data.head(10)) # 删除影响特征的数据,axis为1纵向删除 data = data.drop(["time"], axis=1) # 删除小于目标值的数据 place_count = data.groupby("place_id").count() # print(place_count) # 过滤数量大于5的地点ID,并且加入列中 tf = place_count[place_count.x > 5].reset_index() # print(tf) data = data[data["place_id"].isin(tf.place_id)] # 取特征值和目标值 y = data["place_id"] x = data.drop(["place_id", "row_id"], axis=1) # 数据分割 x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.25) # 3、特征工程 # 特征工程(标准化) std = StandardScaler() x_train = std.fit_transform(x_train) x_test = std.transform(x_test) # 4、算法 # 算法计算 """ 优点: 简单、易于理解、易于实现、无需估计参数、无需训练 缺点: 懒惰算法,对测试样本分类时的计算量大,内存开销大 必须指定K值,K值选择不当则分类精度不能保证 问题: k值比较小:容易受异常点影响 k值比较大:容易受K值影响(类别)影响 性能问题:每一个数据都要循环计算 """ # k值就是n_neighbors,也就是通过多少个邻近数据确认分类 knn = KNeighborsClassifier(n_neighbors=5) knn.fit(x_train, y_train) y_predict = knn.predict(x_test) print("预测值:", y_predict) # 5、评估 # 评估 score = knn.score(x_test, y_test) print("准确率:", score)
结果:

如果觉得上面的例子太复杂,那我们简化一下:
# K-近邻算法 def k_near_test(): # 1、原始数据 li = load_iris() # print(li.data) # print(li.DESCR) # 2、处理数据 data = li.data target = li.target x_train, x_test, y_train, y_test = train_test_split(data, target, test_size=0.25) # 3、特征工程 std = StandardScaler() x_train = std.fit_transform(x_train, y_train) x_test = std.transform(x_test) # 4、算法 knn = KNeighborsClassifier(n_neighbors=2) knn.fit(x_train, y_train) # 预估 y_predict = knn.predict(x_test) print("预估值:", y_predict) # 5、评估 source = knn.score(x_test, y_test) print("准确率:", source) """ 交叉验证与网格搜索: 交叉验证: 1、将一个训练集分成对等的n份(cv值) 2、将第一个作为验证集,其他作为训练集,得出准确率 3、将第二个作为验证集,其他作为训练集,知道第n个为验证集,得出准确率 4、把得出的n个准确率,求平均值,得出模型平均准确率 网格搜索: 1、用于参数的调整(比如,k近邻算法中的n_neighbors值) 2、通过不同参数传入进行验证(超参数),得出最优的参数值(最优n_neighbors值) """ # 4、算法 knn_gc = KNeighborsClassifier() # 构造值进行搜索 param= {"n_neighbors": [2, 3, 5]} # 网格搜索 gc = GridSearchCV(knn_gc, param_grid=param,cv=4) gc.fit(x_train, y_train) # 5、评估 print("测试集的准确率:", gc.score(x_test, y_test)) print("交叉验证当中最好的结果:", gc.best_score_) print("选择最好的模型:", gc.best_estimator_) print("每个超参数每次交叉验证结果:", gc.cv_results_)
结果:
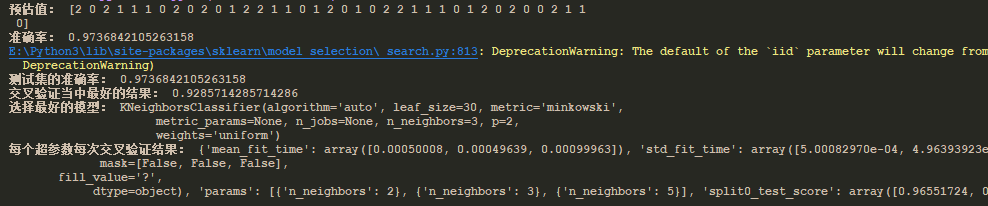
其实从上面的准确率来说,这个算法的可行度很低,下面这个是用sklearn 提供的数据集来做的测试,数据精准度比较高。
a、公式
贝叶斯公式: P(W|C)P(C) P(C|W) = —————————— P(W) 说明:P为概率,|在C的前提下W的概率, C分类, W多个条件(特征值)
说明:P(W|C)为:C的条件下:P(W1) * P(W2) * ...
拉普拉斯平滑:
拉普拉斯平滑:
避免出现次数为0的时候,计算结果直接为0
Ni + a
P(F1|C) = ———————
N + am
说明:a指系数一般为1, m为W(多个条件)的个数,NI为每个条件的个数,N为W(多个条件)的总个数
说明:为什么要存在拉普拉斯平滑,因为在P(W|C)中,在C分类的条件下,W为多个特征,但是如果W中存在一个为0的情况,那个整个结果就为0,这样不合理。概率统计,为了是统计在分类条件下,特征的成立数
平滑前:P(W|C) = P(W1=Ni/N)
平滑后:P(W|C) = P(W1=(Ni + a)/(N + am)),其中m为特征数
b、优缺点
优点: 源于古典数学理论,有稳定的分类效率 对缺失数据不太敏感,算法比较简单,常用语文本 分类精确度高,速度快 缺点: 使用样本属性独立性假设,与样本属性关联密切。如果训练集准确率不高,会影响结果
c、应用(由于数据的独立性影响,朴素贝叶斯算法一般用于文本等处理)
文本分类
from sklearn.datasets import fetch_20newsgroups from sklearn.feature_extraction.text import TfidfVectorizer from sklearn.metrics import classification_report from sklearn.model_selection import train_test_split from sklearn.naive_bayes import MultinomialNB # 朴素贝叶斯 def bayes(): """ 贝叶斯公式: P(W|C)P(C) P(C|W) = —————————— P(W) 说明:P为概率,|在C的前提下W的概率, C分类, W多个条件(特征值) 文档: P(C):每个文档类别的概率(某文档类别数/文档类别总数) P(W|C):给定类别特征(被预测文档中出现的词)的概率 拉普拉斯平滑: 避免出现次数为0的时候,计算结果直接为0 Ni + a P(F1|C) = ——————— N + am 说明:a指系数一般为1, m为W(多个条件)的个数,NI为每个条件的个数,N为W(多个条件)的总个数 优点: 源于古典数学理论,有稳定的分类效率 对缺失数据不太敏感,算法比较简单,常用语文本 分类精确度高,速度快 缺点: 使用样本属性独立性假设,与样本属性关联密切。如果训练集准确率不高,会影响结果 """ # 1、原始数据 news = fetch_20newsgroups() # 2、处理数据 x_train, x_test, y_train, y_test = train_test_split(news.data, news.target, test_size=0.25) print(x_train) # 3、特征工程 # 抽取特征数据 tf = TfidfVectorizer() # 训练集中词的重要性统计 x_train = tf.fit_transform(x_train) # print(tf.get_feature_names()) # 根据训练集转换测试集 x_test = tf.transform(x_test) # 4、算法 mlt = MultinomialNB() mlt.fit(x_train, y_train) y_predict = mlt.predict(x_test) print("预测值:", y_predict) # 5、评估 source = mlt.score(x_test, y_test) print("准确率:", source) # 精准率和召回率 """ 二分类的算法评价指标(准确率、精准率、召回率、混淆矩阵、AUC) 数据: 预测值 0 预测值 1 真实值 0 TN FP 真实值 1 FN TP 精准率(precision): TP precision = —————— TP + FP 召回率(recall): TP recall = ——————— TP + FN 模型的稳定性: 2TP 2precision * recall F1 = ————————————— = ——————————————————— 2TP + FN + FP precision + recall """ print("精准率和召回率:\n", classification_report(y_test, y_predict, target_names=news.target_names))
e、结果
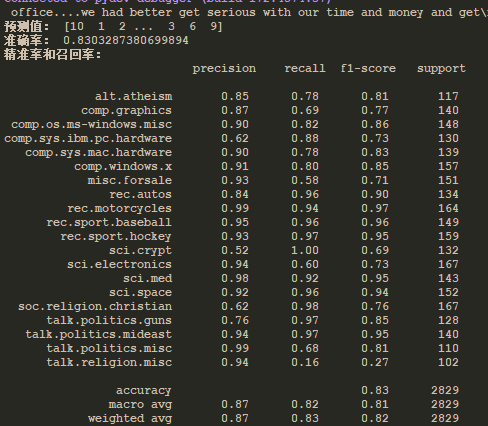
3)决策树和随机森林
a、公式
信息熵:
n
H(X) = - ∑ p(x)logp(x)
i=1
说明:log 低数为2,单位比特,H(X)为熵,x为特征具体值,p(x)为该值在x特征值中的概率
信息增益:
g(D, A) = H(D) - H(D|A)
说明:随机森林是在决策树的基础上,种植多颗树的方式,只是每一颗树的深度没有决策树那么深。
特征复杂度决定了决策树的深度,不是树的深度越深,就越好的,有可能存在计算不出结果。
信息熵:是确定树深度的最大值。
信息增益:得知特征X的信息而使得类Y的信息的不确定性的减少程度。
b、优缺点
优点:
简化理解和解释,树木可视化
需要很少的数据准备,其他技术通常需要数据归一化
缺点:
树太过于复杂,过拟合
改进:
减枝cart算法(决策树API中已经实现)
随机森林:
在当前所有算法中具有极好的准确率
能够有效的运行在大数据集上
能够处理具有高维特征的输入样本中,而且不需要降维
能够评估各个特征在分类问题上的重要性
c、代码实现
# 决策树和随机森林 def decision_tree(): """ 决策树: 信息熵: n H(X) = - ∑ p(x)logp(x) i=1 说明:log 低数为2,单位比特,H(X)为熵,x为特征具体值,p(x)为该值在x特征值中的概率 信息增益: g(D, A) = H(D) - H(D|A) 优点: 简化理解和解释,树木可视化 需要很少的数据准备,其他技术通常需要数据归一化 缺点: 树太过于复杂,过拟合 改进: 减枝cart算法(决策树API中已经实现) 随机森林: 在当前所有算法中具有极好的准确率 能够有效的运行在大数据集上 能够处理具有高维特征的输入样本中,而且不需要降维 能够评估各个特征在分类问题上的重要性 """ # 1、原始数据 taitan = pandas.read_csv("decision_tree/titanic.csv") # 2、数据处理 x = taitan[["pclass", "age", "sex"]] y = taitan["survived"] # 缺失值处理 x["age"].fillna(x["age"].mean(), inplace=True) x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.25) # 3、特征工程 # 采用DictVectorizer目的是,数据更多是文本类型的,借助dict的方式来处理成0/1的方式 dict = DictVectorizer(sparse=True) x_train = dict.fit_transform(x_train.to_dict(orient="records")) # print(x_train) x_test = dict.transform(x_test.to_dict(orient="records")) # print(dict.get_feature_names()) # 4、算法 tree = DecisionTreeClassifier() tree.fit(x_train, y_train) # 5、评估 score = tree.score(x_test, y_test) print("准确率:", score) # 导出决策树图形 export_graphviz(tree, out_file="decision_tree/tree.dot", feature_names=['年龄', 'pclass=1st', 'pclass=2nd', 'pclass=3rd', '女', '男']) # 随机森林 # 4、算法 rf = RandomForestClassifier() # 超参数调优 # 网络搜索与交叉验证 params = { "n_estimators": [120, 200, 300, 500, 800, 1200], "max_depth": [5, 8, 15, 25, 30] } gc = GridSearchCV(rf, param_grid=params, cv=4) gc.fit(x_train, y_train) # 5、评估 score = gc.score(x_test, y_test) print("准确率:", score) print("最佳参数模型:", gc.best_params_)
n_estimators:随机森林数量, max_depth:最大深度
d、结果

三、回归算法
1)矩阵计算
矩阵:
必须是二维
乘法公式:
(m行, l列)* (l行, n列) = (m行, n列)
例如:
[[1,2,3,4]] * [[5],[6],[7],[8]] = 5 * 1 + 6 * 2 + 7 * 3 + 8 * 4
2)线性回归
a、正规线性公式
属性的线性组合: f(x) = w1x1 + w2x2 + w3x3 + ... + wnxn + b w:权重, b偏置项, x:特征数据 b:单个特征是更加通用 线性回归: 通过一个或者多个自变量与因变量之间进行建模的回归分析 其中可以为一个或者多个自变量之间的线性组合(线性回归的一种) 一元线性回归: 涉及的变量只有一个 多元线性回归: 涉及变量为两个或者两个以上 通用公式: h(w) = w0 + w1x1 + w2x2 + ... + wnxn w,x为矩阵w0为b
b、损失函数(最小二乘法)
损失函数(最小二乘法)(误差的平方和):
j(θ) = (hw(x1) - y1)^2 + (hw(x2) - y2)^2 + ... + (hw(xn) - yn)^2
n
= ∑(hw(xi) - yi)^2
i=1
yi:训练样本的真实值, hw(xi):第i个训练样本的特征、组合预测值
说明:当损失值在最小的时候,说明,函数的拟合状态最好,这种方式,也就更加接近具体的预测轨迹
c、权重值
正规方程:
W = (XtX)^(-1)XtY
X:特征值矩阵, Y:目标值矩阵 Xt:转置特征值(行列替换)
特征比较复杂时,不一定能得出结果
梯度下降:
例子(单变量):
δcost(w0 + w1x1) ||
w1 = -w1 - α———————————————— ||
δw1 || (下降)
δcost(w0 + w1x1) ||
w0 = -w0 - α———————————————— ||
δw1 \/
α:学习速率,需要手动指定
δcost(w0 + w1x1)
———————————————— 表示方向
δw1
说明:在求最小损失值的时候,需要不断的求解W(权重值),权重值的求解方式一般为上面两种。求出的值,然后在计算损失值,然后在反过来推导,权重值。如此得出结果,速率越慢当然拟合程度越高,但都是拟合越高越好。
欠拟合:
原因:
学习到的特征太少
解决办法:
增加数据的特征数量
过拟合(训练集和测试集表现不好):
原因:
原始特征数量过多,存在一些嘈杂的特征,模型过于复杂是因为模型尝试去兼顾各个测试数据点
解决办法:
进行特征选择,消除一些关联性不大的特征(不好做)
交叉验证(让所有数据进行训练)
正则化
表现形式:

最理想的状态不是第三种,而是第二种。
d、对比:
对比:
梯度下降:
1、需要选择学习率α
2、需要多次迭代
3、当特征数量n很大时,也比较适用
4、适用于各种类型的模型
正规方程:
1、不需要选择学习率α
2、一次运算得出
3、需要计算(XtX)^(-1), 如果特征数量n很大时,时间复杂度很高,通常n<100000,可以接受
4、只能用于线性模型,不适合逻辑回归模型等其他模型
3)岭回归
a、存在的意义
岭回归:
1、因为线性回归(LinearRegression)容易出现过拟合的情况,所有需要正则化
2、正则化的目的,就是将高幂(x^n,n很大),的权重降到接近于0
3、岭回归为带有正则化的线性回归
4、回归得到的系数更加符合实际,更加可靠,更存在病态数据偏多的研究中存在较大价值
说明:求解模型f(x) = w0 + w1*x1 + w2*x2^2 + ... + wn*xn^n的时候,减少x^n的权重,这样就减少了过拟合(上图第三种)的方式
b、优势
1、具有l2正则化的线性最小二乘法
2、alpha(λ):正则化力度
3、coef_:回归系数
4)代码实现
from sklearn.datasets import load_boston from sklearn.linear_model import LinearRegression, SGDRegressor, Ridge from sklearn.model_selection import train_test_split from sklearn.preprocessing import StandardScaler from sklearn.metrics import mean_squared_error def regression(): """ 属性的线性组合: f(x) = w1x1 + w2x2 + w3x3 + ... + wnxn + b w:权重, b偏置项, x:特征数据 b:单个特征是更加通用 线性回归: 通过一个或者多个自变量与因变量之间进行建模的回归分析 其中可以为一个或者多个自变量之间的线性组合(线性回归的一种) 一元线性回归: 涉及的变量只有一个 多元线性回归: 涉及变量为两个或者两个以上 通用公式: h(w) = w0 + w1x1 + w2x2 + ... + wnxn w,x为矩阵w0为b 矩阵: 必须是二维 乘法公式: (m行, l列)* (l行, n列) = (m行, n列) 例如: [[1,2,3,4]] * [[5],[6],[7],[8]] = 5 * 1 + 6 * 2 + 7 * 3 + 8 * 4 损失函数(最小二乘法)(误差的平方和): j(θ) = (hw(x1) - y1)^2 + (hw(x2) - y2)^2 + ... + (hw(xn) - yn)^2 n = ∑(hw(xi) - yi)^2 i=1 yi:训练样本的真实值, hw(xi):第i个训练样本的特征、组合预测值 权重: 正规方程: W = (XtX)^(-1)XtY X:特征值矩阵, Y:目标值矩阵 Xt:转置特征值(行列替换) 特征比较复杂时,不一定能得出结果 梯度下降: 例子(单变量): δcost(w0 + w1x1) || w1 = -w1 - α———————————————— || δw1 || (下降) δcost(w0 + w1x1) || w0 = -w0 - α———————————————— || δw1 \/ α:学习速率,需要手动指定 δcost(w0 + w1x1) ———————————————— 表示方向 δw1 回归性能评估: 1 m _ MSE = ——— ∑(yi - y)^2 m i=1 _ yi:预测值 y:真实值 一定要标准化之前的值 对比: 梯度下降: 1、需要选择学习率α 2、需要多次迭代 3、当特征数量n很大时,也比较适用 4、适用于各种类型的模型 正规方程: 1、不需要选择学习率α 2、一次运算得出 3、需要计算(XtX)^(-1), 如果特征数量n很大时,时间复杂度很高,通常n<100000,可以接受 4、只能用于线性模型,不适合逻辑回归模型等其他模型 岭回归: 1、因为线性回归(LinearRegression)容易出现过拟合的情况,所有需要正则化 2、正则化的目的,就是将高幂(x^n,n很大),的权重降到接近于0 3、岭回归为带有正则化的线性回归 4、回归得到的系数更加符合实际,更加可靠,更存在病态数据偏多的研究中存在较大价值 Ridge: 1、具有l2正则化的线性最小二乘法 2、alpha(λ):正则化力度 3、coef_:回归系数 """ # 1、获取数据 lb = load_boston() # 2、处理数据 # 分隔数据 x_train, x_test, y_train, y_test = train_test_split(lb.data, lb.target, test_size=0.25) # 3、特征工程 # 数据标准化(目的,特征值差异过大,按比例缩小) # 目标值也要进行标准化(目的,特征值标准化后,特征值值过大在回归算法中,得出的权重值差异过大) # 两次标准化实例的目的,就是不同数据之间的实例化不一样 std_x = StandardScaler() x_train = std_x.fit_transform(x_train) x_test = std_x.transform(x_test) std_y = StandardScaler() # 目标值也要转成2维数组(-1,不知道样本数) y_train = std_y.fit_transform(y_train.reshape(-1, 1)) y_test = std_y.transform(y_test.reshape(-1, 1)) # print(x_train, y_train) # 4、线性回归正规算法 """ 1、通过结果可以看出真实值和预测值的差距还是很大的。 2、这是直接通过线性回归的正确公式来算出权重值的结果。 3、为了更好的减少误差,所以采用梯度下降的方式,来重新计算权重值 """ lr = LinearRegression() lr.fit(x_train, y_train) y_predict_lr = lr.predict(x_test) # 注意这里的预测值是标准化过后的数据,需要转回来 # print("预测值:", std_y.inverse_transform(y_predict_lr).reshape(1, -1)) # print("真实值:", std_y.inverse_transform(y_test).reshape(1, -1)) print("权重值:", lr.coef_) # 5、回归评估 print("正规方程均方误差:", mean_squared_error(std_y.inverse_transform(y_test).reshape(1, -1), std_y.inverse_transform(y_predict_lr).reshape(1, -1))) # 4、线性回归梯度下降算法 sgd = SGDRegressor() sgd.fit(x_train, y_train) y_predict_sgd = sgd.predict(x_test) # 注意这里的预测值是标准化过后的数据,需要转回来 # print("预测值:", std_y.inverse_transform(y_predict_sgd).reshape(1, -1)) # print("真实值:", std_y.inverse_transform(y_test).reshape(1, -1)) print("权重值:", sgd.coef_) # 5、回归性能评估 print("梯度下降均方误差:", mean_squared_error(std_y.inverse_transform(y_test).reshape(1, -1), std_y.inverse_transform(y_predict_sgd).reshape(1, -1))) # 4、线性回归正则化算法(岭回归) # alpha为超参数,可以通过网格搜索和交叉验证,来确认alpha的值 # alpha范围(0~1, 1~10) rd = Ridge(alpha=1.0) rd.fit(x_train, y_train) y_predict_rd = rd.predict(x_test) # 注意这里的预测值是标准化过后的数据,需要转回来 # print("预测值:", std_y.inverse_transform(y_predict_rd).reshape(1, -1)) # print("真实值:", std_y.inverse_transform(y_test).reshape(1, -1)) print("权重值:", sgd.coef_) # 5、回归性能评估 print("正则化均方误差:", mean_squared_error(std_y.inverse_transform(y_test).reshape(1, -1), std_y.inverse_transform(y_predict_sgd).reshape(1, -1)))
5)结果
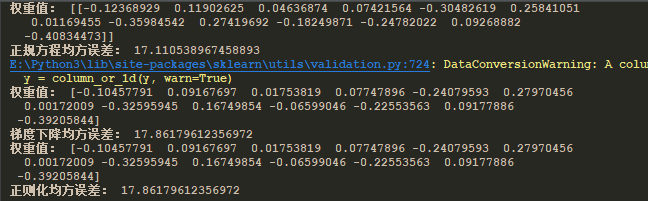
说明:从结果可以看出差异并不是很大,那是因为训练次数的原因,可以通过多次的训练来达到效果
四、逻辑回归
1)公式:
公式:
1
hθ = g(θ^Tx) = ————————————
1 + e^(-θ^Tx)
1
g(z) = ——————————
1 + e^(-z)
输入:[0,1]区间的概率,默认值0.5作为阈值
g(z):sigmoid函数,z为回归结果
说明:逻辑回归,是算一种二分类算法。比如:是否是猫、狗等。我们不能完全确认,他是否是猫,那就用概率的方式来确认分类。概率值越高说明是,反之否。通过大约阈值来确认分类,这种方式人图像识别中还是比较常用的方式。
2)损失函数:
损失函数:
与线性回归原理相同,但是由于是分类问题。损失函数不一样。
只能通过梯度下降求解。
对数似然损失函数:
{ -log(hθ(x)) if y = 1
cost(hθ(x), y) = {
{ -log(1 - hθ(x)) if y = 0
hθ(x)为x的概率值
说明:在均方误差中不存在多个最低点,但是对数似然损失函数,会存在多个低点的情况
完整的损失函数:
m
cost(hθ(x), y) = ∑-yilog(hθ(x)) - (1 - yi)log(1 - hθ(x))
i=1
cost损失值越小,那么预测的类别精准度更高
对数似然损失函数表现:(目前没有好的方式去解决确认最低点的问题)
改善方式:
1、多次随机初始化,多次比较最小值结果
2、求解过程中,调整学习率
上面两种方式只是改善,不是真正意义上的解决这个最低点的问题。虽然没有最低点,但是最终结果还是不错的。
损失函数,表现形式:
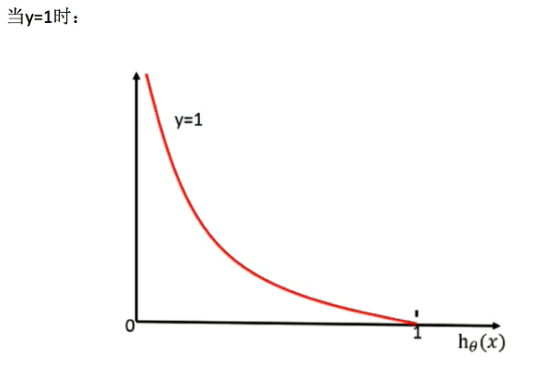
说明:如果真实值为y=1时,当hθ(x)的概率越接近1时,说明损失函数的值越小。图形公式 -log(P)

说明:如果真是值为y=0时,概率越小,损失值就越小
3)代码实现
import numpy import pandas from sklearn.linear_model import LogisticRegression from sklearn.preprocessing import StandardScaler from sklearn.model_selection import train_test_split from sklearn.metrics import mean_squared_error, classification_report # 逻辑回归 def logic_regression(): """ 公式: 1 hθ = g(θ^Tx) = ———————————— 1 + e^(-θ^Tx) 1 g(z) = —————————— 1 + e^(-z) 输入:[0,1]区间的概率,默认值0.5作为阈值 g(z):sigmoid函数,z为回归结果 损失函数: 与线性回归原理相同,但是由于是分类问题。损失函数不一样。 只能通过梯度下降求解。 对数似然损失函数: { -log(hθ(x)) if y = 1 cost(hθ(x), y) = { { -log(1 - hθ(x)) if y = 0 hθ(x)为x的概率值 说明:在均方误差中不存在多个最低点,但是对数似然损失函数,会存在多个低点的情况 完整的损失函数: m cost(hθ(x), y) = ∑-yilog(hθ(x)) - (1 - yi)log(1 - hθ(x)) i=1 cost损失值越小,那么预测的类别精准度更高 """ """ penalty:正则化方式默认值l2, C为回归系数默认值1.0 """ # 1、原始数据 # 地址:https://archive.ics.uci.edu/ml/machine-learning-databases/breast-cancer-wisconsin/ # 数据:https://archive.ics.uci.edu/ml/machine-learning-databases/breast-cancer-wisconsin/breast-cancer-wisconsin.data column_names = ["Sample code number", "Clump Thickness", "Uniformity of Cell Size", "Uniformity of Cell Shape", "Marginal Adhesion", "Single Epithelial Cell Size", "Bare Nuclei", "Bland Chromatin", "Normal Nucleoli", "Mitoses", "Class"] data = pandas.read_csv("classify_regression/breast-cancer-wisconsin.data", names=column_names) # print(data) # 2、数据处理 # 缺失值处理 data = data.replace(to_replace="?", value=numpy.NAN) # 删除缺失值数据 data = data.dropna() # 特征值,目标值 x = data[column_names[1:10]] y = data[column_names[10]] # 数据分割 x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.25) # 3、特征工程 std = StandardScaler() x_train = std.fit_transform(x_train, y_train) x_test = std.transform(x_test) # 4、算法工程 lr = LogisticRegression(penalty="l2", C=1.0) # 训练 lr.fit(x_train, y_train) print("权重值:", lr.coef_) # 5、评估 print("准确率:", lr.score(x_test, y_test)) y_predict = lr.predict(x_test) print("召回率:", classification_report(y_test, y_predict, labels=[2, 4], target_names=["良性", "恶性"])) print("均方误差:", mean_squared_error(y_test, y_predict))
4)结果:

五、上面说的都是监督学习的算法,下面介绍一种非监督学习的算法(k-mean)
1)步骤和优缺点
k值:
分类个数,一般是知道分类个数的,如果不知道,进行超参数设置
算法实现过程:
1)随机在数据中抽取K个样本,当做K个类别的中心点
2)计算其余的点到这K个点的距离,每一个样本有K个距离值,从中选出最近的一个距离点作为自己的标记
这样就形成了K个族群
3)计算着K个族群的平均值,把这K个平均值,与之前的K个中心点进行比较。
如果相同:结束聚类
如果不同:把K个平均值作为新的中心点,进行计算
优点:
采用迭代式算法,直观易懂并且非常实用
缺点:
容易收敛到局部最优解(多次聚类)
注意:聚类一般是在做分类之前
2)评估方式
轮廓系数:
bi - ai
sci = ———————————
max(bi, ai)
注:对于每个点i为已聚类数据中的样本,bi为i到其他族群的所有样本的距离
最小值,ai为i到本族群的距离平均值
最终算出所有的样本的轮廓系数平均值
sci范围:[-1, 1],越靠近1越好
3)代码实现方式
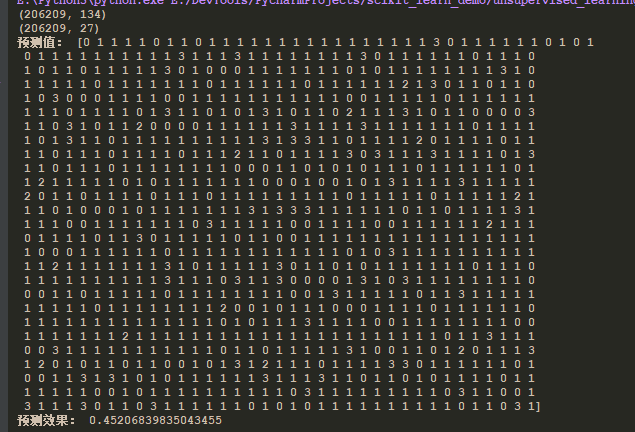
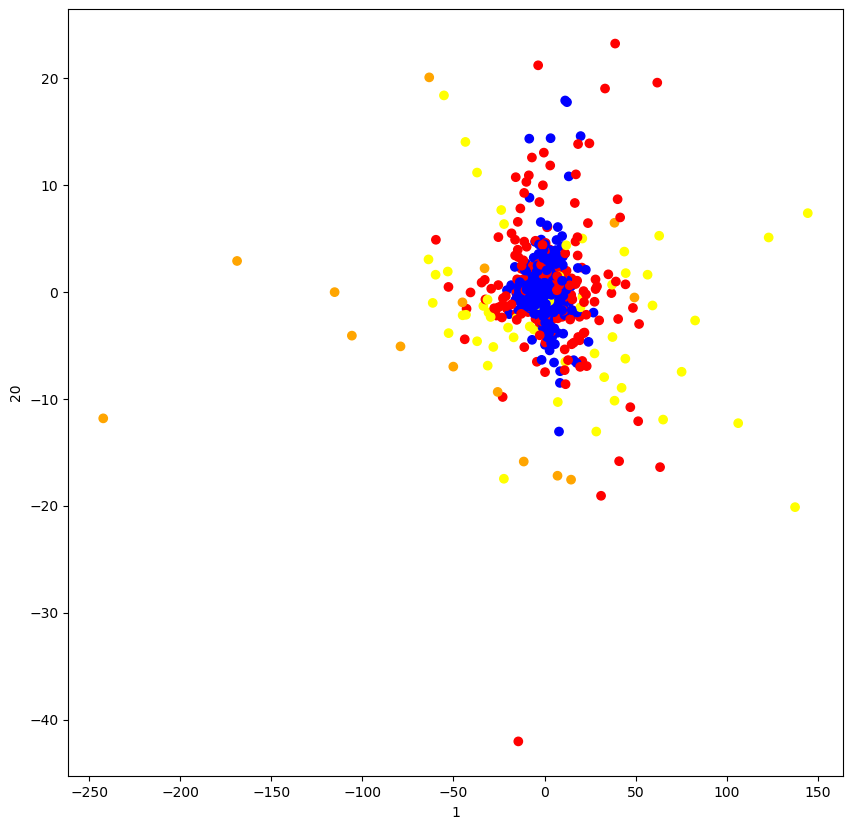
from matplotlib import pyplot import pandas from sklearn.cluster import KMeans from sklearn.decomposition import PCA from sklearn.metrics import silhouette_score # 聚类 def k_means(): """ k值: 分类个数,一般是知道分类个数的,如果不知道,进行超参数设置 算法实现过程: 1)随机在数据中抽取K个样本,当做K个类别的中心点 2)计算其余的点到这K个点的距离,每一个样本有K个距离值,从中选出最近的一个距离点作为自己的标记 这样就形成了K个族群 3)计算着K个族群的平均值,把这K个平均值,与之前的K个中心点进行比较。 如果相同:结束聚类 如果不同:把K个平均值作为新的中心点,进行计算 优点: 采用迭代式算法,直观易懂并且非常实用 缺点: 容易收敛到局部最优解(多次聚类) 注意:聚类一般是在做分类之前 """ # 1、原始数据 orders = pandas.read_csv("market/orders.csv") prior = pandas.read_csv("market/order_products__prior.csv") products = pandas.read_csv("market/products.csv") aisles = pandas.read_csv("market/aisles.csv") # 2、数据处理 # 合并数据 _msg = pandas.merge(orders, prior, on=["order_id", "order_id"]) _msg = pandas.merge(_msg, products, on=["product_id", "product_id"]) merge_data = pandas.merge(_msg, aisles, on=["aisle_id", "aisle_id"]) # 交叉表(特殊分组) # (用户ID, 类别) cross = pandas.crosstab(merge_data["user_id"], merge_data["aisle"]) print(cross.shape) # 3、特征工程 # 降维 pca = PCA(n_components=0.9) data = pca.fit_transform(cross) print(data.shape) # 4、算法 """ n_clusters:开始均值的中心数量 """ km = KMeans(n_clusters=4) #减少数据量 # data = data[1:1000] # 训练 km.fit(data) # 预测结果 predict = km.predict(data) print("预测值:", predict) # 5、评估 """ 轮廓系数: bi - ai sci = ——————————— max(bi, ai) 注:对于每个点i为已聚类数据中的样本,bi为i到其他族群的所有样本的距离 最小值,ai为i到本族群的距离平均值 最终算出所有的样本的轮廓系数平均值 sci范围:[-1, 1],越靠近1越好 """ print("预测效果:", silhouette_score(data, predict)) # 6、图形展示 pyplot.figure(figsize=(10, 10)) colors = ["red", "blue", "orange", "yellow"] color = [colors[i] for i in predict] pyplot.scatter(data[:, 1], data[:, 20], color=color) pyplot.xlabel("1") pyplot.ylabel("20") pyplot.show()
4)结果: