Python之特征工程-3

　　一、什么是特征工程？其实也是数据处理的一种方式，和前面的原始数据不一样的是，我们在原始数据的基础上面，通过提取有效特征，来预测目标值。而想要更好的去得出结果，包括前面使用的数据处理中数据特征提取，新增减少等手段都是特征功能的一种，这里为什么要单独提出来讲特征工程，而不是数据处理呢？

　　二、数据处理的方式有很多种方式，合并等。这里讲特征工程主要是讲转换器，为啥这样说呢，因为我们在使用数据的时候，比如：文本，那我们通过文本的方式去计算，这个方式不利于数学公式的发挥。那么问题来了，想要更好的使数据达到预测的效果，那数据的转换是很有必要的。

　　　　简单理解就是：将原本比如文本型的数据，进行中文分词过后，在将文本变换成数字，具体为一个二维的矩阵数据。

　　三、fit、transform、fit_transform

　　1）在转换其中存在三个函数分别为fit、transform、fit_transform，翻译为：学习，转换，学习和转换

　　2）fit中存在两个参数：X，y：即特征值，目标值。只传X，即为无监督学习。X，y都传，即监督学习（有意识的去靠近目标）

　　3）transform，按照学习后的方式，进行其他数据的学习。有点像吧学习好的方式，套用到其他数据集得出结果。

　　4）fit_transform，两种方式的结合。

　　四、转换器

　　1）字典（JSON）转换器

from sklearn.feature_extraction import DictVectorizer

# 字典特征提取
def dict_data():
    # sparse=False：one-hot, True:矩阵
    dict = DictVectorizer(sparse=True)
    data = dict.fit_transform([{"city": "四川", "temperature": 20}, {"city": "北京", "temperature": 30}])
    # 转换成矩阵
    print(data.toarray())
    # 特征名称
    print(dict.get_feature_names())
    # 逆向转换成字典
    print(dict.inverse_transform(X=data))

　　结果：

　　说明：可以看出，特征名称，是将不是数据的类型分开，通过0表示没有，1表示存在的方式形成矩阵数据

　　2）文本特征提取转换器

import jieba
from sklearn.feature_extraction.text import CountVectorizer

# 文本特征提取
def count_data():
    cv = CountVectorizer()
    # data = cv.fit_transform(["I love you", "I like you"])
    # data = cv.fit_transform(["人生 苦短 我 喜欢 Python", "人生 漫长 我 讨厌 Python"])
    # 中文文字分词
    data = cv.fit_transform([' '.join(jieba.cut("人生苦短，我喜欢Python")), ' '.join(jieba.cut("人生漫长，我讨厌Python"))])
    print(data.toarray())
    print(cv.get_feature_names())if __name__ == '__main__':
    count_data()

　　结果：

　　说明：文本特征提取的方式一般是通过中文分词的方式来处理的，因为英文默认是分开的所以好处理，但是中文需要分词器来处理。结果也是用0,1表示数据在样本中的数量。

　　3）tf_idf（term frequency and inverse document frequency）词的频率和逆文档频率。（逆文档频率公式：log(总文档数量/改词频率)）

import jieba
from sklearn.feature_extraction.text import TfidfVectorizer

# term frequency(词出现的频率) and inverse document frequency(log(总文档数量/改词频率))
def tf_idf_data():
    cv = TfidfVectorizer()
    # data = cv.fit_transform(["I love you", "I like you"])
    # data = cv.fit_transform(["人生 苦短 我 喜欢 Python", "人生 漫长 我 讨厌 Python"])
    data = cv.fit_transform([' '.join(jieba.cut("人生苦短，我喜欢Python")), ' '.join(jieba.cut("人生漫长，我讨厌Python"))])
    print(data.toarray())
    # 特征名称
    print(cv.get_feature_names())

　　结果：

　　说明：单文字不做计算，他是通过文章中出现的词的频率越少，确认他的权重越高。tf-idf具体计算过程可以参考：https://baike.baidu.com/item/tf-idf/8816134?fr=aladdin

　　4）归一化

　　a、公式：

          　　x - min
        x' = —————————
             max - min

        x" = x'(mx - mi) + mi
        (default mx = 1, mi = 0)
        mi, mx为区间，min, max为一中特征总的最小最大值。x为实际值，x"为最终结果

　　b、代码实现

from sklearn.preprocessing import MinMaxScaler

# 归一化
def normalize_data():
    """
    数据：
        30 10 20
        70 30 50
        110 50 35
    公式：
              x - min
        x' = —————————
             max - min

        x" = x'(mx - mi) + mi
        (default mx = 1, mi = 0)
        mi, mx为区间，min, max为一中特征总的最小最大值。x为实际值，x"为最终结果
    """
    # feature_range指数据区间默认（0, 1）
    mms = MinMaxScaler(feature_range=(2, 3))
    data = mms.fit_transform([[30, 10, 20], [70, 30, 50], [110, 50, 35]])
    print(data)

 　　c、结果：

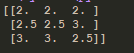
　　d、说明：归一化的目的是将数据，按照比例的方式缩小，以减少，由于某个特征值，特别大引起权重的变化。

　　e、缺点：容易受到单个特征值的影响，在公式中x'为计算结果，如果max是异常点很大，那么其他数据结果，值就会特别小。会让数据的权重值下降。所以一般不采用这种方式。

　　5）标准化

　　a、公式

　　　　 方差:
              (x1 - avg)^2 + (x2 - avg)^2 + ...
        var = —————————————————————————————————
                            n
        标准差：
             ___
        a = √var
             x - avg
        x' = ————————
                a
        avg为平均值,x'为最终结果

　　b、代码实现

from sklearn.preprocessing import StandardScaler

# 标准化
def standard_data():
    """
    公式：
        方差:
              (x1 - avg)^2 + (x2 - avg)^2 + ...
        var = —————————————————————————————————
                            n
        标准差：
             ___
        a = √var
             x - avg
        x' = ————————
                a
        avg为平均值,x'为最终结果
    """
    ss = StandardScaler()
    data = ss.fit_transform([[30, 10, 20], [70, 30, 50], [110, 50, 35]])
    print(data)

　　c、结果

　　d、说明：数据标准化会受到单个异常点的影响，但是影响不大。这种方式得出的结果，针对于数据来说比较平均，是比较常见的一种方式。标准化的目的也是为了减少实际数据中特征值的影响。当特征都区域统一权重状态。

　　6）降维(PCA，又称主成分分析)

　　a、方式：通过计算获取特征值结果，如果一个特征中的数据差异很小，就可以降维（即删除此特征）。保留有用的特征数据。

　　b、代码实现

import pandas
from sklearn.decomposition import PCA

# 降维
def dimensionality_reduction():
    # 读取数据
    orders = pandas.read_csv("market/orders.csv")
    prior = pandas.read_csv("market/order_products__prior.csv")
    products = pandas.read_csv("market/products.csv")
    aisles = pandas.read_csv("market/aisles.csv")
    # 合并数据
    _msg = pandas.merge(orders, prior, on=["order_id", "order_id"])
    _msg = pandas.merge(_msg, products, on=["product_id", "product_id"])
    merge_data = pandas.merge(_msg, aisles, on=["aisle_id", "aisle_id"])
    # 交叉表(特殊分组)
    # （用户ID， 类别）
    cross = pandas.crosstab(merge_data["user_id"], merge_data["aisle"])
    print(cross.shape)
    # 降维
    pca = PCA(n_components=0.9)
    data = pca.fit_transform(cross)
    # 查看数据量和结果
    print(data.shape)

　　说明：n_components为数据保留率一般（90%~95%）

　　c、结果：

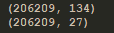
　　d、解释：这里的134为原始数据的特征数量，27为降维过后的特征数量，从计算上面来看，已经达到效果了。