bzoj 4766: 文艺计算姬 -- 快速乘

4766: 文艺计算姬

Time Limit: 1 Sec  Memory Limit: 128 MB

Description

"奋战三星期，造台计算机"。小W响应号召，花了三星期造了台文艺计算姬。文艺计算姬比普通计算机有更多的艺

术细胞。普通计算机能计算一个带标号完全图的生成树个数，而文艺计算姬能计算一个带标号完全二分图的生成树

个数。更具体地，给定一个一边点数为n，另一边点数为m，共有n*m条边的带标号完全二分图K_{n,m}，计算姬能快

速算出其生成树个数。小W不知道计算姬算的对不对，你能帮助他吗？

 

 

Input

仅一行三个整数n,m,p，表示给出的完全二分图K_{n,m}

1 <= n,m,p <= 10^18

 

 

Output

仅一行一个整数，表示完全二分图K_{n,m}的生成树个数，答案需要模p。

 

 

Sample Input

2 3 7

Sample Output

5

HINT

我们可以用矩阵树定理或prufer序列证明其生成树个数为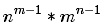

因为由于模数比较大，乘法会爆long long 所以需要用到快速乘

#include<cstdio>
typedef long long ll;
typedef long double ld;
ll n,m,p;
ll mul(ll x,ll y){return (x*y-(ll)(((ld)x*y+0.5)/(ld)p)*p+p)%p;}
ll ksm(ll a,ll b)
{
    ll ret=1;
    for(;b;b>>=1,a=mul(a,a))
        if(b&1) ret=mul(ret,a);
    return ret;
}
int main()
{
    scanf("%lld%lld%lld",&n,&m,&p);
    printf("%lld\n",mul(ksm(n,m-1),ksm(m,n-1)));
}