半平面交学习笔记

半平面交 - (S & I algorithm)

参考论文 算法合集之《半平面交的新算法及其实用价值》

问题简介:

给出多个如 \(ax + by + c \ge 0\) 的限制( 接下来都以 \(ax+by+c \ge 0\) 为例) , 求解 \((x,y)\) 的集合

可以转化为多个直线在平面上围成的凸包

step1

将所有直线按角度排序,角度相同的保留下需要的一个(如图)

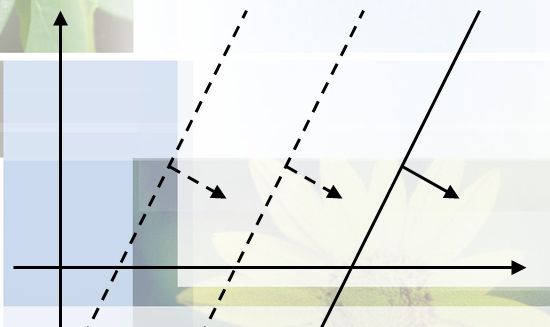
step2

用一个双端队列存储当前半平面交,每次通过判断队首与队尾第一个交点是否满足当前直线来更新

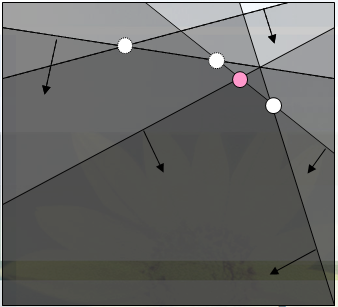
step3

先用队尾判定队首交点是否合法,再用队首判断队尾交点是否合法

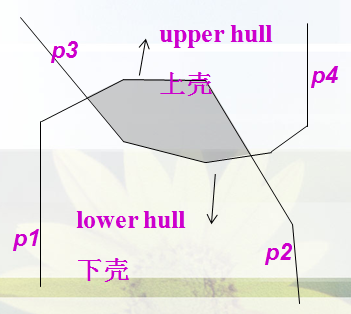
step4

现在队列中的相邻半平面的交点即为凸包的节点, 如果剩余半平面数量小于3则无解

Code(POJ2451)

// 满足Plane a的点为a.s->a.t的逆时针方向
#include <algorithm>
#include <cmath>
#include <cstdio>
#include <iomanip>
#include <iostream>

using namespace std;

inline char nc()
{
    return getchar();
    static char buf[100000], * l = buf, * r = buf;
    if(l == r) r = (l = buf) + fread(buf, 1, 100000, stdin);
    if(l == r) return EOF;
    return *l++;
}
template<class T> void readin(T & x)
{
    x = 0; int f = 1, ch = nc();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=nc();}
    while(ch>='0'&&ch<='9'){x=x*10-'0'+ch;ch=nc();}
    x *= f;
}

const double eps = 1e-9;

int sign(double a)
{
    if(fabs(a) < eps) return 0;
    return a < 0 ? -1 : 1;
}

struct Point
{
    double x, y;
    Point(double x = 0, double y = 0) : x(x), y(y) {}
};
inline Point operator + (const Point & a, const Point & b)
{
    return Point(a.x + b.x, a.y + b.y);
}
inline Point operator - (const Point & a, const Point & b)
{
    return Point(a.x - b.x, a.y - b.y);
}
inline Point operator * (const Point & a, const double & b)
{
    return Point(a.x * b, a.y * b);
}
inline double cross(Point a, Point b)
{
    return a.x * b.y - a.y * b.x;
}
inline double angle(Point a)
{
    return atan2(a.y, a.x);
}
inline bool parallel(Point p0, Point p1, Point q0, Point q1)
{
    return sign(cross(p1 - p0, q1 - q0)) == 0;
}
inline Point intersection(Point p0, Point p1, Point q0, Point q1)
{
    return p0 + (p1 - p0) * (cross(q1 - q0, p0 - q0) / cross(p1 - p0, q1 - q0));
}
inline double area(Point * p, int n)
{
    double res = 0;
    p[n + 1] = p[1];
    for(int i = 1; i <= n; i++)
    {
        res += cross(p[i], p[i + 1]);
    }
    return fabs(res / 2);
}

struct Plane
{
    Point s, t;
    double ang;
    Plane() {}
    Plane(Point s, Point t) : s(s), t(t)
    {
        ang = angle(t - s);
    }
};
inline bool operator < (const Plane & a, const Plane & b)
{
    double r = a.ang - b.ang;
    if(sign(r) != 0) return sign(r) == -1;
    return sign(cross(a.t - a.s, b.t - a.s)) == -1;
}
inline Point intersection(Plane a, Plane b)
{
    return intersection(a.s, a.t, b.s, b.t);
}
inline bool parallel(Plane a, Plane b)
{
    return parallel(a.s, a.t, b.s, b.t);
}
inline bool invalid(Plane p, Point q)
{
    return sign(cross(p.t - p.s, q - p.s)) == -1;
}
bool SI(Plane * l, int n, Point * s, int & m)
{
    static Plane q[20050];
    static Point p[20050];
    int hd = 0, tl = 0;
    sort(l + 1, l + n + 1);
    q[0] = l[1];
    for(int i = 2; i <= n; i++) if(sign(l[i].ang - l[i - 1].ang) != 0)
    {
        if(hd < tl && (parallel(q[hd], q[hd + 1]) || parallel(q[tl], q[tl - 1])))
        {
            return false;
        }
        while(hd < tl && invalid(l[i], p[tl - 1])) tl--;
        while(hd < tl && invalid(l[i], p[hd])) hd++;
        q[++tl] = l[i];
        if(hd < tl) p[tl - 1] = intersection(q[tl], q[tl - 1]);
    }
    while(hd < tl && invalid(q[hd], p[tl - 1])) tl--;
    while(hd < tl && invalid(q[tl], p[hd])) hd++;
    if(tl - hd <= 1) return false;
    p[tl] = intersection(q[hd], q[tl]);
    m = 0;
    for(int i = hd; i <= tl; i++)
    {
        s[++m] = p[i];
    }
    return true;
}

const int board = 10000;
int n, m;
Point p[20050];
Plane l[20050];

double solve()
{
    Point a = Point(0, 0);
    Point b = Point(board, 0);
    Point c = Point(board, board);
    Point d = Point(0, board);
    l[++n] = Plane(a, b);
    l[++n] = Plane(b, c);
    l[++n] = Plane(c, d);
    l[++n] = Plane(d, a);
    if(!SI(l, n, p, m)) return 0;
    return area(p, m);
}
int main()
{
    cout << fixed;
    readin(n);
    for(int i = 1; i <= n; i++)
    {
        Point p0, p1;
        scanf("%lf%lf%lf%lf", & p0.x, & p0.y, & p1.x, & p1.y);
        l[i] = Plane(p0, p1);
    }
    cout << setprecision(1) << solve() << endl;
    return 0;
}