loj 2719 [NOI2018]冒泡排序

loj 2719 [NOI2018]冒泡排序

https://loj.ac/problem/2719

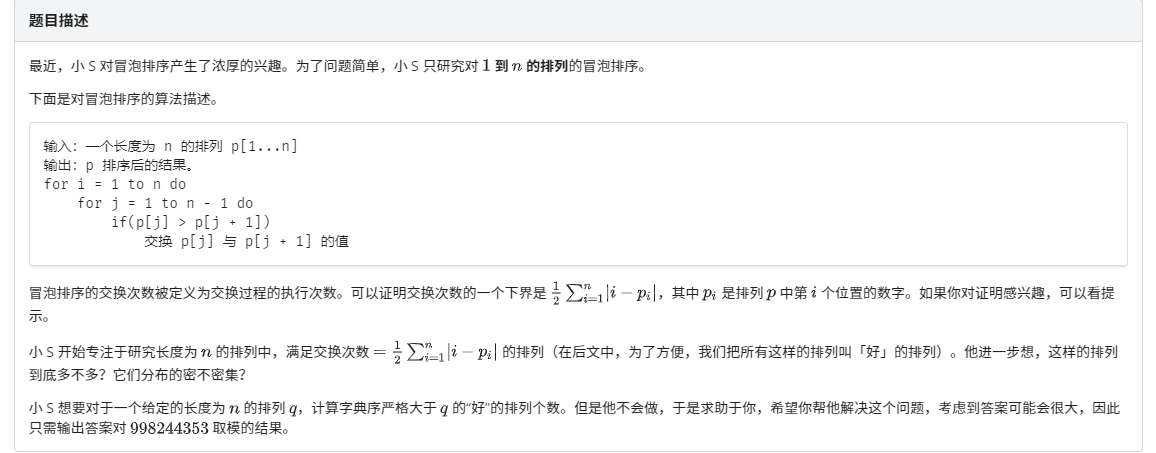
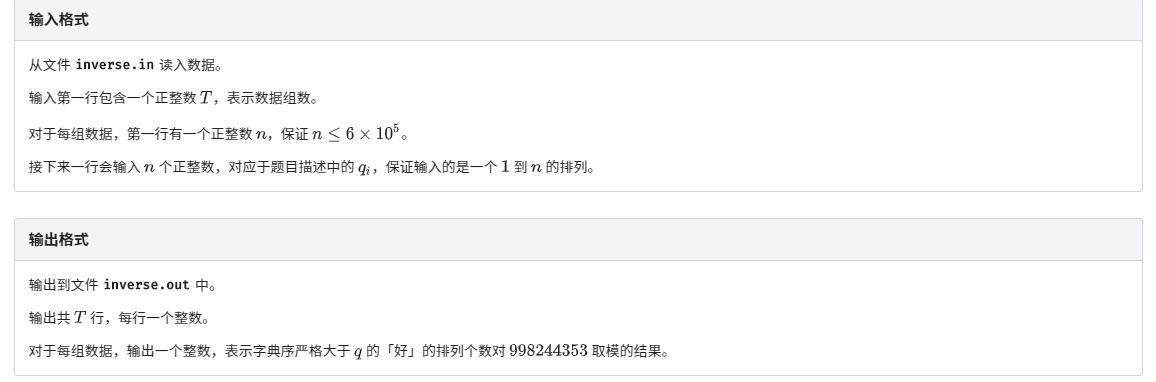
\(T =5,\sum n \le 2000000\)

Tutorial

https://www.cnblogs.com/Dance-Of-Faith/p/9339572.html

考虑什么样的排列是好的.为了达到下界,\(p_i\)应该只向\(i\)的方向移动,也就是说,不存在一个数左右都有逆序对,也就是说,不存在\(a<b<c\)使得\(p_a>p_b>p_c\)

无视\(q\)的限制,可以用DP计算答案,设\(dp(i,j)\)表示确定了排列的前\(i\)个数,设其中最大值为\(mx\),小于\(mx\)的值中有\(j\)个还没有在排列中出现.那么每次要么选择一个大于\(mx\)的数,要么将小于\(mx\)的最小的数加入排列

\[f(i,j)=f(i-1,j+1)+\sum_{k \ge 0} f(i-1,j-k) \]

初始状态为\(dp(0,0)=1\),最终答案为\(dp(n,0)\).那么考虑括号序来表示,每次\(j\)要么\(-1\),要么增加一个非负整数,那么可以看作加入任意多个左括号后加入一个右括号(\(-1\)相当于加入0个左括号).

考虑\(q\)的限制,我们可以像数位DP一样枚举\(p\)在哪个位置字典序第一次大于\(q\).那么我们可以维护在这个位置之前加入的左括号数.为了使这个位置的数大于\(q_i\),还需要加入适量左括号.于是我们要计算的就是,当前序列有\(cnt\)个左括号,还可以加入\(n-i+1\)个右括号,其中每个右括号前可以增加任意个左括号,这样的合法括号序个数.

设当前有\(b\)个左括号,还可以加入\(a\)个右括号,那么一共要加入的括号数就是\(n=2a-b\).考虑折线法,翻转第一次到达\(y=-1\)直线之前的路径,那么所有非法路径相当于从\((0,-y-2)\)到\((n,0)\)的路径数.那么答案相当于

\[\binom nx - \binom n{y+2+\dfrac {n-y-2}2} = \binom nx - \binom n{\dfrac {n+y}2+1} \]

注意在枚举字典序第一次大于的位置时注意已经加入的部分是否合法.

Code

#include <cstdio>
#include <cstring>
#include <iostream>
#define debug(...) fprintf(stderr,__VA_ARGS__)
#define inver(a) power(a,mod-2)
using namespace std;
inline char nc() {
	static char buf[100000],*l=buf,*r=buf;
	return l==r&&(r=(l=buf)+fread(buf,1,100000,stdin),l==r)?EOF:*l++;
} 
template<class T> void read(T &x) {
	x=0; int f=1,ch=nc();
	while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=nc();}
	while(ch>='0'&&ch<='9'){x=x*10-'0'+ch;ch=nc();}
	x*=f;
}
typedef long long ll;
const int mod=998244353;
const int maxn=6e5+50;
int T,n,q[maxn];
int fac[maxn<<1],inv[maxn<<1];
bool vis[maxn];
inline int add(int x) {return x>=mod?x-mod:x;}
inline int sub(int x) {return x<0?x+mod:x;}
ll power(ll x,ll y) {
	ll re=1;
	while(y) {
		if(y&1) re=re*x%mod;
		x=x*x%mod;
		y>>=1;
	}
	return re;
}
inline int binom(int x,int y) {
	if(x<y) return 0;
	return (ll)fac[x]*inv[y]%mod*inv[x-y]%mod;
}
inline int cal(int x,int y) {
	int n=x*2-y;
	return sub(binom(n,x)-binom(n,(n+y)/2+1));
}
void init(int n) {
	fac[0]=1;
	for(int i=1;i<=n;++i) fac[i]=(ll)fac[i-1]*i%mod;
	inv[n]=inver(fac[n]);
	for(int i=n;i>=1;--i) inv[i-1]=(ll)inv[i]*i%mod;
} 
int main() {
	freopen("inverse.in","r",stdin);
	freopen("inverse.out","w",stdout);
	init(12e5);
	read(T);
	for(int kase=1;kase<=T;++kase) {
		read(n);
		for(int i=1;i<=n;++i) read(q[i]);
		int mx=0,mn=1,cnt=0,an=0;
		memset(vis,0,sizeof(vis));
		for(int i=1;i<=n;++i,--cnt) {
			if(mx<q[i]) cnt+=q[i]-mx,mx=q[i];
			an=add(an+cal(n-i+1,cnt+1));
			vis[q[i]]=1; while(vis[mn]) ++mn;
			if(mx>q[i]&&q[i]>mn) break;
		}
		printf("%d\n",an);
	}
	return 0;
}