agc030_e Less than 3
agc030_e Less than 3
https://atcoder.jp/contests/agc030/tasks/agc030_e
Tutorial
https://img.atcoder.jp/agc030/editorial.pdf
观察一次操作进行的条件.
假如要对位置\(x\)进行操作,那么\(x-1,x+1\)的字符就必须不同,否则在操作前或后是不合法的.
所以除非在边界操作,01的联通块顺序和数量是不会改变的.
我们在01之间插入红色隔板,在10之间插入蓝色隔板,得到
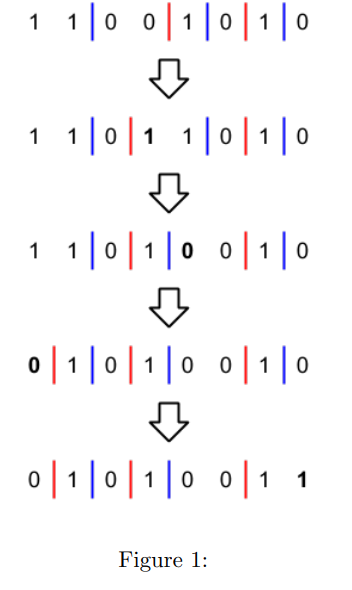
对于边界的情况,我们可以假设左右边界外分别有无限多隔板,且满足红蓝交替出现
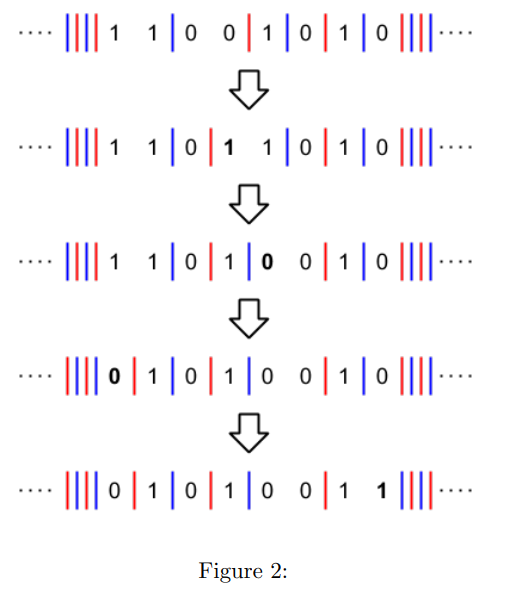
由此我们可以将问题转化为
- 有若干个隔板,除了两个在边界的隔板之外,任何隔板之间的距离只能为\(1\)或\(2\).且红蓝交替出现.
- 一次操作可以将某个隔板向前或向后移动\(1\),且不改变相对位置,且移动后仍满足上述条件
我们可以对于\(s,t\)之间的隔板建立对应关系,则答案下界为对应隔板之间的距离和.
考虑这个下界是否总是可以达到,我们将隔板按照与其对应隔板的位置关系分为"向左,向右,不动"3类.由于隔板之间的距离为\(1,2\)且顺序不改变,所以没有向右和向左的隔板相邻,所以一定是形如"向右,向右,不动,向左,向左,不动"这样的顺序.观察发现一个向左或向右连续段里面总有一个隔板可以向目标位置移动.
所以我们枚举对应关系即可,最多有\(1\)个左边界的隔板与右边界的隔板对应,所以一共有\(O(n)\)种对应关系,时间复杂度\(O(n^2)\)
Code
#include <cmath>
#include <cstdio>
#include <iostream>
#include <vector>
#define debug(...) fprintf(stderr,__VA_ARGS__)
#define fi first
#define se second
using namespace std;
template<class T> void rd(T &x) {
x=0; int f=1,ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10-'0'+ch;ch=getchar();}
x*=f;
}
template<class T> inline bool Cmin(T &x,T y) {return x>y?x=y,1:0;}
const int inf=1e9;
const int maxn=5000+5;
int n; char s[maxn],t[maxn];
vector< pair<int,int> > S,T;
int sol(int a,int b) {
int an=0;
while(S[a].fi!=n||T[b].fi!=n) an+=abs(S[a++].fi-T[b++].fi);
return an;
}
void init(char *s,vector< pair<int,int> > &S) {
for(int i=0;i<n;++i) S.push_back(make_pair(0,i&1));
if((n&1)==(s[1]=='1')) S.push_back(make_pair(0,n&1));
for(int i=1;i<n;++i) if(s[i]!=s[i+1]) {
int c=S.back().se^1;
S.push_back(make_pair(i,c));
}
for(int i=0;i<2*n;++i) {
int c=S.back().se^1;
S.push_back(make_pair(n,c));
}
}
int main() {
rd(n);
scanf("%s",s+1);
scanf("%s",t+1);
init(s,S),init(t,T);
int an=inf;
for(int i=0;i<=n;++i) if(S[i].se==T[n].se) Cmin(an,sol(i,n));
for(int i=0;i<=n;++i) if(S[n].se==T[i].se) Cmin(an,sol(n,i));
printf("%d\n",an);
return 0;
}





