CodeForces 1268E Happy Cactus

CodeForces 1268E Happy Cactus

https://codeforces.com/contest/1268/problem/E

\(n\) 个点 \(m\) 条边的仙人掌.(\(1 \le n,m \le 500000\)) 其中第 \(i\) 条边的边权为 \(i\)

称 \((u,v)\) 的路径是happy若这条路径上的边的边权是递增的.

对于每个点 \(u\) ,求有多少个点 \(v(u \not= v)\) 满足 \((u,v)\) 是happy的.

Tutorial

考虑如果这是树上怎么做.

设 \(dp_u\) 表示 \(u\) 节点此时的答案.

从大到小加入每条边 \((a,b)\) ,则其他点答案不变, \(dp_a,dp_b\) 变为 \(dp_a+dp_b\) .

可以看作有每个节点上有一只老鼠,第 \(i\) 个节点上的老鼠有第 \(i\) 种疾病,每次 \(a,b\) 节点的老鼠会将自己身上的疾病传染给彼此.

回到仙人掌上.

假如 \(a,b\) 当前在不同联通块中,那么与树类似

否则,若 \(a,b\) 当前在同一联通块中,那么它们身上的疾病就可能存在交集,观察

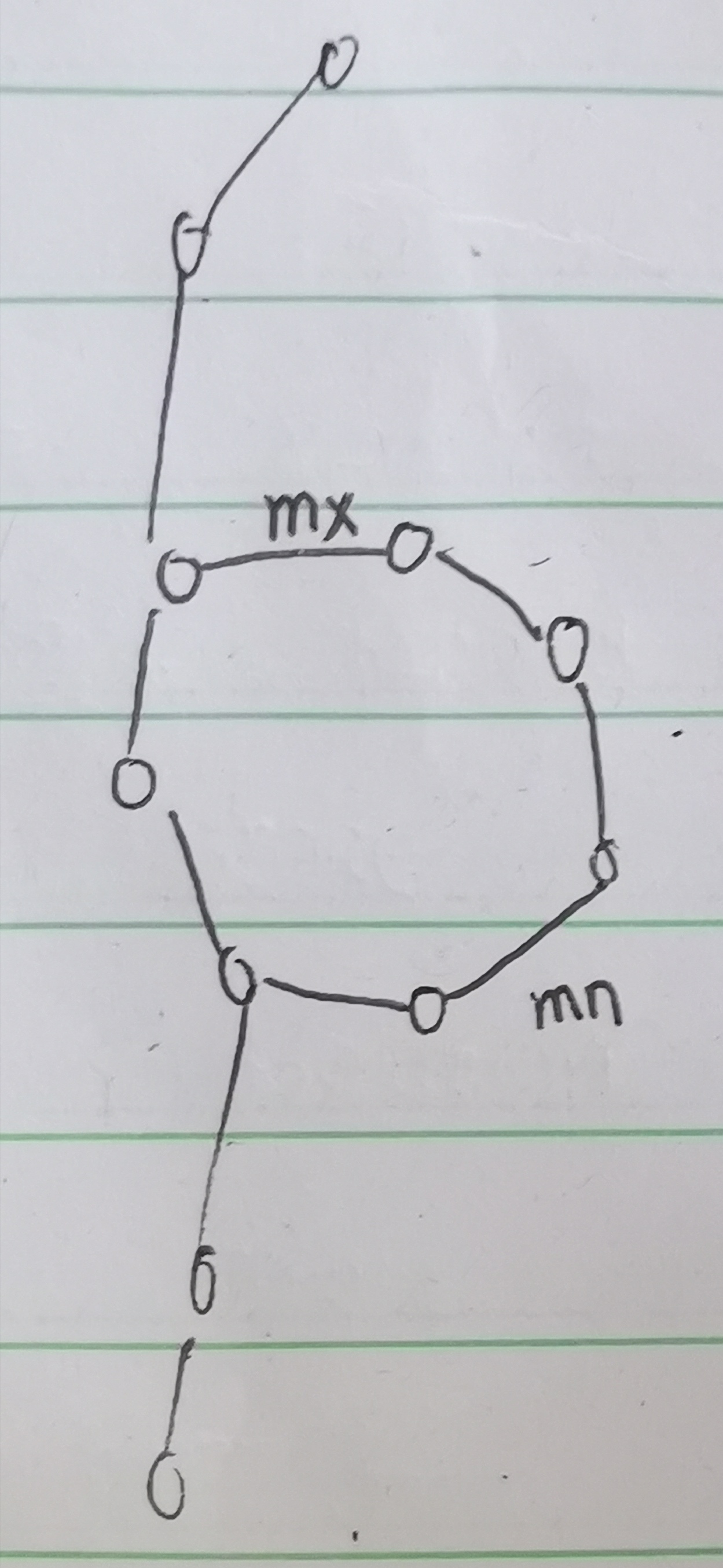
其中 \(mn\) 是当前枚举的边, \(mx\) 是 \(mn\) 所在环中边权最大的边.

发现当且仅当mx到mn的两条路径的边权都是递减的时候,mx所传染的疾病才会成为 \(a,b\) 疾病的交集.

设在枚举第 \(i\) 条边时, \(f_i=dp_a+dp_b\) .则此时 \(f_{mn}=dp_a+dp_b-f_{mx}\)

Code

#include <cassert>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <vector>
#define debug(...) fprintf(stderr,__VA_ARGS__)
using namespace std;
inline char nc()
{
    static char buf[100000],*l=buf,*r=buf;
    return l==r&&(r=(l=buf)+fread(buf,1,100000,stdin),l==r)?EOF:*l++;
}
template<class T> void read(T &x)
{
    x=0; int f=1,ch=nc();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=nc();}
    while(ch>='0'&&ch<='9'){x=x*10-'0'+ch;ch=nc();}
    x*=f;
}
template<class T> inline bool Cmax(T &x,T y) {return x<y?x=y,1:0;}
template<class T> inline bool Cmin(T &x,T y) {return x>y?x=y,1:0;}
const int inf=1e9;
const int maxn=500000+50;
const int maxm=500000+50;
int m;
int n;
int dfc;
int a[maxm];
int b[maxm];
int e[maxm];
int f[maxm];
int dp[maxn];
int anc[maxn];
int dfn[maxn];
int pre[maxn];
int head[maxn];
struct edge
{
    int to,nex,id;
    edge(int to=0,int nex=0,int id=0):to(to),nex(nex),id(id){}
};
vector<edge> G;
inline void addedge(int u,int v,int id)
{
    G.push_back(edge(v,head[u],id)),head[u]=G.size()-1;
    G.push_back(edge(u,head[v],id)),head[v]=G.size()-1;
}
namespace us
{
    int fa[maxn];
    void init(int n)
    {
        for(int i=1;i<=n;++i) fa[i]=i;
    }
    int find(int a) {return a==fa[a]?a:fa[a]=find(fa[a]);}
    inline bool merge(int a,int b)
    {
        a=find(a),b=find(b);
        if(a==b) return 0;
        fa[a]=b; return 1;
    }
}
void dfs(int u)
{
    dfn[u]=++dfc;
    for(int i=head[u];~i;i=G[i].nex)
    {
        int v=G[i].to; if(v==anc[u]) continue;
        if(!dfn[v])
        {
            anc[v]=u;
            pre[v]=G[i].id;
            dfs(v);
        }
        else if(dfn[v]<dfn[u])
        {
            vector<int> C;
            C.push_back(G[i].id);
            for(int x=u;x!=v;x=anc[x])
            {
                C.push_back(pre[x]);
            }
            int n=C.size();
            int mn=inf,mx=-inf,mxp,mnp;
            for(int i=0;i<n;++i)
            {
                if(Cmin(mn,C[i])) mnp=i;
                if(Cmax(mx,C[i])) mxp=i;
            }
            // debug("%d %d\n",mn,mx);
            bool ok=1;
            for(int i=mxp,j;i!=mnp;i=j)
            {
                j=i==n-1?0:i+1;
                if(C[i]<C[j]) {ok=0; break;}
            }
            for(int i=mxp,j;i!=mnp;i=j)
            {
                j=i==0?n-1:i-1;
                if(C[i]<C[j]) {ok=0; break;}
            }
            if(ok) e[mn]=mx;
        }
    }
}
int main()
{
    // freopen("in.txt","r",stdin);
    // freopen("out.txt","w",stdout);
    read(n),read(m);
    memset(head,-1,sizeof(head));
    for(int i=1;i<=m;++i)
    {
        read(a[i]),read(b[i]);
        addedge(a[i],b[i],i);
    }
    dfs(1);
    us::init(n);
    for(int i=1;i<=n;++i) dp[i]=1;
    for(int i=m;i>=1;--i)
    {
        int re=dp[a[i]]+dp[b[i]];
        if(!us::merge(a[i],b[i]))
        {
            if(e[i]) re-=f[e[i]];
        }
        dp[a[i]]=dp[b[i]]=f[i]=re;
        // for(int j=1;j<=n;++j) debug("%d ",dp[j]); debug("\n");
    }
    for(int i=1;i<=n;++i)
    {
        if(i!=1) printf(" ");
        printf("%d",dp[i]-1);
    }
    printf("\n");
    return 0;
}