[洛谷 P3713] [BJOI2017]机动训练

[BJOI2017]机动训练

参考博客

https://www.luogu.org/problemnew/solution/P3713

洛谷 P3713

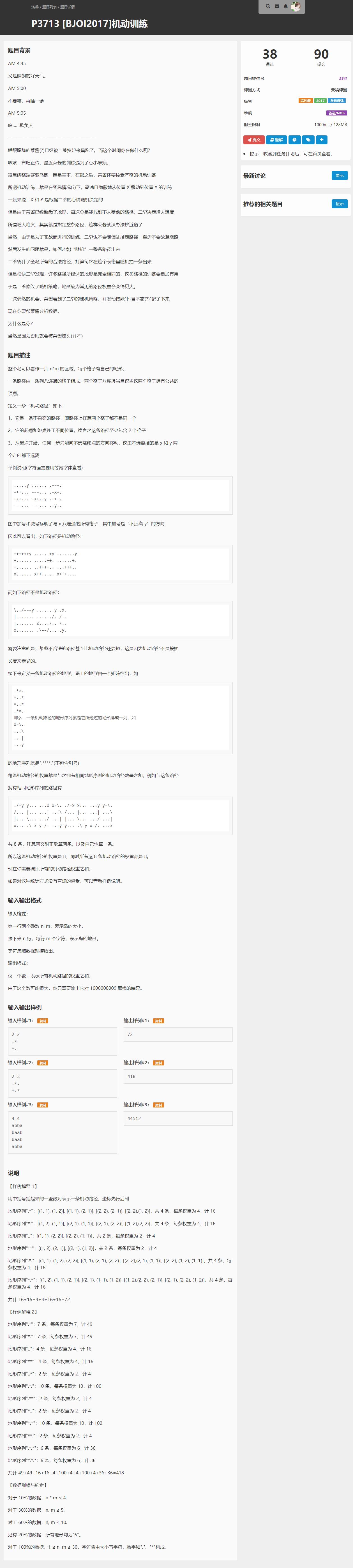
题目大意

有一张 \(n \times m\) 的网格图，每个格子上有一个字符，一个格子是八联通的，定义一条路径

1. 选定起点 \(s\) ，终点 \(t\) ，\(s \not= t\)
2. 设一步后从 \((x, y)\) 走到了 \((x', y')\) 那么 \(|tx - x| \ge |tx - x'|, |ty - y| \ge |ty - y'|\)
3. 将经过格子上的字符连成一个字符串，则这条路径的种类可以被表示为这个字符串

问每种路径的个数的平方之和

数据范围

\(1 \le n,m \le 30\)

时空限制

1000ms, 128MB

分析

一个人出发每种类的方案平方和，从组合意义上可以转化为两个人出发走相同路径的方案数。。。。

容斥计算答案，通过一些剪枝减少dp次数

Code

#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
template<class T> void read(T &x) {
	x = 0; int f = 1, ch = getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
	while(ch>='0'&&ch<='9'){x=x*10-'0'+ch;ch=getchar();}
	x *= f;
}
#define judge(x, y) ((x) > 0 && (x) <= n && (y) > 0 && (y) <= m)
#define rev(x) ((x) < 4 ? 3 - (x) : 11 - (x))
const int mod = 1000000009;
const int maxn = 30 + 5;
const int maxm = 30 + 5;
int n, m; char s[maxn][maxm];
int n1, n2, d1[8][2], d2[8][2];
bool vis[maxn][maxm][maxn][maxm];
int f[maxn][maxm][maxn][maxm], g[8][8];
inline void add(int &x, int y) {
	x += y; 
	if(x >= mod) x -= mod;
	if(x < 0) x += mod;
}
void process(int d[8][2], int &n, int k) {
	const int t[8][8][2] = {
	{{0, -1}, {-1, -1}, {-1, 0}},
	{{-1, 0}, {-1, 1}, {0, 1}},
	{{1, 0}, {1, -1}, {0, -1}},
	{{0, 1}, {1, 1}, {1, 0}},
	{{0, -1}}, {{-1, 0}}, {{1, 0}}, {{0, 1}}};
	n = k < 4 ? 3 : 1;
	memcpy(d, t[k], sizeof(t[k]));
}
int dp(int a, int b, int c, int d) {
	if(vis[a][b][c][d]) return f[a][b][c][d];
	vis[a][b][c][d] = 1;
	int & re = f[a][b][c][d] = 1;
	for(int i = 0; i < n1; ++i) {
		int _a = a + d1[i][0];
		int _b = b + d1[i][1];
		if(!judge(_a, _b)) continue;
		for(int j = 0; j < n2; ++j) {
			int _c = c + d2[j][0];
			int _d = d + d2[j][1];
			if(!judge(_c, _d)) continue;
			if(s[_a][_b] == s[_c][_d]) add(re, dp(_a, _b, _c, _d));
		}
	}
	return re;
}
int solve(int x, int y) {
	if(g[x][y] != -1) return g[x][y];
	int & re = g[x][y] = 0;
	process(d1, n1, x);
	process(d2, n2, y);
	memset(vis, 0, sizeof(vis));
	for(int a = 1; a <= n; ++a) {
		for(int b = 1; b <= m; ++b) {
			for(int c = 1; c <= n; ++c) {
				for(int d = 1; d <= m; ++d) if(s[a][b] == s[c][d]) {
					add(re, dp(a, b, c, d) - 1);
				}
			}
		}
	} 
	g[y][x] = g[rev(x)][rev(y)] = g[rev(y)][rev(x)] = re;
	return re;
} 
int main() {
//	freopen("testdata.in", "r", stdin);
	read(n), read(m);
	for(int i = 1; i <= n; ++i) {
		scanf("%s", s[i] + 1);
	}
	int an = 0;
	memset(g, -1, sizeof(g));
	for(int i = 0; i < 8; ++i) {
		for(int j = 0; j < 8; ++j) {
			add(an, (i < 4 ? 1 : -1) * (j < 4 ? 1 : -1) * solve(i, j));
		}
	}
	printf("%d\n", an);
	return 0;
}

总结

对平方和的转化。。。

从组合意义上思考题目