[洛谷 P3992] [BJOI2017]开车

[BJOI2017]开车

P3992

题目大意

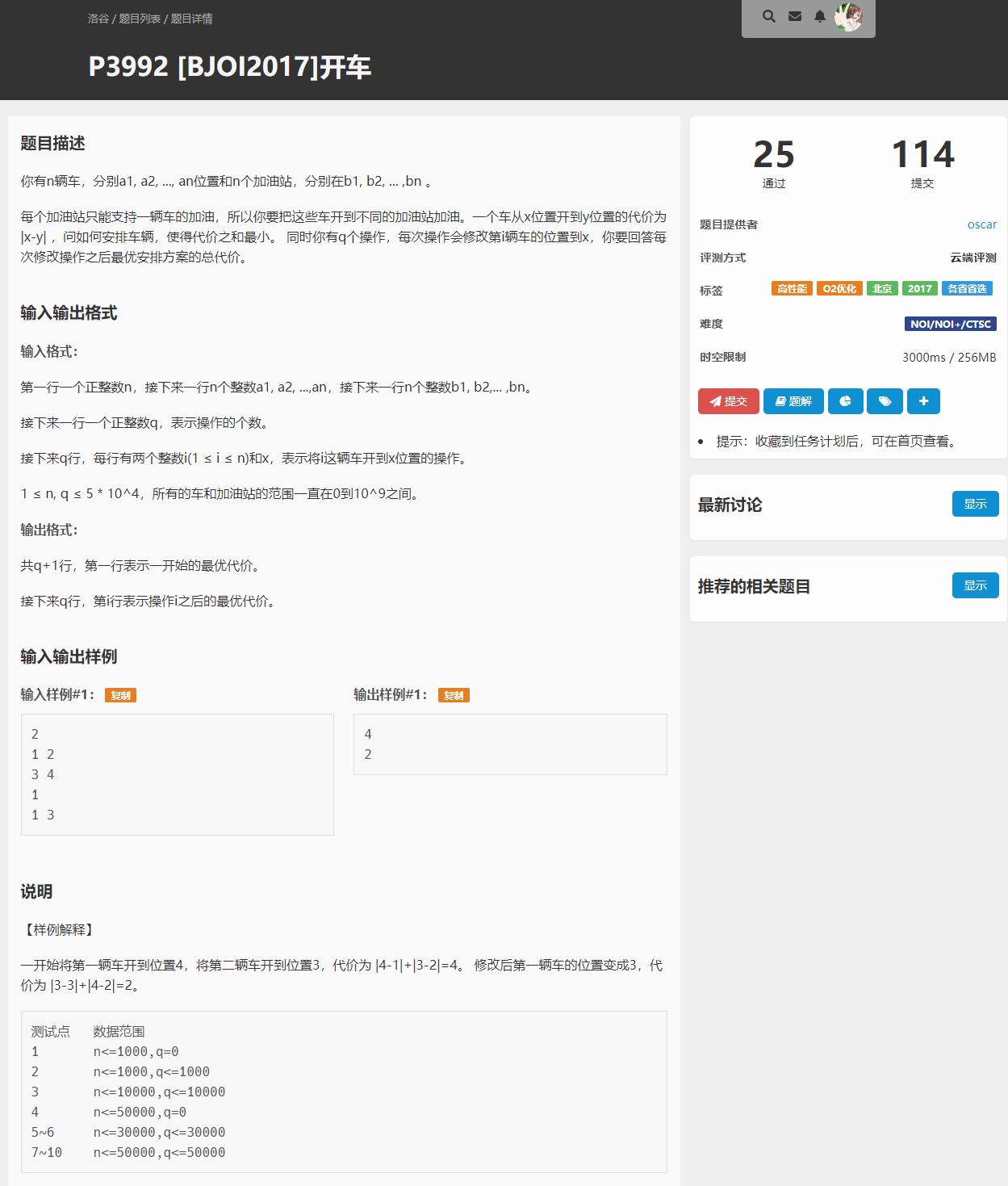
给出 \(n\) 个车的位置 \(a_i\) 和 \(n\) 个加油站的位置 \(b_i\) ，一辆车从 \(x\) 位置到 \(y\) 位置的代价为 \(|x - y|\) ，问如何两两配对使答案最小，\(q\) 次询问每次修改 \(a_x\) 为 \(y\) ，每次修改后给出当前答案。

数据范围

\(n \le 50000, q \le 50000\)

时空限制

3000ms, 256MB, O2

反思

似乎根本没有任何思考就点开了题解

分析

首先发现答案实际上就是分别排序后对应配对，考虑维护数轴上每条边的贡献，发现我们记一个 \(a_i\) 为 \(1\) ，$b_i $ 为 \(-1\) 的前缀和，那么它的贡献就是 \(|sum|\)

那么我们修改就相当于区间 \(\pm 1\) ，但是我们无法简单地维护一个绝对值，所以用分块的方法

将块内的前缀和排序，二分 \(0\) 点，带上标记即可修改

Code

#include <algorithm> 
#include <cmath>
#include <cstdio> 
#include <iostream>
using namespace std;
inline char nc() {
	static char buf[100000], *l = buf, *r = buf;
	return l==r&&(r=(l=buf)+fread(buf,1,100000,stdin),l==r)?EOF:*l++;
} 
template<class T> void read(T &x) {
	x = 0; int f = 1, ch = nc();
	while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=nc();}
	while(ch>='0'&&ch<='9'){x=x*10-'0'+ch;ch=nc();}
	x *= f;
}
#define myabs(a) ((a) < 0 ? - (a) : (a))
typedef long long ll;
const int maxn = 50000 + 5;
const int maxq = 50000 + 5;
const int maxp = maxn * 2 + maxq;
const int maxb = 400;
int n, q, a[maxn], b[maxn]; ll an;
int H[maxp], p;
struct data {
	int x, y;
} ask[maxq];
void Hash() {
	sort(H + 1, H + p + 1);
	p = unique(H + 1, H + p + 1) - H - 1;
	for(int i = 1; i <= n; ++i) {
		a[i] = lower_bound(H + 1, H + p + 1, a[i]) - H;
	}
	for(int i = 1; i <= n; ++i) {
		b[i] = lower_bound(H + 1, H + p + 1, b[i]) - H;
	}
	for(int i = 1; i <= q; ++i) {
		ask[i].y = lower_bound(H + 1, H + p + 1, ask[i].y) - H;
	}
}
namespace blocks {
	int len;
	int L[maxb], R[maxb], bel[maxp];
	int sum[maxp], val[maxp];
	int sval[maxp], ord[maxp], tag[maxb];
	inline int cmp(const int &a, const int &b) {
		return sum[a] < sum[b];
	} 
	void rebuild(int x) {
		sort(ord + L[x], ord + R[x] + 1, cmp);
		sval[L[x]] = val[ord[L[x]]];
		for(int i = L[x] + 1; i <= R[x]; ++i) {
			sval[i] = sval[i - 1] + val[ord[i]];
		}
	}
	void init() {
		for(int i = 1; i <= n; ++i) {
			sum[a[i]]++, sum[b[i]]--;
		}
		for(int i = 1; i <= p; ++i) {
			if(i < p) val[i] = H[i + 1] - H[i];
			sum[i] += sum[i - 1];
			an += (ll)myabs(sum[i]) * val[i];
		}
		len = ceil(sqrt(p));
		for(int i = 1; i <= p; ++i) {
			int x = bel[i] = (i - 1) / len + 1;
			if(!L[x]) L[x] = i;
			R[x] = i;
		}
		for(int i = 1; i <= p; ++i) ord[i] = i;
		for(int i = 1; i <= bel[p]; ++i) {
			rebuild(i);
		}
	}
	void add(int x) {
		for(int i = x; i <= R[bel[x]]; ++i) {
			an += val[i] * (sum[i] + tag[bel[x]] >= 0 ? 1 : -1);
			sum[i]++;
		}
		rebuild(bel[x]);
		for(int i = bel[x] + 1; i <= bel[p]; ++i) {
			int l = L[i], r = R[i], re = -1;
			while(l <= r) {
				int mid = (l + r) >> 1;
				if(sum[ord[mid]] + tag[i] >= 0) r = mid - 1, re = mid;
				else l = mid + 1;
			}
			if(re == -1) {
				an -= sval[R[i]];
			}
			else if(re == L[i]) {
				an += sval[R[i]];
			}
			else {
				an -= sval[re - 1];
				an += sval[R[i]] - sval[re - 1];
			}
			tag[i]++;
		}
	}
	void sub(int x) {
		for(int i = x; i <= R[bel[x]]; ++i) {
			an += val[i] * (sum[i] + tag[bel[x]] <= 0 ? 1 : -1);
			sum[i]--;
		}
		rebuild(bel[x]);
		for(int i = bel[x] + 1; i <= bel[p]; ++i) {
			int l = L[i], r = R[i], re = -1;
			while(l <= r) {
				int mid = (l + r) >> 1;
				if(sum[ord[mid]] + tag[i] <= 0) l = mid + 1, re = mid;
				else r = mid - 1;
			}
			if(re == -1) {
				an -= sval[R[i]];
			}
			else if(re == R[i]) {
				an += sval[R[i]];
			}
			else {
				an += sval[re];
				an -= sval[R[i]] - sval[re];
			}
			tag[i]--;
		}
	}
}
int main() {
//	freopen("testdata.in", "r", stdin);
//	freopen("testdata.out", "w", stdout); 
	read(n);
	for(int i = 1; i <= n; ++i) {
		read(a[i]), H[++p] = a[i];
	}
	for(int i = 1; i <= n; ++i) {
		read(b[i]), H[++p] = b[i];
	}
	read(q); 
	for(int i = 1; i <= q; ++i) {
		read(ask[i].x), read(ask[i].y);
		H[++p] = ask[i].y;
	}
	Hash();
	blocks :: init();
	printf("%lld\n", an);
	for(int i = 1; i <= q; ++i) {
		int x = ask[i].x, y = ask[i].y;
		blocks :: sub(a[x]);
		blocks :: add(a[x] = y);
		printf("%lld\n", an);
	}
	return 0;
}

总结

利用分块维护绝对值