数据结构与算法——弗洛伊德(Floyd)算法
介绍
和 Dijkstra 算法一样,弗洛伊德(Floyd)算法 也是一种用于寻找给定的加权图中顶点间最短路径的算法。该算法名称以创始人之一、1978 年图灵奖获得者、斯坦福大学计算机科学系教授罗伯特·弗洛伊德命名
弗洛伊德算法(Floyd)计算图中 各个顶点之间 的最短路径,比如:先从 A 出发到各个点的最短路径,再从 B 出发,直到所有节点距离各个点的路径都会计算出来。而迪杰斯特拉算法用于计算图中 某一个顶点到其他顶点的最短路径。
弗洛伊德算法 VS 迪杰斯特拉算法:
- 迪杰斯特拉算法通过选定的被访问顶点,求出从出发访问顶点到其他顶点的最短路径;(关于Dijkstra 算法可以看 数据结构与算法——迪杰斯特拉算法)
- 弗洛伊德算法中每一个顶点都是出发访问点,所以需要将每一个顶点看做被访问顶点,求出从每一个顶点到其他顶点的最短路径。
核心思想
设:
- 顶点 vi 到顶点 vk 的最短路径已知为Lik,
- 顶点 vk 到 vj 的最短路径已知为 Lkj
- 顶点 vi 到 vj 的路径为 Lij
则 vi 到 vj 的最短路径为:min((Lik+Lkj),Lij),vk 的取值为图中所有顶点,则可获得 vi 到 vj 的最短路径(则:假设三个点(不一定是具体的是 3 个点),一个直达,一个间接到达,算哪个路径最短)
至于 vi 到 vk 的最短路径 Lik 或者 vk 到 vj 的最短路径 Lkj,是以同样的方式获得
图解
以前面的公交站距离图解

上图中含义:
- 0:表示自己与自己。如 A,A
- N:表示不可直连

初始前驱顶点如上图:每个节点到达其他节点的初始前驱都是它自己。
-
第一轮循环中,以 A (下标为:0) 作为 中间顶点,距离表和前驱关系更新为:
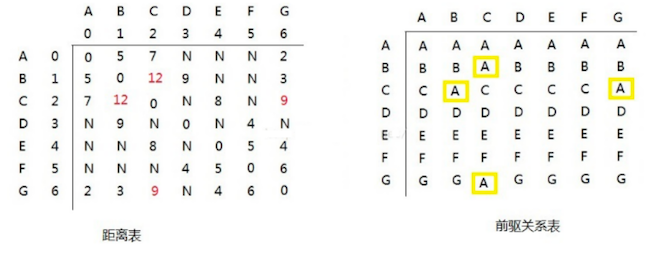
-
找出以 A 为中间顶点的路径:
C-A-G:距离为 9C-A-B:距离为 12G-A-B:距离为 7
因为图是无向的,只需要计算一个方向的即可。
-
更新距离表,需要与上一次的距离表作为参照对比
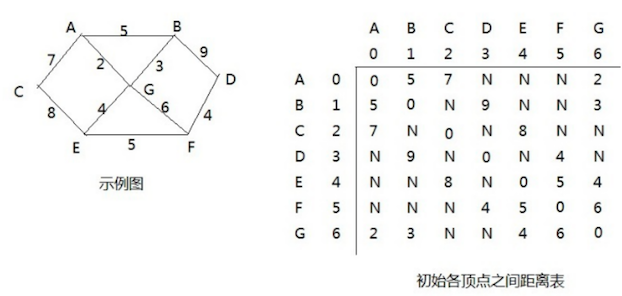
C-A-G:距离为 9,原始C,G距离为 N,9 < N,则更新C,G = 9C-A-B:距离为 12,原始C,B距离为 N,12 < N,则更新C,B=12G-A-B:距离为 7,原始G,B距离为 3,则不更新
另外由于是无向图,更新其中一个,那么另外一个方向的也要同步更新。
同时:更新对应位置的前驱节点为 A
-
如何找出以 A 为中间顶点的所有路径?
// 使用 3 个数组来实现,思路如下 中间顶点:[A,B,C,D,E,F,G] k=0 出发顶点:[A,B,C,D,E,F,G] i=0,1.... 终点顶点:[A,B,C,D,E,F,G] j=0,1,2... 以 k 为中间顶点时,使用一个双层循环,来遍历出所有的情况 并在这个寻找路径的循环中,找出最短路径,去更新上述所演示的:距离表、前驱表当把 A 作为中间顶点路径寻找完成之后,表中的数据则为 A 到所有顶点的最短距离。
当所有顶点都更新之后,最后就是每个顶点到其他顶点的最短距离(注:所有顶点没有更新完成之前,最终结果不一定是最短的,后续可能还会更新)
看上去很简单,就是一个三层 for 循环,但是它的时间复杂度是 n3,比如这里有 7 个节点,那么循环的次数是
7x7x7=343
-
弗洛伊德算法最佳应用-最短路径
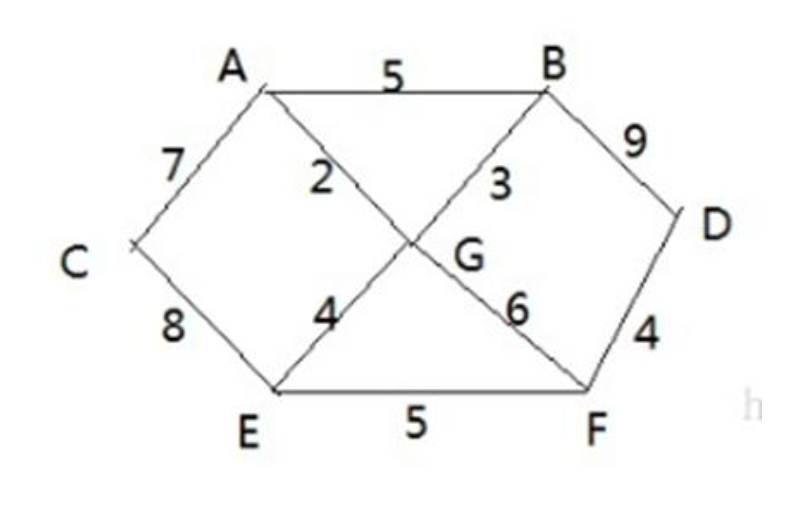
胜利乡有 7 个村庄 (A, B, C, D, E, F, G),各个村庄的距离用边线表示(权),比如 A-B 距离为 5 公里
问:如何计算出 各村庄到其他各村庄的最短距离?
下面直接用代码实现,前面图解和思路都说了。
准备工作
主要做了 3 件事情:
- 复用了之前的无向图和打印功能
- 初始化弗洛伊德算法中用到的 3 个数组和初始化
- 打印状态和结果
/**
* 佛洛依德算法-最短路径
*/
public class FloydAlgorithm {
/**
* 图:首先需要有一个带权的连通无向图
*/
class MGraph {
int vertex; // 顶点个数
int[][] weights; // 邻接矩阵
char[] datas; // 村庄数据
/**
* @param vertex 村庄数量, 会按照数量,按顺序生成村庄,如 A、B、C...
* @param weights 需要你自己定义好那些点是连通的,那些不是连通的
*/
public MGraph(int vertex, int[][] weights) {
this.vertex = vertex;
this.weights = weights;
this.datas = new char[vertex];
for (int i = 0; i < vertex; i++) {
// 大写字母 A 从 65 开始
datas[i] = (char) (65 + i);
}
}
public void show() {
System.out.printf("%-8s", " ");
for (char vertex : datas) {
// 控制字符串输出长度:少于 8 位的,右侧用空格补位
System.out.printf("%-8s", vertex + " ");
}
System.out.println();
for (int i = 0; i < weights.length; i++) {
System.out.printf("%-8s", datas[i] + " ");
for (int j = 0; j < weights.length; j++) {
System.out.printf("%-8s", weights[i][j] + " ");
}
System.out.println();
}
}
}
@Test
public void mGraphTest() {
// 不连通的默认值:
// 这里设置为较大的数,是为了后续的计算方便,计算权值的时候,不会选择
int defaultNo = 100000;
int[][] weights = new int[][]{
{defaultNo, 5, 7, defaultNo, defaultNo, defaultNo, 2}, // A
{5, defaultNo, defaultNo, 9, defaultNo, defaultNo, 3},// B
{7, defaultNo, defaultNo, defaultNo, 8, defaultNo, defaultNo},// C
{defaultNo, 9, defaultNo, defaultNo, defaultNo, 4, defaultNo},// D
{defaultNo, defaultNo, 8, defaultNo, defaultNo, 5, 4},// E
{defaultNo, defaultNo, defaultNo, 4, 5, defaultNo, 6},// F
{2, 3, defaultNo, defaultNo, 4, 6, defaultNo}// G
};
MGraph mGraph = new MGraph(7, weights);
mGraph.show();
}
@Test
public void floydTest() {
int defaultNo = 100000;
int[][] weights = new int[][]{
{defaultNo, 5, 7, defaultNo, defaultNo, defaultNo, 2}, // A
{5, defaultNo, defaultNo, 9, defaultNo, defaultNo, 3},// B
{7, defaultNo, defaultNo, defaultNo, 8, defaultNo, defaultNo},// C
{defaultNo, 9, defaultNo, defaultNo, defaultNo, 4, defaultNo},// D
{defaultNo, defaultNo, 8, defaultNo, defaultNo, 5, 4},// E
{defaultNo, defaultNo, defaultNo, 4, 5, defaultNo, 6},// F
{2, 3, defaultNo, defaultNo, 4, 6, defaultNo}// G
};
MGraph mGraph = new MGraph(7, weights);
mGraph.show();
floyd(mGraph);
showFloydDis();
showFloydPre();
showFormat();
}
//弗洛伊德算法中用到的 3 个数组
private char[] vertexs; // 存放顶点
private int[][] dis; // 从各个顶点出发到其他顶点的距离
private int[][] pre; // 到达目标顶点的前驱顶点
//这里的代码还没有写完,缺少算法的核心代码
public void floyd(MGraph mGraph) {
vertexs = mGraph.datas;
dis = mGraph.weights;
pre = new int[mGraph.vertex][mGraph.vertex];
// 初始化 pre
for (int i = 0; i < pre.length; i++) {
Arrays.fill(pre[i], i);
}
}
/**
* 显示 dis 和 pre,这个数据也是最后的结果数据
*/
public void showFloydDis() {
System.out.println("dis 结果");
show(dis);
}
public void showFloydPre() {
System.out.println("pre 结果");
show(pre);
}
public void show(int[][] weights) {
System.out.printf("%-8s", " ");
for (char vertex : vertexs) {
// 控制字符串输出长度:少于 8 位的,右侧用空格补位
System.out.printf("%-8s", vertex + " ");
}
System.out.println();
for (int i = 0; i < weights.length; i++) {
System.out.printf("%-8s", vertexs[i] + " ");
for (int j = 0; j < weights.length; j++) {
System.out.printf("%-8s", weights[i][j] + " ");
}
System.out.println();
}
}
/**
* 直接打印出我们的结果
*/
public void showFormat() {
System.out.println("最终结果格式化显示:");
for (int i = 0; i < dis.length; i++) {
// 先将 pre 数组输出一行
System.out.println(vertexs[i] + " 到其他顶点的最短距离");
// 输出 dis 数组的一行数据
// 每一行数据是,一个顶点,到达其他顶点的最短路径
for (int k = 0; k < dis.length; k++) {
System.out.printf("%-16s", vertexs[i] + " → " + vertexs[k] + " = " + dis[i][k] + "");
}
System.out.println();
System.out.println();
}
}
}
测试输出
A B C D E F G
A 100000 5 7 100000 100000 100000 2
B 5 100000 100000 9 100000 100000 3
C 7 100000 100000 100000 8 100000 100000
D 100000 9 100000 100000 100000 4 100000
E 100000 100000 8 100000 100000 5 4
F 100000 100000 100000 4 5 100000 6
G 2 3 100000 100000 4 6 100000
dis 结果
A B C D E F G
A 100000 5 7 100000 100000 100000 2
B 5 100000 100000 9 100000 100000 3
C 7 100000 100000 100000 8 100000 100000
D 100000 9 100000 100000 100000 4 100000
E 100000 100000 8 100000 100000 5 4
F 100000 100000 100000 4 5 100000 6
G 2 3 100000 100000 4 6 100000
pre 结果
A B C D E F G
A 0 0 0 0 0 0 0
B 1 1 1 1 1 1 1
C 2 2 2 2 2 2 2
D 3 3 3 3 3 3 3
E 4 4 4 4 4 4 4
F 5 5 5 5 5 5 5
G 6 6 6 6 6 6 6
最终结果格式化显示:
A 到其他顶点的最短距离
A → A = 100000 A → B = 5 A → C = 7 A → D = 100000 A → E = 100000 A → F = 100000 A → G = 2
B 到其他顶点的最短距离
B → A = 5 B → B = 100000 B → C = 100000 B → D = 9 B → E = 100000 B → F = 100000 B → G = 3
C 到其他顶点的最短距离
C → A = 7 C → B = 100000 C → C = 100000 C → D = 100000 C → E = 8 C → F = 100000 C → G = 100000
D 到其他顶点的最短距离
D → A = 100000 D → B = 9 D → C = 100000 D → D = 100000 D → E = 100000 D → F = 4 D → G = 100000
E 到其他顶点的最短距离
E → A = 100000 E → B = 100000 E → C = 8 E → D = 100000 E → E = 100000 E → F = 5 E → G = 4
F 到其他顶点的最短距离
F → A = 100000 F → B = 100000 F → C = 100000 F → D = 4 F → E = 5 F → F = 100000 F → G = 6
G 到其他顶点的最短距离
G → A = 2 G → B = 3 G → C = 100000 G → D = 100000 G → E = 4 G → F = 6 G → G = 100000
可以看到如上的输出,能方便我们查看状态图。
弗洛伊德算法核心代码
就是三层循环处理
public void floyd(MGraph mGraph) {
vertexs = mGraph.datas;
dis = mGraph.weights;
pre = new int[mGraph.vertex][mGraph.vertex];
// 初始化 pre
for (int i = 0; i < pre.length; i++) {
Arrays.fill(pre[i], i);
}
// 从中间顶点的遍历
for (int i = 0; i < vertexs.length; i++) {
// 出发顶点
for (int j = 0; j < vertexs.length; j++) {
// 终点
for (int k = 0; k < vertexs.length; k++) {
// 中间节点连接: 从 j 到 i 到 k 的距离
int lji = dis[j][i];
int lik = dis[i][k];
int leng = lji + lik;
// 直连
int ljk = dis[j][k];
// 如果间接距离比直连短,则更新
if (leng < ljk) {
dis[j][k] = leng;
/*
最难理解的是这里:
i 是已知的中间节点,前驱的时候直接设置为 i (pre[j][k] = i;) ,结果是不对的。
比如:A-G-F-D , 中间节点是是 两个节点,那么 A 到 D 的前驱节点是 F,而不是 G
F 的前驱节点是 G
如果直接赋值 i,前驱节点就会计算错误。
理解步骤为:
1. A-G-F:距离 8
A-F : 不能直连
那么设置:A,F 的前驱节点是 G; 对应这里的代码是 j,i
2. G-F-D: 距离是 10
G-D:不能直连
那么设置:G,D 的前驱节点是 F; 对应这里的代码是 i,k
3. 那么最终 A,D 的前驱节点是是什么呢?
其实就应该是 G,D 指向的值; 对应这里的代码是 i,k
*/
pre[j][k] = pre[i][k]; // 前驱节点更新为中间节点
}
}
}
}
}
测试输出结果
A B C D E F G
A 100000 5 7 100000 100000 100000 2
B 5 100000 100000 9 100000 100000 3
C 7 100000 100000 100000 8 100000 100000
D 100000 9 100000 100000 100000 4 100000
E 100000 100000 8 100000 100000 5 4
F 100000 100000 100000 4 5 100000 6
G 2 3 100000 100000 4 6 100000
dis 结果
A B C D E F G
A 4 5 7 12 6 8 2
B 5 6 12 9 7 9 3
C 7 12 14 17 8 13 9
D 12 9 17 8 9 4 10
E 6 7 8 9 8 5 4
F 8 9 13 4 5 8 6
G 2 3 9 10 4 6 4
pre 结果
A B C D E F G
A 6 0 0 6 6 6 0
B 1 6 0 1 6 6 1
C 2 0 0 5 2 4 0
D 6 3 5 5 5 3 5
E 6 6 4 5 6 4 4
F 6 6 4 5 5 3 5
G 6 6 0 5 6 6 0
最终结果格式化显示:
A 到其他顶点的最短距离
A → A = 4 A → B = 5 A → C = 7 A → D = 12 A → E = 6 A → F = 8 A → G = 2
B 到其他顶点的最短距离
B → A = 5 B → B = 6 B → C = 12 B → D = 9 B → E = 7 B → F = 9 B → G = 3
C 到其他顶点的最短距离
C → A = 7 C → B = 12 C → C = 14 C → D = 17 C → E = 8 C → F = 13 C → G = 9
D 到其他顶点的最短距离
D → A = 12 D → B = 9 D → C = 17 D → D = 8 D → E = 9 D → F = 4 D → G = 10
E 到其他顶点的最短距离
E → A = 6 E → B = 7 E → C = 8 E → D = 9 E → E = 8 E → F = 5 E → G = 4
F 到其他顶点的最短距离
F → A = 8 F → B = 9 F → C = 13 F → D = 4 F → E = 5 F → F = 8 F → G = 6
G 到其他顶点的最短距离
G → A = 2 G → B = 3 G → C = 9 G → D = 10 G → E = 4 G → F = 6 G → G = 4
关于前驱节点的计算
核心代码中有下面这样一段注释
i 是已知的中间节点,前驱的时候直接设置为 i (pre[j][k] = i;) ,结果是不对的。
比如:A-G-F-D , 中间节点是是 两个节点,那么 A 到 D 的前驱节点是 F,而不是 G
如果直接赋值 i,前驱节点就会计算错误。
理解步骤为:
1. A-G-F:距离 8
A-F : 不能直连
那么设置:A,F 的前驱节点是 G; 对应这里的代码是 j,i
2. G-F-D: 距离是 10
G-D:不能直连
那么设置:G,D 的前驱节点是 F; 对应这里的代码是 i,k
3. 那么最终 A,D 的前驱节点是是什么呢?
其实就应该是 G,D 指向的值; 对应这里的代码是 i,k
对于上面的描述,下面用图例解释下
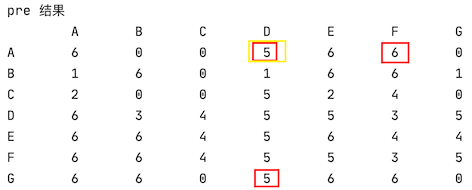
-
A-G-F,设置 A 到达 F 的前驱是 G,
A,F = 6,上图中的下标 6 就是 G这个是正确的
-
G-F-D,设置 G 到达 D 的前驱是 F,
G,D = 5,上图中的下标 5 就是 F -
那么 A-G-F-D,设置 A 到达 D 的前驱是 ?
这里需要这样来看
A - G-F-D A - X 把 A-G-F-D 看成 A-X 而 X=G-F-D G-F-D, 的前驱节点是 F 则 A-X 的前驱节点是 F 则 A-D 的前驱节点是 F


