最大熵推导LR

http://www.win-vector.com/dfiles/LogisticRegressionMaxEnt.pdf

https://www.zhihu.com/question/24094554

$\pi(x(i))_v$ 表示模型输出的样本$x_i$属于类别$v$的概率

对于多类分类：

  表示将样本$x$预测为类$v$的概率

求导：

训练集的似然函数：

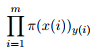
对数似然函数：

极大似然估计，对$\lambda_{u,j}$求导：

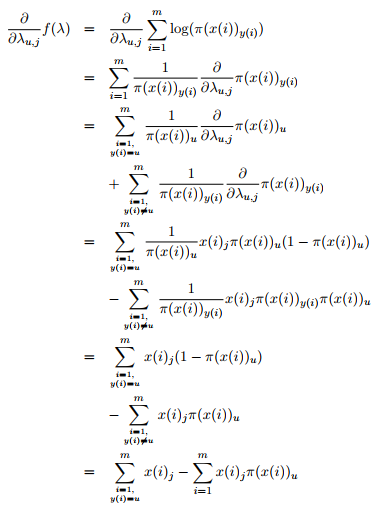
令偏导数为0，得：

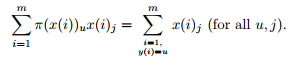
记：

 

---------------- >

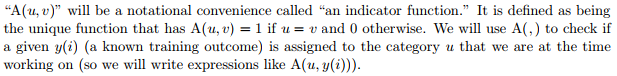
 由左式可以求出$\lambda_{u, j}$

 

---

 

由最大熵模型推导LR： LR直接使用了sigmoid函数，最大熵由任意预测函数出发，可推出LR使用sigmoid函数

求解预测函数$\pi(x)$, 可能是任意形式的函数，需满足以下三个条件：

The first two conditions are needed for $\pi ()$ to behave like a probability and the third we can think of as saying $\pi(x_i)_u$ should well approximate the category indicator     $A(u, y(i))$ on our training data.

特征函数个数应该等于类别数目，特征函数相当于对输入x(对应y(i))和输出y（对应u）同时抽取特征

由最大熵理论，求解满足以上三个条件的熵最大的模型（有约束的最优化问题）。

熵的定义：

拉格朗日函数：

 此处是不是少了一个约束条件？

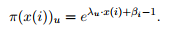
It might seem that guessing the sigmoid form is less trouble than appealing to maximum entropy. However the sigmoid is special trick (either it is appropriate or it is not) and the maximum entropy principle (and also taking partial derivatives of the Lagrangian) is a general technique.

 

http://blog.csdn.net/buring_/article/details/43342341