不均匀正负样本分布下的机器学习

 

工业界机器学习典型问题:

正负样本分布极不均匀(通常<1:10000），有什么较好的方案构造训练集的正负样本分布？构造后如何解决训练数据与预测的分布不一致？

 

  1. 上采样、下采样、代价敏感，没什么好办法。
  2. 这个之前调研过，主要分重采样和欠采样！这种不平衡是因为比率的不平衡给一些学习方法带来问题。但是在某些领域，比如反欺诈和安全，不仅是比率极不平衡，而且是正样本样本绝对数很小。需要扩散正样本方法！
  3. Synthetic Minority Over-sampling Technique 我试过这个方法，解决部分问题，主要还是需要增加样本在特征空间的覆盖！ 工程上光靠算法也解决不了问题，有的还是需要加入下经验知识来做。
  4. 用排序思想构造所谓的序对。
  5. 如果1：1０算是均匀的话，可以将多数类分割成为1000份。然后将每一份跟少数类的样本组合进行训练得到分类器。而后将这1000个分类器用assemble的方法组合位一个分类器。记得读到的论文可行，但没有验证过。
  6. 标准解决方法：设计objective function的时候给不同misclassification的情况不同的relative weights。也就是说给从小数量的样本被分成大数量的样本更大的penalty。
  7. 训练数据与预测数据分布不一致，有专门研究的课题，sample selection bias，主要方法是各种reweighting。
  8. 这个倒是可以参考positive only learning等半监督学习中如早期的spy算法等来构造合适的负例来解决正负例不平衡的问题。
  9. 这个看起来像 one-class recommendation 问题，不知是否可以考虑转化成 learning to rank 问题，如果不是为了拟合一个分布的话。
  10. 这在机器学习里面被称类别不平衡问题，可以参考Haibo, H. and E. A. Garcia (2009). “Learning from Imbalanced Data.” Knowledge and Data Engineering, IEEE Transactions on” 的survey.已有很多方法提出。
  11. 个人觉得在类别不平衡条件下，Transductive SVM (TSVM)应该对于的active learning 来标注，可能结果更好。
  12. learning to rank对于训练数据量的要求较高，同时要确定用于learning to rank的pair，还是需要找到负例，从而将正例和负例形成偏序配对。所以learning to rank是一种方法，但个人认为这会将简单问题复杂化，且本质还是需要去找负例。

 

处理内在不均衡

内在不均衡就是指数据本身特性决定了它的不均衡性。即使获取更多的数据，仍然改变不了数据的不均衡属性。

解决方案：

  1. 基本的方法是必须采用合理的性能评价指标，比如采用F1 Scorce，避免大样本类淹没了小样本类。对小样本类别的分类性能也能进行有效的评估，对数损失作为评价标准不需要对不均衡样本进行处理。
  2. 异常检测也是处理这类不均衡样本的方法，只对大样本类别进行建模，小样本类当作异常数据进行检测。
  3. 对不同类别赋予不同重要程度的权值，小样本赋予更大的权值。

F1 Score是基于准确率和召回率的单数值评估指标，数值越高效果越好

 

处理外在不均衡

外在不均衡就是指数据本身特性并不能表明它是不均衡的，是由于数据获取手段导致数据不均衡。只要获取的数据足够多，这种不均衡就能消除。

解决方案：

  1. 人工合成（伪造）数据:前提是了解数据，拥有足够的先验知识
  2. 采集更多的数据。

注意：

通过重采样将数据变得均衡不一定能提升分类性能，比如不能提升logistic回归性能，但对随机森林有效（但随机森林不适合用于不均衡数据）

参考： http://www.win-vector.com/blog/2015/02/does-balancing-classes-improve-classifier-performance/ 需要再看

转自：

http://qianjiye.de/2014/12/unbalanced-data-sets#lin_ml_ne_2014    

 

 

https://zhuanlan.zhihu.com/p/21406238

在类别不平衡的情况下，对模型使用F值或者AUC值是更好的选择。

处理不平衡数据，可以从两方面考虑：一是改变数据分布，从数据层面使得类别更为平衡；

二是改变分类算法，在传统分类算法的基础上对不同类别采取不同的加权方式，使得模型更看重少数类。

本部分对数据层面的一些方法做一个介绍，改变数据分布的方法主要是重采样：

  • 欠采样：减少多数类样本的数量

  • 过采样：增加少数类样本的数量

  • 综合采样：将过采样和欠采样结合

一、欠采样

随机欠采样

减少多数类样本数量最简单的方法便是随机剔除多数类样本，可以事先设置多数类与少数类最终的数量比例ratio，在保留少数类样本不变的情况下，根据ratio随机选择多数类样本。

  • 优点：操作简单，只依赖于样本分布，不依赖于任何距离信息，属于非启发式方法。

  • 缺点：会丢失一部分多数类样本的信息，无法充分利用已有信息。

Tomek links方法

首先来看一些定义。

假设样本点xi和xj属于不同的类别，d(xi,xj)表示两个样本点之间的距离。

称(xi,xj)为一个Tomek link对，如果不存在第三个样本点xl使得d(xl,xi)<d(xi,xj)或者d(xl,xj)<d(xi,xj)成立。

容易看出，如果两个样本点为Tomek link对，则其中某个样本为噪声（偏离正常分布太多）或者两个样本都在两类的边界上。

Tomek link对一般有两种用途：

  • 欠采样：将Tomek link对中属于多数类的样本剔除。

  • 数据清洗：将Tomek link对中的两个样本都剔除。

NearMiss方法

NearMiss方法是利用距离远近剔除多数类样本的一类方法，实际操作中也是借助kNN，总结起来有以下几类：

  • NearMiss-1：在多数类样本中选择与最近的3个少数类样本的平均距离最小的样本。

  • NearMiss-2：在多数类样本中选择与最远的3个少数类样本的平均距离最小的样本。

  • NearMiss-3：对于每个少数类样本，选择离它最近的给定数量的多数类样本。

NearMiss-1和NearMiss-2方法的描述仅有一字之差，但其含义是完全不同的：NearMiss-1考虑的是与最近的3个少数类样本的平均距离，是局部的；NearMiss-2考虑的是与最远的3个少数类样本的平均距离，是全局的。

NearMiss-1方法得到的多数类样本分布也是“不均衡”的，它倾向于在比较集中的少数类附近找到更多的多数类样本，而在孤立的（或者说是离群的）少数类附近找到更少的多数类样本，原因是NearMiss-1方法考虑的局部性质和平均距离。

NearMiss-3方法则会使得每一个少数类样本附近都有足够多的多数类样本，显然这会使得模型的精确度高、召回率低。

论文中有对这几种方法的比较，得到的结论是NearMiss-2的效果最好，不过这也是需要综合考虑数据集和采样比例的不同造成的影响。

二、过采样

随机过采样

与欠采样对应，增加少数类样本数量最简单的方法便是随机复制少数类样本，可以事先设置多数类与少数类最终的数量比例ratio，在保留多数类样本不变的情况下，根据ratio随机复制少数类样本。

在使用的过程中为了保证所有的少数类样本信息都会被包含，可以先完全复制一份全量的少数类样本，再随机复制少数类样本使得数量比例满足给定的ratio。

  • 优点：操作简单，只依赖于样本分布，不依赖于任何距离信息，属于非启发式方法。

  • 缺点：重复样本过多，容易造成分类器的过拟合。

SMOTE （算法实现：http://blog.csdn.net/march_on/article/details/48650237）

SMOTE全称为Synthetic Minority Over-sampling Technique，主要思想来源于手写字识别：对于手写字的图片而言，旋转、扭曲等操作是不会改变原始类别的（要排除翻转和180度大规模旋转这类的操作，因为会使得“9”和“6”的类别发生变化），因而可以产生更多的样本。

SMOTE的主要思想也是通过在一些位置相近的少数类样本中生成新样本达到平衡类别的目的，由于不是简单地复制少数类样本，因此可以在一定程度上避免分类器的过度拟合。

其算法流程如下：

  1. 设置向上采样的倍率为N，即对每个少数类样本都需要产生对应的N个少数类新样本。

  2. 对少数类中的每一个样本x，搜索得到其k（通常取5）个少数类最近邻样本，并从中随机选择N个样本，记为y1,y2,…,yN（可能有重复值）。

  3. 构造新的少数类样本rj=x+rand(0,1)∗(yj−x)，其中rand(0,1)表示区间(0,1)内的随机数。（对每个少数类样本a，从它的最近邻中随机选一个样本b，然后在a、b之间的连线上随机选一点作为新合成的少数类样本）

三、综合采样

目前为止我们使用的重采样方法几乎都是只针对某一类样本：对多数类样本欠采样，对少数类样本过采样。也有人提出将欠采样和过采样综合的方法，解决样本类别分布不平衡和过拟合问题，本部分介绍其中的两个例子：SMOTE+Tomek links和SMOTE+ENN。

SMOTE+Tomek links

SMOTE+Tomek links方法的算法流程非常简单：

  1. 利用SMOTE方法生成新的少数类样本，得到扩充后的数据集T

  2. 剔除T中的Tomek links对。

普通SMOTE方法生成的少数类样本是通过线性差值得到的，在平衡类别分布的同时也扩张了少数类的样本空间，产生的问题是可能原本属于多数类样本的空间被少数类“入侵”（invade），容易造成模型的过拟合。

Tomek links对寻找的是那种噪声点或者边界点，可以很好地解决“入侵”的问题。

SMOTE+ENN

SMOTE+ENN方法和SMOTE+Tomek links方法的想法和过程都是很类似的：

  1. 利用SMOTE方法生成新的少数类样本，得到扩充后的数据集T。

  2. 对T中的每一个样本使用kNN（一般k取3）方法预测，若预测结果和实际类别标签不符，则剔除该样本。

四、Informed Understanding

SMOTE算法是为了解决随机过采样容易发生的模型过拟合问题，对应的也有一些方法解决随机欠采样造成的数据信息丢失问题。本部分的Informed Undersampling是对欠采样的补充，因为其中有一些集成（ensemble）的想法，因此单独介绍。

EasyEnsemble

EasyEnsemble的想法非常简单，假设少数类样本集合为P，多数类样本集合为N，样本量分别为|P|和|N|，其算法流程如下：

随机欠采样会导致信息缺失，EasyEnsemble的想法则是多次随机欠采样，尽可能全面地涵盖所有信息，算法特点则是利用boosting减小偏差（AdaBoost）、bagging减小方差（集成分类器）。实际应用的时候也可以尝试选用不同的分类器来提高分类的效果。

BalanceCascade

EasyEnsemble算法训练的子过程是独立的，BalanceCascade则一种级联算法，这种级联的思想在图像识别中用途非常广。论文中详细描述了BalanceCascade的算法流程：

BalanceCascade算法得到的是一个级联分类器，将若干个强分类器由简单到复杂排列，只有和少数类样本特征比较接近的才有可能输入到后面的分类器，比如边界点，因此能更充分地利用多数类样本的信息，一定程度上解决随机欠采样的信息丢失问题。

 

改变分类算法

代价矩阵

采样算法从数据层面解决不平衡数据的学习问题，在算法层面上解决不平衡数据学习的方法主要是基于代价敏感学习算法(Cost-Sensitive Learning)，代价敏感学习方法的核心要素是代价矩阵，我们注意到在实际的应用中不同类型的误分类情况导致的代价是不一样的，例如在医疗中，“将病人误疹为健康人”和“将健康人误疹为病人”的代价不同；在信用卡盗用检测中，“将盗用误认为正常使用”与“将正常使用识破认为盗用”的代价也不相同，因此我们定义代价矩阵如下图5所示。标记Cij为将类别j误分类为类别i的代价，显然C_00=C_11=0，C_01,C_10为两种不同的误分类代价，当两者相等时为代价不敏感的学习问题。

 

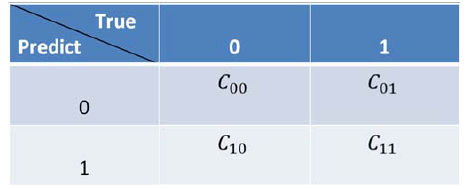
基于以上代价矩阵的分析，代价敏感学习方法主要有以下三种实现方式，分别是：

1、从学习模型出发，着眼于对某一具体学习方法的改造，使之能适应不平衡数据下的学习，研究者们针对不同的学习模型如感知机，支持向量机，决策树，神经网络等分别提出了其代价敏感的版本。以代价敏感的决策树为例，可从三个方面对其进行改进以适应不平衡数据的学习，这三个方面分别是决策阈值的选择方面、分裂标准的选择方面、剪枝方面，这三个方面中都可以将代价矩阵引入，具体实现算法可参考参考文献中的相关文章。
2、从贝叶斯风险理论出发，把代价敏感学习看成是分类结果的一种后处理（先验信息），按照传统方法学习到一个模型，以实现损失最小为目标对结果进行调整，优化公式如下所示。此方法的优点在于它可以不依赖所用具体的分类器，但是缺点也很明显它要求分类器输出值为概率。

 

3、从预处理的角度出发，将代价用于权重的调整，使得分类器满足代价敏感的特性，下面讲解一种基于Adaboost的权重更新策略。

 

AdaCost算法修改了Adaboost算法的权重更新策略，其基本思想是对于代价高的误分类样本大大地提高其权重，而对于代价高的正确分类样本适当地降低其权重，使其权重降低相对较小。总体思想是代价高样本权重增加得大降低得慢。其样本权重按照如下公式进行更新。其中$\beta_+$和  \beta_{-} 分别表示样本被正确和错误分类情况下 $ \beta $ 的取值。

 

 

  

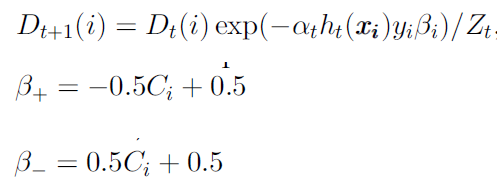
参考：

 
http://www.jianshu.com/p/3e8b9f2764c8


posted @ 2017-03-01 17:04  合唱团abc  阅读(14809)  评论(0)  编辑  收藏  举报