FTRL (Follow-the-regularized-Leader)算法
Online gradient descent(OGD) produces excellent prediction accuracy with a minimum of computing resources.However, in practice another key consideration is the size of the final model;Since models can be stored sparsely, the number of non-zero coefficients in W is the determining factor of memory usage.
Without regularization , FTRL-Proximal is identical to standard online gradient descent, but because it uses an alternative lazy representation of the model coefficients w, L1 regularization can be implemented much more effectively.
Given a sequence of gradients $g_t$, OGD performs the update $W_{t+1} = W_t - \eta_tg_t$ , where $\eta_t$ is a non-increasing learning-rate schedule,e.g.$\eta_t = 1 / \sqrt{t}$.
The FTRL-Proximal algorithm uses the update $W_{t+1} = arg_wmin(g_{1:t}.w + 1/2 \sum_{s=1}^t\sigma_s ||w - w_s||_2^2 + \lambda_1||w||_1)$, $\sigma_{1:t} = 1 / \eta_t$
when we take $\lambda_1 = 0$, they produce an identical sequence of coefficient vectors. However, the FTRL-Proximal update with $\lambda_1 > 0$ does an excellent job of inducing sparsity.

其中,
式中第一项是对损失函数的贡献的一个估计,第二项是控制w(也就是model)在每次迭代中变化不要太大,第三项代表L1正则(获得稀疏解),表示学习速率。
学习速率可以通过超参数自适应学习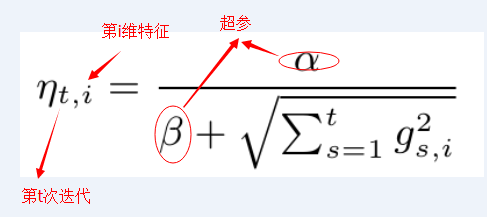
we can re-write the update as the argmin over w of
$(g_{1:t} - \sum_{s=1}^t\sigma_sw_s) . w + (1 / \eta_t) ||w||^2_2 + \lambda_1||w||_1 + const$ (左式第二项少了个1/2)
Let $z_{t-1} = g_{1:t-1} - \sum_{s=1}^{t-1}\sigma_sw_s$, so $z_t = z_{t-1} + g_t - (1/\eta_t - 1/ (\eta_{t-1}))W_t$ and solve for $W_{t+1}$ in closed form on a percoordinate bases by

Note that when $\eta_t$ is a constant value $\eta$ and $\lambda_1 = 0$, it is easy to see the equivalence to online gradient descent, since we have $W_{t+1} = -\etaZ_t =-\eta \sum^t_{s=1}g_s$

FTRL综合考虑了FOBOS和RDA对于正则项和W限制的区别,其特征权重的更新公式为:
注意,公式(3)中出现了L2正则项,在论文[2]的公式中并没有这一项,但是在其2013年发表的FTRL工程化实现的论文[3]却使用到了L2正则项。事实上该项的引入并不影响FRTL的稀疏性,后面的推导过程会显示这一点。L2正则项的引入仅仅相当于对最优化过程多了一个约束,使得结果求解结果更加“平滑”。
公式(3)看上去很复杂,更新特征权重貌似非常困难的样子。不妨将其进行改写,将最后一项展开,等价于求下面这样一个最优化问题:
上式中最后一项相对于来说是一个常数项,并且令
,上式等价于:
针对特征权重的各个维度将其拆解成N个独立的标量最小化问题:
到这里,我们遇到了与上一篇RDA中类似的优化问题,用相同的分析方法可以得到:
从公式(4)可以看出,引入L2正则化并没有对FTRL结果的稀疏性产生任何影响。公式4可以用软阈值分析求解,但是怎么和$sgn(z_i^{(t)})$联系起来?
前面介绍了FTRL的基本推导,但是这里还有一个问题是一直没有被讨论到的:关于学习率的选择和计算。事实上在FTRL中,每个维度上的学习率都是单独考虑的(Per-Coordinate Learning Rates)。
在一个标准的OGD里面使用的是一个全局的学习率策略,这个策略保证了学习率是一个正的非增长序列,对于每一个特征维度都是一样的。
考虑特征维度的变化率:如果特征1比特征2的变化更快,那么在维度1上的学习率应该下降得更快。我们很容易就可以想到可以用某个维度上梯度分量来反映这种变化率。在FTRL中,维度i上的学习率是这样计算的:
由于,所以公式(4)中有
,这里的
和
是需要输入的参数,公式(4)中学习率写成累加的形式,是为了方便理解后面FTRL的迭代计算逻辑。
参考:
http://blog.csdn.net/wenzishou/article/details/73558017
RDA优化: http://www.cnblogs.com/luctw/p/4757943.html
http://blog.csdn.net/a819825294/article/details/51227265




