ffm算法
www.csie.ntu.edu.tw/~cjlin/papers/ffm.pdf 读书笔记
The effect of feature conjunctions(组合特征) is difficult for linear models(比如LR) to learn because they learn the two weights separately(学习LR模型时，不同的参数是独立学习的).
用于组合特征的两个模型：
1. degree-2 polynomial mappings(Poly2) 二阶多项式
2. FM(factorization machines)算法 ,在上个模型的基础上使用矩阵分解，原模型的每个二次项参数Wi,j都对应两个latent vectors的点积。(Wi,j = <Vi,Vj>, W =VVT ,V的行向量是latent vector, VT的列向量是latent vector,其实就是$V_i,V_j$是$X_i,X_j$隐向量)
二阶多项式模型：
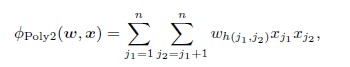
$h(_{j1},_{j2})$ is a function encoding $j_1$ and $j_2$ into a natural number.The naive way to implement $h(_{j1},_{j2})$ is to consider every pair of features as a new feature .This approach requires the model as large as O(n^2),which is ususlly impractical for CTR prediction because of very large n.We can solve this problem by hashing $j_1$ and $j_2$.(肯定有很多组合特征$x_ix_j$的系数$w_{ij}$为0，如果采用上述naive的方式，浪费了很多内存)(参照vowpal wabbit)
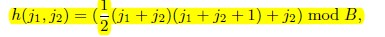the model size B is a user-specified parameter.
FM算法中，每一个特征 $X_i$ 对应一个隐变量 $V_i$。(In FMs,every feature has only one latent vector to learn the latent effect with any other features)
field指的是one-hot encoding前的特征，FM算法先做one-hot encoding,然后对编码后的每个特征使用一个latent vector（这里应该错误的）,而在FFM算法中，每个特征有多个latent vectors,个数应该是field数-1,组合特征系数等于field下的latent vector的点积.
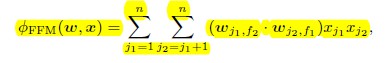
在FFM算法中，每个field对应一个latent vector,这样一来，该latent vector的元素个数k远小于FM算法中隐向量的维度k.
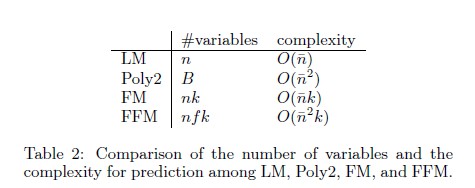
简单来说，同一个categorical特征经过One-Hot编码生成的数值特征都可以放到同一个field，包括用户性别、职业、品类偏好等。在FFM中，每一维特征$x_i$,针对其它特征的每一种field $f_j$, 都会学习一个隐向量 $v_{i,f_j}$,因此，隐向量不仅与特征相关，也与field相关,隐向量的数目为one-hot后的特征数 * field数。
假设样本的$n$个特征属于$f$个field，那么FFM的二次项有$nf$个隐向量。而在FM模型中，每一维特征的隐向量只有一个。FM可以看作FFM的特例，是把所有特征都归属到一个field时的FFM模型。
为了使用FFM方法，所有的特征必须转换成“field_id:feat_id:value”格式，field_id代表特征所属field的编号，feat_id是特征编号，value是特征的值。数值型的特征比较容易处理，只需分配单独的field编号，如用户评论得分、商品的历史CTR/CVR等。categorical特征需要经过One-Hot编码成数值型，编码产生的所有特征同属于一个field，而特征的值只能是0或1，如用户的性别、年龄段，商品的品类id等。除此之外，还有第三类特征，如用户浏览/购买品类，有多个品类id且用一个数值衡量用户浏览或购买每个品类商品的数量。这类特征按照categorical特征处理，不同的只是特征的值不是0或1，而是代表用户浏览或购买数量的数值。按前述方法得到field_id之后，再对转换后特征顺序编号，得到feat_id，特征的值也可以按照之前的方法获得。关键在于feat_id如何表示？（hash）
参考：
http://tech.meituan.com/deep-understanding-of-ffm-principles-and-practices.html
