核函数以及SVM相关知识（重点）

http://www.cnblogs.com/jerrylead/archive/2011/03/18/1988406.html

http://blog.pluskid.org/?p=685

考虑我们最初在“线性回归”中提出的问题，特征是房子的面积x，这里的x是实数，结果y是房子的价格。假设我们从样本点的分布中看到x和y符合3次曲线，那么我们希望使用x的三次多项式来逼近这些样本点。那么首先需要将特征x扩展到三维，然后寻找特征和结果之间的模型。我们将这种特征变换称作特征映射（feature mapping）。映射函数称作，在这个例子中

我们希望将得到的特征映射后的特征应用于SVM分类，而不是最初的特征。这样，我们需要将前面公式中的内积从，映射到。

至于为什么需要映射后的特征而不是最初的特征来参与计算，上面提到的（为了更好地拟合）是其中一个原因，另外的一个重要原因是样例可能存在线性不可分的情况，而将特征映射到高维空间后，往往就可分了。（在《数据挖掘导论》Pang-Ning Tan等人著的《支持向量机》那一章有个很好的例子说明）

将核函数形式化定义，如果原始特征内积是，映射后为，那么定义核函数（Kernel）为

到这里，我们可以得出结论，如果要实现该节开头的效果，只需先计算，然后计算即可，然而这种计算方式是非常低效的。比如最初的特征是n维的，我们将其映射到维，然后再计算，这样需要的时间。那么我们能不能想办法减少计算时间呢？

先看一个例子，假设x和z都是n维的，

展开后，得

这个时候发现我们可以只计算原始特征x和z内积的平方（时间复杂度是O(n)），就等价与计算映射后特征的内积。也就是说我们不需要花时间了。

我的理解：有些问题，原始数据是线性不可分的，映射到高维空间是可分的。这时可能需要计算映射到高维空间后的两个向量($n^2$维度)的点积，如果先映射到高维空间再计算点积，复杂度是$O(n^2)$, 但是先计算低维空间的两个向量(维度是$n$)的点积，然后通过核函数映射到高维空间，复杂度是$O(n)$

核技巧是通过一个非线性变换将输入空间对应于一个特征空间，使得在输入空间中的超曲面模型对应于特征空间中的超平面模型。对于给定的核函数$k(x,y)$, 特征空间和映射函数的取法并不唯一，可以取不同的特征空间，即便是同一特征空间里也可以取不同的映射。在实际应用中，往往依赖领域知识直接选择核函数，核函数选择的有效性需要通过实验验证。

 

 

---

1.线性内核
使用线性内核，其实就等价于没有内核，特征映射的过程是简单的线性变换。公式如下所示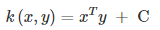：这实际上就是原始空间中的内积,这个核存在的主要目的是使得“映射后空间中的问题”和“映射前空间中的问题”两者在形式上统一起来了。

2.多项式内核

该空间的维度是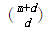,其中m是原始空间的维度

3.高斯（RBF）内核

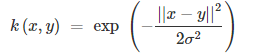
这个核会将原始空间映射为无穷维空间。不过，如果$\sigma$选得很大的话，高次特征上的权重实际上衰减的非常快，所以实际上（数值上近似一下）相当于一个低维的子空间；反过来，如果$\sigma$选的很小，则可以将任意的数据映射为线性可分，不过这并不一定是好事，因为随之而来的可能是非常严重的过拟合问题。不过，总的来说，通过调控参数$\sigma$高斯核实际上具有相当高的灵活性，也是使用最广泛的核函数之一。

两向量：$x = (x_1, x_2)$, $y = (y_1, y_2)$

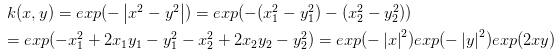 左式有点错误，第三步少了平方，注意下

根据泰勒公式，

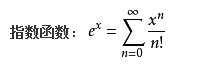
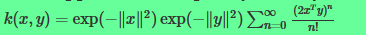
可以看出公式中的的泰勒展开式其实是0-n维的多项式核函数的和。

 

---

svm 为啥要用拉格朗日对偶算法来解最大化（几何）间隔问题：

并不一定要用拉格朗日对偶。要注意用拉格朗日对偶并没有改变最优解，而是改变了算法复杂度：在原问题下，求解算法的复杂度与样本维度（等于权值w的维度）有关；而在对偶问题下，求解算法的复杂度与样本数量（等于拉格朗日算子a的数量，即支持向量数目）有关。

因此，如果你是做线性分类，且样本维度低于样本数量的话，在原问题下求解就好了，Liblinear之类的线性SVM默认都是这样做的；但如果你是做非线性分类，那就会涉及到升维（比如使用高斯核做核函数，其实是将样本升到无穷维），升维后的样本维度往往会远大于样本数量，此时显然在对偶问题下求解会更好（线性内核一般在原问题下求解，高斯内核在对偶问题下求解）。

 

SVM优缺点： http://blog.sina.com.cn/s/blog_6d979ba00100oel2.html

SVM有如下主要几个特点： 
(1)非线性映射是SVM方法的理论基础,SVM利用内积核函数代替向高维空间的非线性映射； 
(2)对特征空间划分的最优超平面是SVM的目标,最大化几何间隔的思想是SVM方法的核心； 
(3)支持向量是SVM的训练结果,在SVM分类决策中起决定作用的是支持向量；
(4)SVM 是一种有坚实理论基础的新颖的小样本学习方法。
它基本上不涉及概率测度及大数定律等,因此不同于现有的统计方法。
从本质上看,它避开了从归纳到演绎的传统过程,实现了高效的从训练样本到预报样本的“转导推理”,
大大简化了通常的分类和回归等问题； 
(5)SVM 的最终决策函数只由少数的支持向量所确定,计算的复杂性取决于支持向量的数目,
而不是样本空间的维数,这在某种意义上避免了“维数灾难”。 
(6)少数支持向量决定了最终结果,这不但可以帮助我们抓住关键样本、“剔除”大量冗余样本,
而且注定了该方法不但算法简单,而且具有较好的“鲁棒”性。

这种“鲁棒”性主要体现在: 
①增、删非支持向量样本对模型没有影响; 
②支持向量样本集具有一定的鲁棒性; 
③有些成功的应用中,SVM 方法对核的选取不敏感 

两个不足： 
(1) SVM算法对大规模训练样本难以实施 由于SVM是借助二次规划来求解支持向量，
而求解二次规划将涉及m阶矩阵的计算（m为样本的个数），当m数目很大时该矩阵的存储和计算
将耗费大量的机器内存和运算时间。
针对以上问题的主要改进有
J.Platt的SMO算法、
T.Joachims的SVM、
C.J.C.Burges等的PCGC、
张学工的CSVM
以及O.L.Mangasarian等的SOR算法 

(2) 用SVM解决多分类问题存在困难 
经典的支持向量机算法只给出了二类分类的算法，
而在数据挖掘的实际应用中，一般要解决多类的分类问题。
可以通过多个二类支持向量机的组合来解决。
主要有
一对多组合模式、一对一组合模式和SVM决策树；
再就是通过构造多个分类器的组合来解决。
主要原理是克服SVM固有的缺点，结合其他算法的优势，解决多类问题的分类精度。

 

SVM高斯核调参：http://www.cnblogs.com/pinard/p/6126077.html

SVM分类模型两个超参数是惩罚系数C和RBF核函数的系数$\gamma$。惩罚系数C即松弛变量的系数。它在优化函数里主要是平衡支持向量的复杂度和误分类率这两者之间的关系，可以理解为正则化系数。当C比较大时，我们的损失函数也会越大，这意味着我们不愿意放弃比较远的离群点。这样我们会有更加多的支持向量，也就是说支持向量和超平面的模型也会变得越复杂，也容易过拟合（C大，表示松弛变量项的权重较大，算法尽量拟合那些离群点，导致过拟合）。反之，当C比较小时，意味我们不想理那些离群点，会选择较少的样本来做支持向量，最终的支持向量和超平面的模型也会简单。scikit-learn中默认值是1。

另一个超参数是RBF核函数的参数$\gamma$，RBF核函数$K(x, z) = exp(-\gamma ||x - z||^2), \gamma > 0$，$\gamma$主要定义了单个样本对整个分类超平面的影响，当$\gamma$比较小时，高次特征上的权重实际上衰减的非常快，单个样本对整个分类超平面的影响比较小，不容易被选择为支持向量，反之，当$\gamma$比较大时，可以将任意的数据映射为线性可分，单个样本对整个分类超平面的影响比较大，更容易被选择为支持向量，或者说整个模型的支持向量也会多。scikit-learn中默认值是1/ 样本特征数。

如果把惩罚系数C和RBF核函数的系数$\gamma$一起看，当C比较大，$\gamma$比较大时，我们会有更多的支持向量，我们的模型会比较复杂，容易过拟合。

SVM回归模型的RBF核比分类模型要复杂一点，因为此时我们除了惩罚系数C和RBF核函数的系数$\gamma$之外，还多了一个损失距离度量$\epsilon$。对于惩罚系数和RBF核函数的系数，回归模型和分类模型的作用基本相同。对于损失距离度量$\epsilon$,它决定了样本点到超平面的距离损失，当$\epsilon$比较大时， 损失较小，更多的点在损失距离范围之内，而没有损失,模型较简单，而当$\epsilon$比较小时，损失函数会较大，模型也会变得复杂，scikit-learn中默认值是0.1。

主要调参方法：gridsearch + 交叉验证（每个参数组合都进行k折验证吗，这样训练时间太长了吧）

　对于SVM的RBF核，我们主要的调参方法都是交叉验证。具体在scikit-learn中，主要是使用网格搜索，即GridSearchCV类。当然也可以使用cross_val_score类来调参，但是个人觉得没有GridSearchCV方便。本文我们只讨论用GridSearchCV来进行SVM的RBF核的调参。

 　　　　我们将GridSearchCV类用于SVM RBF调参时要注意的参数有：

　　　　1) estimator :即我们的模型，此处我们就是带高斯核的SVC或者SVR

　　　　2) param_grid：即我们要调参的参数列表。 比如我们用SVC分类模型的话，那么param_grid可以定义为{"C":[0.1, 1, 10], "gamma": [0.1, 0.2, 0.3]}，这样我们就会有9种超参数的组合来进行网格搜索，选择一个拟合分数最好的超平面系数。

　　　　3) cv: S折交叉验证的折数，即将训练集分成多少份来进行交叉验证。默认是3,。如果样本较多的话，可以适度增大cv的值。

　　　　网格搜索结束后，我们可以得到最好的模型estimator, param_grid中最好的参数组合，最好的模型分数。

 

核函数矩阵数值的大小有什么含义？

http://www.cnblogs.com/jerrylead/archive/2011/03/18/1988406.html 

 

 

---

 

Andrew Ng理论1：当数据量足够庞大时，feature足够多时，所有的分类算法最终的效果都差不多。也就是说，不管你选用什么样的核，在训练集够大的情况下都是然并卵。当然，就分类效果来说，非线性的比线性的核好一些。但线性的也能够有很不错的分类效果，而且计算量比非线性小，所以需要具体情况具体分析。

Andrew Ng理论2: 老实人Andrew教你如何选择合适的SVM核。
情况1：当训练集不大，feature比较多的时候，用线性的核。因为多feature的情况下就已经可以给线性的核提供不错的variance去fit训练集。

情况2：当训练集相对可观，而feature比较少，用非线性的核。因为需要算法提供更多的variance去fit训练集。

情况3：feature少，训练集非常大，用线性的核。因为非线性的核需要的计算量太大了。