梯度下降法的三种形式BGD、SGD以及MBGD
http://www.cnblogs.com/maybe2030/p/5089753.html
在应用机器学习算法时,我们通常采用梯度下降法来对采用的算法进行训练。其实,常用的梯度下降法还具体包含有三种不同的形式,它们也各自有着不同的优缺点。
下面我们以线性回归算法来对三种梯度下降法进行比较。
一般线性回归函数的预测函数为: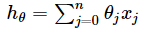
对应的损失函数形式为: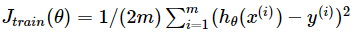
1. 批量梯度下降法BGD
批量梯度下降法(Batch Gradient Descent,简称BGD)是梯度下降法最原始的形式,它的具体思路是在更新每一参数时都使用所有的样本来进行更新,其数学形式如下:
(1) 对上述的损失函数求偏导:
(2) 由于是最小化风险函数,所以按照每个参数θ的梯度负方向来更新每个θ:
具体的伪代码形式为:
repeat{
(for every j=0, ... , n)
}
从上面公式可以注意到,它得到的是一个全局最优解,但是每迭代一步,都要用到训练集所有的数据,如果样本数目很大,那么可想而知这种方法的迭代速度!所以,这就引入了另外一种方法,随机梯度下降。
优点:全局最优解;易于并行实现;
缺点:当样本数目很多时,训练过程会很慢。
2. 随机梯度下降法SGD
由于批量梯度下降法在更新每一个参数时,都需要所有的训练样本,所以训练过程会随着样本数量的加大而变得异常的缓慢。随机梯度下降法(Stochastic Gradient Descent,简称SGD)正是为了解决批量梯度下降法这一弊端而提出的。
将上面的损失函数写为如下形式:
利用每个样本的损失函数cost对θ求偏导得到对应的梯度,来更新θ:
![]()
具体的伪代码形式为:
1. Randomly shuffle dataset;
2. repeat{
for i=1, ... , mm{
(for j=0, ... , n)
}
}
随机梯度下降是通过每个样本来迭代更新一次,如果样本量很大的情况(例如几十万),那么可能只用其中几万条或者几千条的样本,就已经将theta迭代到最优解了,对比上面的批量梯度下降,迭代一次需要用到十几万训练样本,一次迭代不可能最优,如果迭代10次的话就需要遍历训练样本10次。但是,SGD伴随的一个问题是噪音较BGD要多,使得SGD并不是每次迭代都向着整体最优化方向。(贪心算法,局部最优解)
SGD is just one type of online learning algorithm. There are many other online learning algorithms that may not depend on gradients (e.g. perceptron algorithm, bayesian inference, etc).
优点:训练速度快;
缺点:准确度下降,并不是全局最优;不易于并行实现。
3. 小批量梯度下降法MBGD
有上述的两种梯度下降法可以看出,其各自均有优缺点,那么能不能在两种方法的性能之间取得一个折衷呢?即,算法的训练过程比较快,而且也要保证最终参数训练的准确率,而这正是小批量梯度下降法(Mini-batch Gradient Descent,简称MBGD)的初衷。
MBGD在每次更新参数时使用b个样本(b一般为10),其具体的伪代码形式为:
Say b=10, m=1000.
Repeat{
for i=1, 11, 21, 31, ... , 991{

(for every j=0, ... , n)
}
}
4. 总结
Batch gradient descent: Use all examples in each iteration;
Stochastic gradient descent: Use 1 example in each iteration;
Mini-batch gradient descent: Use b examples in each iteration.
http://www.codelast.com/%E5%8E%9F%E5%88%9B-%E5%86%8D%E8%B0%88-%E6%9C%80%E9%80%9F%E4%B8%8B%E9%99%8D%E6%B3%95%E6%A2%AF%E5%BA%A6%E6%B3%95steepest-descent/ 这篇博客说明了为什么负梯度方向是下降最快方向以及梯度下降法的优缺点
http://www.cnblogs.com/EE-NovRain/p/3810737.html 可以参考下






