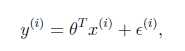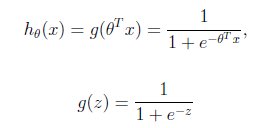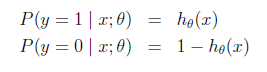对线性回归，logistic回归和一般回归的认识

http://www.cnblogs.com/llhthinker/p/5248586.html

http://www.cnblogs.com/jerrylead/archive/2011/03/05/1971867.html

Feature Scaling（数据规范化）

不同的特征量由于单位不同，可能在数值上相差较大，Feature Scaling可以去量纲，减少梯度下降法的迭代次数，提高速度，所以在算法执行前通常需要Feature Scaling。直观上来说，考虑两个特征量，规范化前的椭圆很瘪，可能导致收敛的路径变长，数据规范化后使得椭圆较均匀，缩短收敛路径，如下：

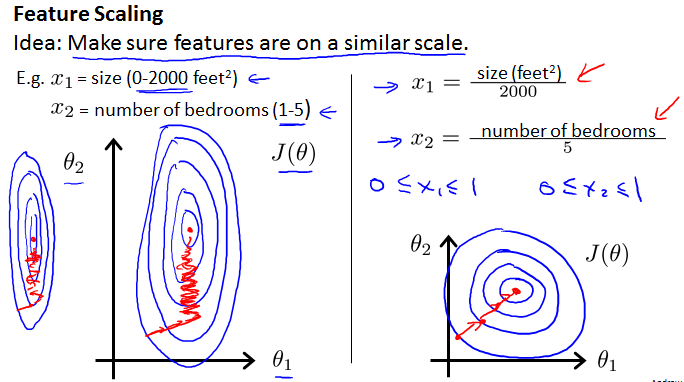
下面给出一种规范化策略:

1. 求每个特征量X的平均值mean
2. 求每个特征量X的标准差sigma         (matlab中std()函数)
3. 规范化：X = (X-mean) / sigma

Normal equation（正则方程）

Normal equation: Method to solve for analytically.

首先考虑cost function J的自变量theta为一维的情况，这时的J为关于theta的一元二次函数，可以直接求导得到最小值点，如下图所示:

 

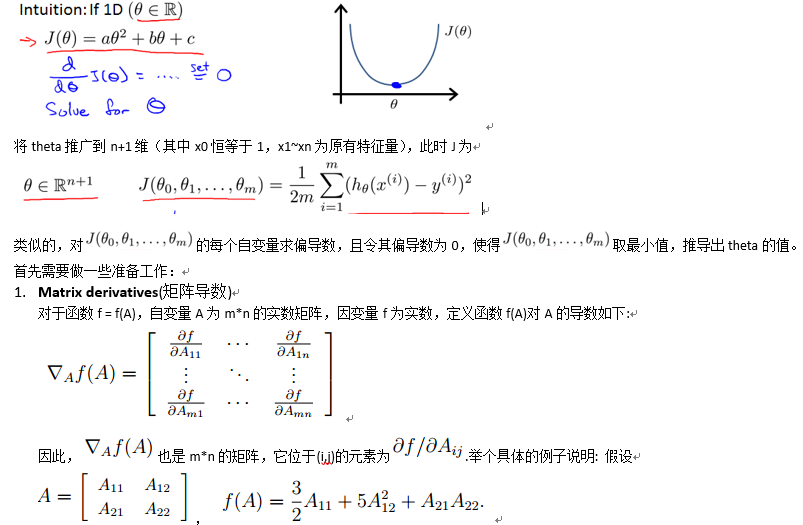
下面对Gradient Descent 和 Normal Equation做一下比较(这两种方法都可以用来求解线性回归问题)

•   m = 20000, n = 10000，优先考虑Gradient Descent
•   m = 20000, n = 10, 优先考虑Normal Equation(当特征数量大时,norm equation方法计算量很大，速度会很慢)

迭代次数和learning rate是影响梯度下降法是否成功收敛到最优值的重要因素。

• 迭代次数：
  • 过少可能使得算法还没有收敛就停止，
  • 过多导致资源（时间等）的浪费；
• learning rate:
  • 过小，使得每次迭代时theta的变化量过小，从而算法收敛过慢，换言之需要增加迭代次数使得算法收敛；
  • 过大，使得每次迭代时theta的变化量过大，可能在变化（迭代）过程中越过最优（收敛）点。

损失函数为平方误差的概率解释

假设根据特征的预测结果与实际结果有误差，那么预测结果和真实结果满足下式：

     一般来讲，误差满足平均值为0的高斯分布，也就是正态分布（此处假设符合客观规律）。那么x和y的条件概率也就是

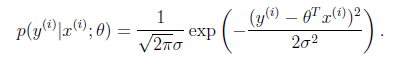由eⁱ的概率分布推导而来，eⁱ服从正态分布，而eⁱ的概率分布即yⁱ|xⁱ的概率分布

     这样就估计了一条样本的结果概率，然而我们期待的是模型能够在全部样本上预测最准，也就是概率积最大。注意这里的概率积是概率密度函数积，连续函数的概率密度函数与离散值的概率函数不同。这个概率积成为最大似然估计。我们希望在最大似然估计得到最大值时确定θ。那么需要对最大似然估计公式求导，求导结果既是

          

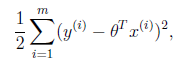
我的理解：每个样本点的真实值可表示为预测值与预测误差之和，假设预测误差服从均值为0的正态分布，则y关于x的条件概率也服从该分布，为了让模型能够在全部样本上预测最准，即求P(y|x)关于每个样本点的乘积最大时的参数，也就是最大似然估计。由极大似然估计可以推导出线性回归的损失函数

---

 

带权重的线性回归

     上面提到的线性回归的误差函数里系统都是1，没有权重。带权重的线性回归加入了权重信息。

     基本假设是

          

     其中假设符合公式

               

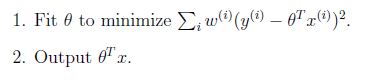
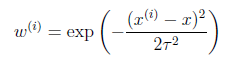
     其中x是要预测的特征，这样假设的道理是离x越近的样本权重越大，越远的影响越小。这个公式与高斯分布类似，但不一样，因为不是随机变量。

     此方法成为非参数学习算法，因为误差函数随着预测值的不同而不同，这样θ无法事先确定，预测一次需要临时计算，感觉类似KNN。

 　 参数学习算法的参数是固定的，一经学习得到不再改变。而非参数学习算法的参数并不固定，每次预测都要重新学习一组新的参数，并且要一直保留完整的训练样本集。当样本集很大时，局部加权回归的计算开销会很大，Andrew Moore提出的KD-tree方法可以在大      数据集上的计算更高效。

 

分类和logistic回归

 一般来说，回归不用在分类问题上，因为回归是连续型模型，而且受噪声影响比较大。如果非要应用到分类问题，可以使用logistic回归。

 logistic回归本质上是线性回归，只是在特征到结果的映射中加入了一层函数映射，即先把特征线性求和，然后使用函数g(z)来预测。g(z)可以将连续值映射到0和1上。

 

 logistic回归用来分类0/1问题，也就是预测结果属于0或者1的二值分类问题。这里假设了二值满足伯努利分布，也就是

由最大似然估计，求导，得到迭代公式如下：

可以看到与线性回归类似，只是换成了，而实际上就是经过g(z)映射过来的。

 

 

 

 

 

http://blog.csdn.net/suipingsp/article/details/42101139