6、激活函数

激活函数的主要作用是提供网络的非线性建模能力，如果没有激活函数，那么该网络仅能够表达线性映射，即便有再多的隐藏层，其整个网络跟单层神经网络也是等价的。

Sigmoid

Sigmoid函数的导数是其本身的函数，即f′(x)=f(x)(1−f(x))，计算非常方便，也非常节省计算时间。

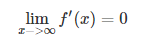
具有这种性质的称为软饱和激活函数。具体的，饱和又可分为左饱和与右饱和。与软饱和对应的是硬饱和, 即 f′(x)=0，当|x|>c，其中c为常数。
一旦输入落入饱和区，f′(x)f′(x) 就会变得接近于0，导致了向底层传递的梯度也变得非常小。此时，网络参数很难得到有效训练。这种现象被称为梯度消失。
此外，sigmoid函数的输出均大于0，使得输出不是0均值，这称为偏移现象，这会导致后一层的神经元将得到上一层输出的非0均值的信号作为输入。

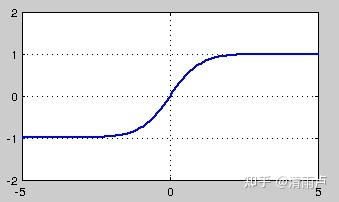
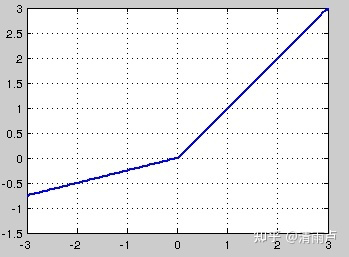
tanh

 

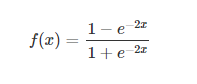
RELU

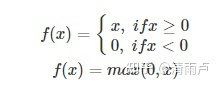
当x<0时，ReLU硬饱和，而当x>0时，则不存在饱和问题。所以，ReLU 能够在x>0时保持梯度不衰减，从而缓解梯度消失问题。

然而，随着训练的推进，部分输入会落入硬饱和区，导致对应权重无法更新。这种现象被称为“神经元死亡”。针对在x<0的硬饱和问题，Leaky-ReLU对ReLU做出相应的改进，使得