3、逻辑回归 && 正则化

Logistic 回归的本质是：假设数据服从Logistic分布，然后使用极大似然估计做参数的估计。

 

1、Logistic 分布

Logistic 分布是一种连续型的概率分布，其分布函数和密度函数分别为：

其中， 表示位置参数， 为形状参数。我们可以看下其图像特征：

 

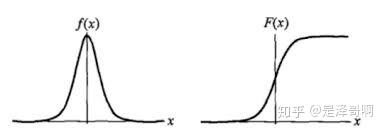
Logistic 分布的形状与正态分布的形状相似，但是 Logistic 分布的尾部更长，所以我们可以使用 Logistic 分布来建模比正态分布具有更长尾部和更高波峰的数据分布(此处需要对比下logistic分布和正态分布)。 在深度学习中常用到的 Sigmoid 函数就是 Logistic 的分布函数在 的特殊形式。

 

2、损失函数推导

逻辑回归在推导中使用的是先验概率最大化，构建的目标函数是正负样本概率连乘，然后在求解目标函数（也称之为似然函数）最大值的过程中 引入了对数log。就自然而然的得到了 形如交叉熵的表达式。可见 这里似然函数最大值求解 就等于 交叉熵函数的最小值求解

LR概率函数为：

在统计学中，常常使用极大似然估计法来求解，即找到一组参数，使得在这组参数下，我们的数据的概率最大。

设：

似然函数：

为了更方便求解，我们对等式两边同取对数，写成对数似然函数：（下方公式左侧应该加上ln）

在机器学习中我们有损失函数的概念，其衡量的是模型预测错误的程度，我们可以令损失函数为:

即在逻辑回归模型中，我们最大化似然函数和最小化损失函数实际上是等价的。

 

3、优化求解

逻辑回归的损失函数是：

随机梯度下降推导：

梯度下降是通过 J(w) 对 w 的一阶导数来找下降方向，并且以迭代的方式来更新参数，更新方式为 :

其中 k 为迭代次数。每次更新参数后，可以通过比较 小于阈值或者到达最大迭代次数来停止迭代。

 

4、正则化

正则化是一个通用的算法和思想，所以会产生过拟合现象的算法都可以使用正则化来避免过拟合。

在经验风险最小化的基础上（也就是训练误差最小化），尽可能采用简单的模型，可以有效提高泛化预测精度。如果模型过于复杂，变量值稍微有点变动，就会引起预测精度问题。正则化之所以有效，就是因为其降低了特征的权重，使得模型更为简单。

正则化一般会采用 L1 范式或者 L2 范式，其形式分别为 和 。

L1 正则化增加了所有权重 w 参数的绝对值之和逼迫更多 w 为零，也就是变稀疏（ L2 因为其导数也趋 0, 奔向零的速度不如 L1 给力了）。我们对稀疏规则趋之若鹜的一个关键原因在于它能实现特征的自动选择。一般来说，大部分特征 x_i 都是和最终的输出 y_i 没有关系或者不提供任何信息的。在最小化目标函数的时候考虑 x_i 这些额外的特征，虽然可以获得更小的训练误差，但在预测新的样本时，这些没用的特征权重反而会被考虑，从而干扰了对正确 y_i 的预测。

L2 正则化中增加所有权重 w 参数的平方之和，逼迫所有 w 尽可能趋向零但不为零（L2 的导数趋于零）。因为在未加入 L2 正则化发生过拟合时，拟合函数需要顾忌每一个点，最终形成的拟合函数波动很大，在某些很小的区间里，函数值的变化很剧烈，也就是某些 w 值非常大。为此，L2 正则化的加入就惩罚了权重变大的趋势。

总结：

L1 正则化就是在 loss function 后边所加正则项为 L1 范数，加上 L1 范数容易得到稀疏解（0 比较多）。L2 正则化就是 loss function 后边所加正则项为 L2 范数的平方，加上 L2 正则相比于 L1 正则来说，得到的解比较平滑（不是稀疏），但是同样能够保证解中接近于 0（但不是等于 0，所以相对平滑）的维度比较多，降低模型的复杂度。

 

5、为什么不用平方误差 : https://towardsdatascience.com/why-not-mse-as-a-loss-function-for-logistic-regression-589816b5e03c 参考交叉熵那一篇

假设目标函数是 MSE，即：

这里 Sigmoid 的导数项为： 

根据 w 的初始化，导数值可能很小（想象一下 Sigmoid 函数在输入较大时的梯度）而导致收敛变慢，而训练途中也可能因为该值过小而提早终止训练（梯度消失）。

另一方面，交叉熵的梯度如下，当模型输出概率偏离于真实概率时，梯度较大，加快训练速度，当拟合值接近于真实概率时训练速度变缓慢，没有 MSE 的问题。 

 

参考：

https://zhuanlan.zhihu.com/p/74874291