0、模型评价指标【AUC原理、roc曲线等】

分类模型评估：

指标	描述	Scikit-learn函数
Precision	AUC	from sklearn.metrics import precision_score
Recall	召回率	from sklearn.metrics import recall_score
F1	F1值	from sklearn.metrics import f1_score
Confusion Matrix	混淆矩阵	from sklearn.metrics import confusion_matrix
ROC	ROC曲线	from sklearn.metrics import confusion_matrix
AUC	ROC曲线下的面积	from sklearn.metrics import auc

回归模型评估：

指标	描述	Scikit-learn函数
Mean Square Error (MSE, RMSE)	平均方差	from sklearn.metrics import mean_squared_error
Absolute Error (MAE, RAE)	绝对误差	from sklearn.metrics import mean_absolute_error, median_absolute_error
R-Squared	R平方值	from sklearn.metrics import r2_score

混淆矩阵

对于一个二分类的模型，其模型的混淆矩阵是一个 $2 \times 2$

		Predicted condition	Predicted condition
		positive	negative
True condition	positive	True Positive	False Negative
False condition	negative	False Positive	True Negative

混淆矩阵比模型的精度的评价指标更能够详细地反映出模型的”好坏”。模型的精度指标，在正负样本数量不均衡的情况下，会出现容易误导的结果

True Positive：真正（TP），实际是正样本，预测为正样本。
False Negative：假负（FN），实际是正样本，预测为负样本。
False Positive：假正（FP），实际是负样本，预测为正样本。
True Negative：真负类（TN），实际是负样本，预测为负样本。

真正率(True Positive Rate,TPR)：TPR=TP/(TP+FN)，即被预测为正的正样本数 /正样本实际数

假正率(False Positive Rate,FPR) ：FPR=FP/(FP+TN)，即被预测为正的负样本数 /负样本实际数

假负率(False Negative Rate,FNR) ：FNR=FN/(TP+FN)，即被预测为负的正样本数 /正样本实际数

真负率(True Negative Rate,TNR) ：TNR=TN/(TN+FP)，即被预测为负的负样本数 /负样本实际数

Accuracy（准确率）：

正确预测的正反例数 / 样本的总数。

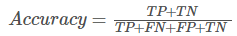
准确率是预测正确的结果占总样本的百分比，但很多项目场景不适用！最主要原因是样本不平衡。举个简单例子，一个总样本中，正样本占90%，负样本占10%，样本严重不平衡。这时候如果将全部正样本预测为正样本，即可达到90%的准确率。所以样本不均衡，准确率会失效。

Precision（精确率）：Percision = TP/(TP+FP)

正确预测的正例数 / 预测正例总数。可理解为查准率。在预测为正例的样本中，有多少实际为正。

召回率：Recall = TP / (TP+FN)

正确预测的正例数 / 实际正例总数。可理解为查全率。在实际为正例的记录中，有多少预测为正。

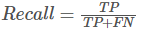
Recall越高，说明有更多的正类样本被模型预测正确，模型的效果越好。

F1 score：2/F1 = 1/Precision + 1/Recall

精确率和召回率的调和值。由于Precision和Recall是一对不可调和的矛盾，很难同时提高二者（不一定吧），故提出F1来试图综合二者，F1是P和R的调和平均。F1更接近于两个数较小的那个，所以精确率和召回率接近时值最大。很多推荐系统会用的评测指标。

对ROC曲线、AUC的理解

True Positive Rate（真阳率）、False Positive（伪阳率）：

$TPRate=\frac{TP}{TP+FN}$ （recall）
$FPRate=\frac{FP}{FP+TN}$

TPRate的意义是所有正样本中，预测类别为1的比例；FPRate的意义是所有负样本中，预测类别为1的比例。

按照定义，AUC即ROC曲线下的面积，而ROC曲线的横轴是FPRate（所有负样本中，预测类别为1的比例），纵轴是TPRate（所有正样本中，预测类别为1的比例），当二者相等时，即y=x，如下图:

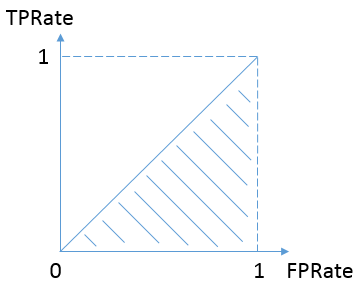
表示的意义是：对于不论真实类别是1还是0的样本，分类器预测为1的概率是相等的。

我们希望分类器达到的效果是：对于正样本，分类器预测为1的概率（即TPRate），要大于负样本被预测为类别1的概率（即FPRate），即y＞x，因此大部分的ROC曲线长成下面这个样子：

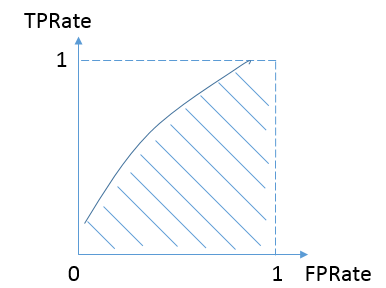
最理想的情况下，既没有真实类别为1而错分为0的样本——TPRate一直为1，也没有真实类别为0而错分为1的样本——FP rate一直为0，AUC为1，这便是AUC的极大值

如何得到roc曲线：

假设采用逻辑回归分类器，其给出针对每个实例为正类的概率，那么通过设定一个阈值如0.6，概率大于等于0.6的为正类，小于0.6的为负类。对应的就可以算出一组(FPR,TPR),在平面中得到对应坐标点。随着阈值的逐渐减小，越来越多的实例被划分为正类，但是这些正类中同样也掺杂着真正的负实例，即TPR和FPR会同时增大。阈值最大时，对应坐标点为(0,0),阈值最小时，对应坐标点(1,1)。

step1：假设已经得出一系列样本被划分为正类的概率，然后按照大小排序，下图是一个示例，图中共有20个测试样本，“Class”一栏表示每个测试样本真正的标签（p表示正样本，n表示负样本），“Score”表示每个测试样本属于正样本的概率。

step2：我们从高到低，依次将“Score”值作为阈值threshold，当测试样本属于正样本的概率大于或等于这个threshold时，我们认为它为正样本，否则为负样本。举例来说，对于图中的第4个样本，其“Score”值为0.6，那么样本1，2，3，4都被认为是正样本，因为它们的“Score”值都大于等于0.6，而其他样本则都认为是负样本。每次选取一个不同的threshold，我们就可以得到一组FPR和TPR，即ROC曲线上的一点。这样一来，我们一共得到了20组FPR和TPR的值，将它们画在ROC曲线的结果如下图：

随着样本数量增多，逐渐接近理想ROC曲线。

AUC计算方式：（如何证明2、3方式等价于1）

面积计算：矩形面积累加，计算复杂，基本不用。
统计正负样本对PK情况：统计一下所有的 M×N(M为正类样本的数目，N为负类样本的数目)个正负样本对中，有多少个组中的正样本的score大于负样本的score。当二元组中正负样本的 score相等的时候，按照0.5计算。然后除以MN。实现这个方法的复杂度为O(n^2)。实际也不会用。
rank求取：

降序rank--> 去掉（正，正）样本对数--> 求取比例

按概率从高到矮排个降序，对于正样本中score最高的，排序为rank_n，比它概率小的有M-1个正样本（M为正样本个数）， (rank_n- M) 个负样本。
正样本概率第二高的，排序为rank_n-1，比它概率小的有M-2个正样本，(rank_n-1 - M + 1) 个负样本。
以此类推正样本中概率最小的，排序为rank_1，比它概率小的有0个正样本，rank_1 - 1 个负样本。
总共有MxN个正负样本对（N为负样本个数）。把所有比较中正样本概率大于负样本概率的例子都算上，得到公式（rank_n - M + rank_n-1 - M + 1 .... + rank_1 - 1） / (MxN) 就是正样本概率大于负样本概率的可能性了。化简后（因为后面是个等差数列）得：

其实就是，按正样本score降序排列情况下，负样本pk失败的数目总数占所有样本对的比例。

AUC对正负样本比例不敏感的原因：

横轴FPR只关注负样本，与正样本无关；纵轴TPR只关注正样本，与负样本无关。所以横纵轴都不受正负样本比例影响，积分（求和）当然也不受其影响。

AUC概率意义：
随机挑选一个正样本和一个负样本，分类器将正样本排在前面的概率。

基于概率意义的到AUC的计算公式：

ROC-AUC 与 PR-AUC 的区别与联系：

https://zhuanlan.zhihu.com/p/349516115

参考：

https://www.cnblogs.com/keye/p/9367347.html

https://www.zhihu.com/question/39840928

https://www.jianshu.com/p/5e12cd6c3ed1

posted @ 2021-10-25 21:06 合唱团abc 阅读(513) 评论(0) 编辑收藏举报

刷新页面返回顶部

合唱团abc

0、模型评价指标【AUC原理、roc曲线等】

公告