目录:
- MAB的定义及意义
- MAB算法
- ε-Greedy 算法
- UCB算法
- 汤普森抽样
一、MAB(Multi-Armed Bandit)的定义及意义
1、在推荐系统中,为了解决准确率和多样性的平衡问题就是经典的Exploit-Explore【利用与探索问题】。其中,Exploit表示的是利用当前用户的信息或者利用当前最优结果,Explore是通过探索用户未知的可能存在潜在兴趣的内容。MAB主要解决的问题就是探索与利用之间寻找一个平衡,从而使得最终的收益最大化。
二、MAB的算法
1、ε-Greedy 算法
ε-Greedy就是一种很机智的Bandit算法:它让每次机会以ε的概率去“探索”,1-ε的概率来“开发”。
优点:
(1)能够应对用户兴趣的变化,能够以一定的概率ε探索用户未知的兴趣
(2)以1-ε概率充分利用当前的信息,选择最优的结果
在此基础上,又能引申出很多值得研究的问题:如ε应该如何设定呢?它应不应该随着时间而变?因为随着探索次数的增多,好的选择自然浮现得比较明显了。
ε大则使得模型有更大的灵活性(能更快的探索到未知,适应变化),ε小则会有更好的稳定性(有更多机会去“开发”)。
2、Upper Confidence Bounds算法 (UCB)
UCB 算法全称是 Upper Confidence Bound,即置信区间上界。它是计算每个臂的平均收益与该收益的不确定性来作为最终得分。公式如下:
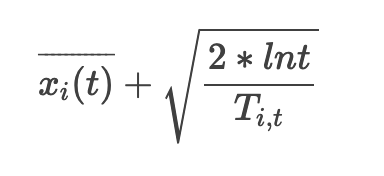
其中,i 表示当前的臂,t 表示目前的尝试次数,Ti,t 表示臂 i 被选中的次数。公式加号左边表示臂 i 当前的平均收益,右边表示该收益的 Bonus ,本质上是均值的标准差,反应了候选臂效果的不确定性,就是置信区间的上边界。
UCB 算法的流程如下:
(1)对所有臂先尝试一次
(2)按照公式计算每个臂的最终得分
(3)选择得分最高的臂作为本次结果
UCB 算法为什么有效?
(1)当一个臂的平均收益较大时,也就是公式左边较大,在每次选择时占有优势
(2)当一个臂被选中的次数较少时,即 Tit 较小,那么它的收益Bonus 较大,在每次选择时占有优势
3、Thompson Sampling 算法
每个臂是否产生收益的概率 p 的背后都对应一个 beta 分布。我们将 beta 分布的 α 参数看成是推荐后用户的点击次数, β 参数看成是推荐后用户未点击的次数。

汤普森算法主要流程:
(1)每个臂都维护一个 beta 分布的参数,获取每个臂对应的参数 α 和 β,然后使用 beta 分布生成随机数;
(2)选取生成随机数最大的那个臂作为本次结果;
(3)观察用户反馈,如果用户点击则将对应臂的 α 加 1,否则 β 加 1。在实际的推荐系统中,需要为每个用户保存一套参数,假设有m个用户,n个臂(选项可以是物品,也可以是策略), 每个臂包含 α 和 β 两个参数,所以最后保存的参数的总个数是 2mn。
为什么汤普森采样算法有效?
(1)当尝试的次数较多时,即每个臂的 α + β 的值都很大,这时候每个臂对应的 beta 分布都会很窄,也就是说,生成的随机数都非常接近中心位置,每个臂的收益基本确定了。
(2)当尝试的次数较少时,即每个臂的 α + β 的值都很小,这时候每个臂对应的 beta 分布都会很宽,生成的随机数有可能会比较大,增加被选中的机会。
(3)当一个臂的 α + β 的值很大,并且 α/(α + β) 的值也很大,那么这个臂对应的 beta 分布会很窄,并且中心位置接近 1 ,那么这个臂每次选择时都很占优势。



