本文主要介绍机器学习的基本知识，通过本文可以快速复习机器学习的主要内容。主要目录如下

一、特征工程

二、线性回归

三、逻辑回归

四、树模型

五、优化算法

六、激活函数

七、过拟合与欠拟合

---------------------------------------------------------------------------------------------------------------------------------------

一、特征工程

1、特征提取

（1）用户行为数据

（2）用户画像/标签

（3）Embedding：word2vec、glove、Node2Vec、DSSM、ELMO、GPT、BERT

（4）LDA

（5）TF/TFIDF

2、特征变换

（1）多项式变换

（2）PCA、SVD

（3）标准化

（4）离散化

3、特征选择

（1）与label无关的方法

  • 方差
  • 覆盖率

（2）与label有关的方法

  • 相关系数
  • 互信息：I(x,y)=H(Y)-H(Y|X),即在给定X条件下，Y变量不确定性程度缩减量。其中离散特征直接利用公式求解，连续变量则可以通过积分方式求解，另一种方式是先离散化，再按照上面公式求解。
  • IV值：IV=(P1-P0)*WOE=(P1-P0)*ln(P1/P0),其中P1表示正样本分布，P0表示负样本分布。属于二元分类特征的评价方式。
  • 卡方检验：假设自变量与因变量之间是相互独立，从而判断观测值与实际值之间的偏差。偏差往往用自变量与期望E之间的差值表示。偏差越大，假设不成立，则对立面成立。

（3）基于模型的方法

  • 基于L1正则项的特征选择
  • 基于树模型的特征重要性：其中这个特征重要性主要是在构建树的过程中，根据分裂特征的策略选择重要的特征依次进行分裂构建树。其中，分裂策略有：信息增益，信息增益率、gini指数等。

（4）递归消除法

  • 单因子构建模型的方式进行筛选

特征筛选的优点：

  • 降低过拟合的风险，提升算法的效果。实际工作中验证确实如此。
  • 提升算法的训练速度，降低计算开销。
  • 更少的特征意味着更好的可解释性。 

二、线性回归

  • 损失函数是均方误差——MSE。

三、逻辑回归

  • 损失函数-交叉墒损失函数

Question：为什么是交叉墒损失函数呢？

这个其实要从信息量的角度去考虑这个问题，首先我们来了解一下几个概念：

（1）信息量：衡量某个事件或者变量不确定性的程度

（2）信息墒：所有信息量的期望值，则可以表示如下所示：

　　　　　　　　　　

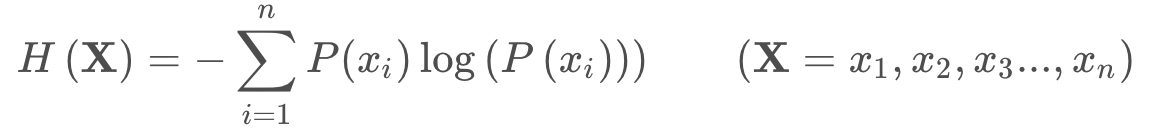
（3）相对墒（又称K-L散度）：简单理解是衡量两个概率分布之间的差异。也可以理解成是衡量同一个变量两个概率分布P(x) 和Q(x)之间的差异。其公式如下：

　　　　　　　　　　

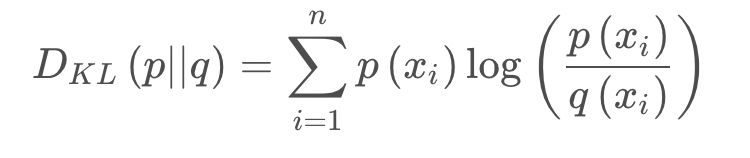
理论上逻辑回归的loss function应该是相对墒。But，当我们把相对墒进一步展开后可以发现：KL散度 = 交叉熵 - 信息熵

　　　　　　　　　　　　

 

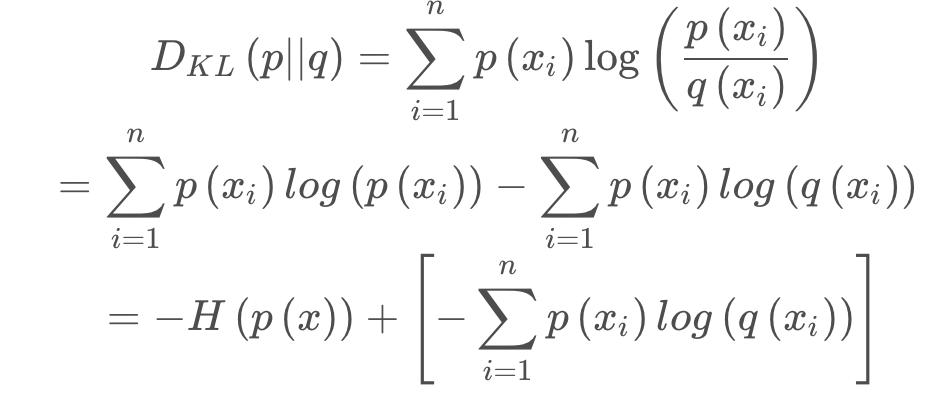
而我们的信息墒上面讲了是期望值，往往是一个常数。所以相对墒本质上就是交叉墒。

另一种推导方法：基于最大似然函数来进行推理。

不妨先用二分类作为我们的研究对象，则我们可以假设如下：对于某个样本输入正负样本的概率如下：

　　　　p(1|x)=h(x) 

　　　　p(0|x)=1-h(x)

则N个样本对应的整体的概率分布如下所示：

　　　　　　　　

 

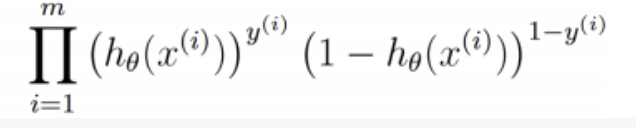
，此时由最大似然函数我们可知最大似然估计如下所示：

　　　　　　

 

上式，我们计算的是最大似然函数估计，得到的是最大值，而我们的损失函数往往是计算最小值，为了计算最小值，我们在上式最前面添加一个负号。则最终LR的损失函数如下所示：

　　　　　　　　　　

 

四、树模型

1、决策树算法：ID3、C4.5、CART

这三种决策树的算法主要区别是体现在构建树的过程中，衡量特征分裂的好坏的指标不同而已。具体的：

（1）ID3是以信息增益作为选择最优特征分裂的策略；所谓信息增益是根据某个特征分裂变换前后信息墒变换量。公式如下所示：

　　　　　　　　　　

 

　　缺点：

  • ID3没有预剪枝策略，容易过拟合
  • 信息增益容易偏向特征值较多的特征
  • 只能处理离散特征值，连续性的值一般需要做离散化之后才可以。

（2）C4.5

　　为了解决ID3的缺点作出相应的改进：

  • 首先C4.5是以信息增益率为选择分裂特征的策略。其公式如下所示：

　　　　　　　　　　

 

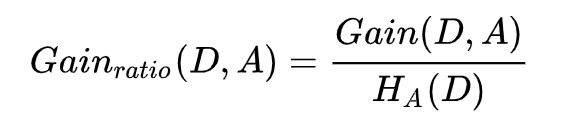
  • C4.5使用了预剪枝和后剪枝的方式来减少过拟合现象
    • 设置节点内样本数量限制，即某节点样本数量低于某阈值时，则不分裂，直接作为叶子结点
    • 节点分裂前后，对应准确率应有所提升，否则不分裂。
    • 后剪枝是遍历已生成的树，利用当前节点代替其子树，若正确率不降，则可以剪枝。否则不可以剪枝。
  • C4.5对连续特征进行自动离散化，首先对连续特征进行排序，再对相邻特征值作为离散化的值对特征进行离散化
  • C4.5也对缺失值做了相应的处理，但一般情况下，缺失值问题会在特征工程阶段已处理。

　　缺点：

  • ID3和C4.5都是多叉树，若用二叉树效果会更高
  • C4.5只能用户分类问题，回归问题无法适用
  • C4.5计算信息增益率时耗时比较严重，且需要对连续特征进行排序并离散化。

（3）CART

　　前面提到ID3和C4.5都是多叉树，且特征分裂计算墒效率较低。CART则是改用二叉树的方式来构建决策树，并且才用gini指数来选择分裂特征，从而提高算法的效率。其中gini指数如下所示：

　　　　　　　　　　　　

 

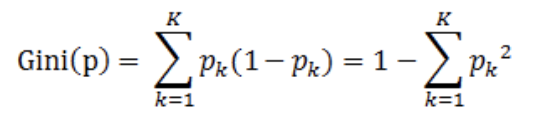
　　其中，pk表示样本分对的概率，1-pk表示样本分错的概率。基尼指数代表了模型的不纯度，基尼系数越小，不纯度越低，特征越好。

　　CART是分类回归树，既可以用来做分类模型也可以用来做回归模型，对于分类问题输出是类别较多的那个结果；对于回归问题，输出是叶子结点的均值或中位数。

 

2、随机森林：RF

　　上面我们讲到了决策树算法可以很好的对样本进行分类。而在实际应用中，决策树输出结果从精度上和稳定性上都存在不小的波动和差异。为了解决算法的波动性的问题，人们提出了一种集成的方法——Bagging方法。即利用多棵决策树来对目标问题进行建模。最终采取多票表决的形式进行预测。

优点：

  • 对样本和特征进行采样，分布式的构建多棵决策树
  • 对样本的异常值不敏感

3、GBDT、XGBOOST、LightGBM

（1）GBDT

　　GBDT也是一种集成学习方法——Boosting方法，该方法是递归的去构建每一棵树，并且每一棵树都是在拟合前一棵树的残差。这样的一种形式我们称之为Boosting方法。

GBDT与RF之间的差异：

相同点：

  • 都是CART二叉树构建的集成学习算法
  • 都可以用户分类和回归问题

不同点：

  • RF是bagging方法，GBDT是Boosting方法
  • RF可以并行构建二叉树，GBDT是串行方式构建回归二叉树
  • RF是降低模型的方差，GBDT是降低模型的误差
  • RF构建树时是随机抽样的样本和特征，GBDT是全部的样本
  • RF输出结果是多票表决，GBDT是结果求和
  • RF泛化能力较强，GBDT容易过拟合。

（2）XGBOOST

XGBOOST算法是针对GBDT从工程上、和算法精度上引入二阶偏导数和正则项 进行优化，XGBOOST算法中对应损失函数如下所示：

　　　　　　       其中，

　　　　　　　　

l表示损失函数，一般是MSE和交叉墒等。第二项是正则项，可以控制树的复杂度，防止过拟合。在损失函数求解的过程中，对损失函数使用了泰勒展开，并保留了前三项（即保留了二阶偏导数）。如下所示：

　　　　　　　　　　　　

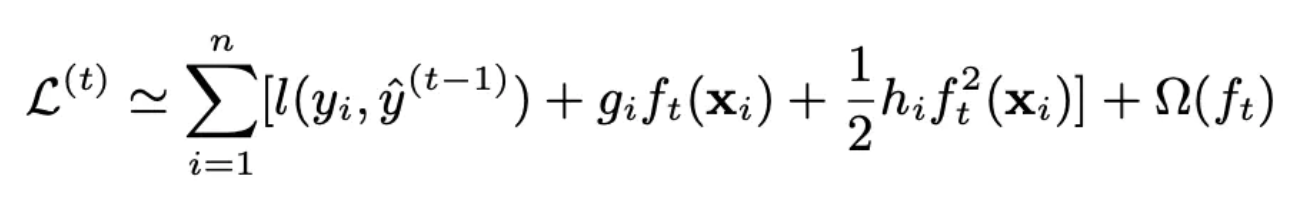
XGBOOST的叶子节点的权重：

　　　　　　　　　　　　　　　　　　　　　　

XGBOOST与GBDT对比
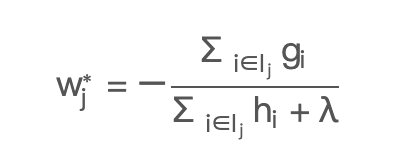
  • 模型优化上：
    • 基础模型优化：
      • gbdt用的是cart回归树作为基础模型，xgboost还可以用线性模型，此时相当于带有L1和L2正则项的逻辑回归（分类问题）和线性回归（回归问题）
    • 损失函数优化：
      • gbdt对loss是泰勒一级展开，xgboost是泰勒二级展开
      • gbdt 损失函数没有正则，xgboost在损失函数中引入 叶子结点个数 和 L1、L2正则项
    • 特征分裂的优化：
      • xgboost实现了一种分裂节点寻找的近似算法【近似直方图算法】，用于加速和减少内存消耗，而不是gbdt的暴力搜索
      • 节点分割算法解决了梯度值方向的问题，gbdt分割用了购物车的方法进行加权
      • XGBoost对缺失值不敏感，能自动学习其分裂方向
    • 其他正则化的优化：
      • 特征采样
      • 样本取样
  • 工程优化上：
    • xgboost在对特征进行了分块预排序，对特征预先进行排序并保存为block，后续迭代中重复使用，减少计算；同时在计算分割点时，可以并行计算
    • 缓存感知、核外计算
    • 支持多元化计算可以运行在MPI，YARN上，受益基础支持容错的多元化通信框架rabbit、
XGBOOST与LightGBM对比
  • XGBoost采用预排序，在迭代之前，对结点的特征做预排序，遍历选择最优分割点，数据量大时，贪心法耗时，LightGBM方法采用histogram算法，占用的内存低，数据分割的复杂度更低，但是不能找到最精确的数据分割点。同时，不精确的分割点可以认为是降低过拟合的一种手段。
  • LightGBM借鉴Adaboost的思想，对样本基于梯度采样，然后计算增益，降低了计算
  • LightGBM对列进行合并，降低了计算
  • XGBoost采样level-wise策略进行决策树的生成，同时分裂同一层的节点，采用多线程优化，不容易过拟合，但有些节点分裂增益非常小，没必要进行分割，这就带来了一些不必要的计算；LightGBM采样leaf-wise策略进行树的生成，每次都选择在当前叶子节点中增益最大的节点进行分裂，如此迭代，但是这样容易产生深度很深的树，产生过拟合，所以增加了最大深度的限制，来保证高效的同时防止过拟合。

（3）LightGBM《LightGBM：A HIghtly Efficient Gradient Boosting Decision Tree》

　　lightGBM算法的是在GBDT的基础上进行优化的。我们知道GBDT的缺点主要原因是GBDT在构建树的过程中需要对每个特征进行全量扫描，找到最佳的分割点。这给算法带来比较低效的性能。
而LightGBM在此基础上针对这个做了优化，主要表现在两个方面：
  • 尽量减少样本数据
    • 通过GOSS（gradient of sildes sampling）的方法，即对样本按照梯度的大小进行降序排序，这里梯度比较小的样本是模型已经学习到了，所以对应的误差小，即梯度小。
    • GOSS的思想就是保留那些没有学习到的样本（梯度比较大的样本）
    • 对梯度较小的样本进行随机采样的方法来保留整体样本的分布。这里面会涉及到两个参数：一个梯度大的样本采样比例a；另一个是梯度小的样本采样比例b。
  • 尽量减少特征，减少特征需要回答两个问题：1、如何合并？2、那些特征需要合并？则对应的方法如下：
    • 合并特征：如何合并特征，论文提出的方法是扩展特征的边界。比如：特征A对应的边界是(0,10],特征B的边界是(0,20],则合并的 方法是在特征B的基础上+10，再融合特征A得到特征C的边界是(0,30]。
    • 哪些特征应该合并呢？

　　　　　　方法是：通过构建有颜色的图的方法。即将特征作为顶点，如果两个特征不会相互排斥则构建一条边。不会相互排斥的特征非常少，一般情况算法是容忍一定比例的冲突。 

五、优化算法，参考文献：https://arxiv.org/pdf/1609.04747.pdf

　　这里主要讲一下深度学习当中应用到的优化算法，主要是将随机梯度下降算法的家族及其变种，变种主要表现两个方面：

（1）一个是从学习率的角度，通过改变学习率来提升优化算法的效果；

（2）另一个是从更新速度的角度去提升优化算法的更新速度，如动量。

  • SGD 随机梯度下降：即每次根据一个样本去更新模型的参数。缺点：无法得到全局最优，且对异常样本非常敏感

　　　　　　　　　　　　　　　　　　

 

 　　　　其中，（xi，yi）表示样本i。

  • 批量梯度下降：即每次根据全量的样本去更新模型的参数。缺点：算法复杂度较高，需要较大的内存支撑

　　　　　　　　　　　　　　　　 

  • mini-batch梯度下降：即每次根据一小批量的样本进行模型参数更新。该方法综合了SGD和批量梯度下降的优点。

　　　　　　　　　　　　

 

　　　　　　其中，n表示bacth的大小。

  • Momentum：带有动量的梯度下降算法，更新公式如下所示：

　　　　　　　　　　

 

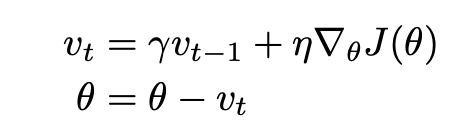
　　　　其中，Vt-1表示上一次的更新速度，即动量。

  • Adagrad：对学习率进行修改，每个样本的学习率都不一样。错误的样本对应的学习率较大。其公式如下：

　　　　　　　　　　　　　　　　　　　　　　

 

 　　　　　　　　　　　　　　　　　　　　　

 

　　将上面两个式子合并可得到如下所示：

　　　　　　　　　　　　　　　　　　　　　　　　

 

 

 

  • Adadelta：是在Adagrad基础上进一步扩展。
  • RMSprop：该方法是结合momentum和adagrad方法的各自的优点进行融合的方法。其公式如下所示：

　　　　　　　　　　　　　　　　

 

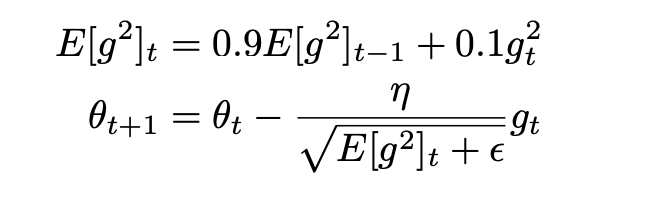
　　　　　　上式中[g]t-1是表示的上次更新的速度，即动量。生成新的参数E，从而来调整当前的学习率。

  • Adam：上面RMSProp方法中，并没有完全把动量引入进来，所以Adam是在RMSProp基础上完全把动量引入进来。其公式如下所示：

　　　　　　　　　　　　　　　　　　　　

　　　　　　　　　　　　　　　　　　　　　　

 

　　　　　　　　　　　　　　　　　　　　　　　

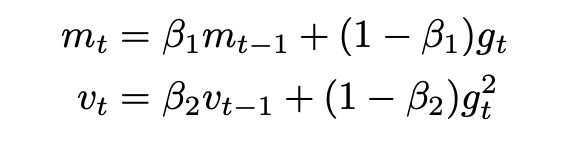
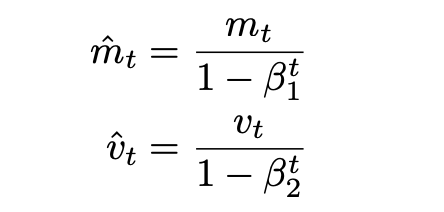
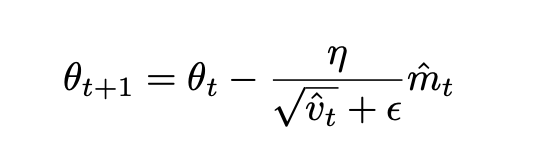
其中，vt就是更新速度，mt是动量。 

六、激活函数

  • sigmoid函数，其表达式及图像如下所示

 

　　　　　　　　　　　　　　　　　　　　　　

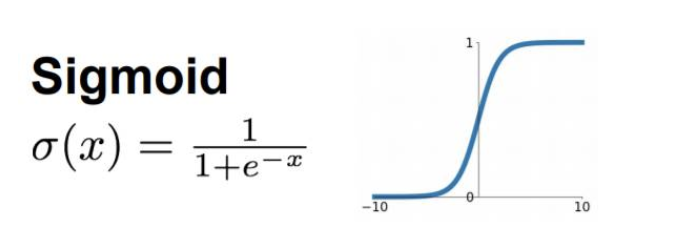
　　　　从图像当中我们可以看出，当x较大或者较小时，sigmoid对应的梯度趋近0，容易导致梯度消失。 

  • Relu函数

　　　　　　　　　　　　　　　　　　　　  

 

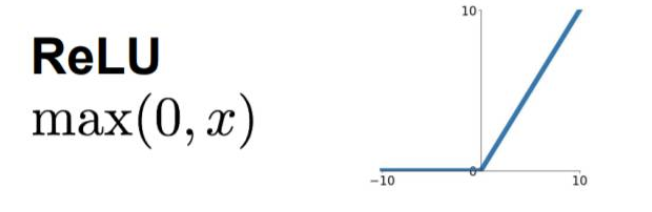
　　当x>0时，对应的梯度恒等于1，当x<0时，梯度等于0，导致神经元无法更新。但实际场景中，往往一般不会出现x小于0的情况。

  • ELU

　　　　　　　　　　　　　　　　　　　　　　

 

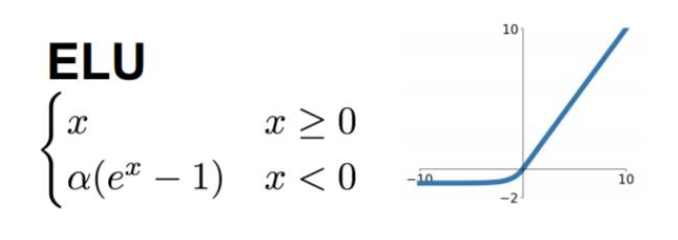
　　其融合sigmoid和ReLU的优点，左侧具有软饱和性，右侧具有硬饱和性。

 

七、过拟合与欠拟合

（1）过拟合：当模型在训练集中表现效果很好，在测试集中表现非常差。

  • 模型角度
    • 添加正则项：L1正则和L2正则：其中L1正则是y=｜X｜，在x=0处不可导，且在x=0使得结果最小。L2正则y=||x||^2。求导之后还有一次项，对参数更新具有一定的泛化作用。
    • early stopping
    • 结合多种模型结果：
      • Bagging训练多个模型进行多票表决
      • Boosting训练减少网络层数和神经元个数：如dropout
  • 数据角度
    • 获取更多的训练数据
    • 增加一定比例的噪声数据来提升模型的泛化能力

（2）欠拟合：当模型在训练集表现效果较差时。

  • 模型角度
    • 增加模型的复杂度，如采用boosting方法，增加网络的层数和神经元个数
    • 选择算法优化精度较高的模型
  • 数据角度
    • 分析错例的原因，挖掘有效的特征
    • 增加更多的训练数据

八、RNN与LSTM原理

RNN是递归神经网络，其网络结构如下所示：

　　　　　　

　　　　　　　　　　　　

 

BP算法：

　　RNN的训练：循环递归神经网络的训练类似传统的神经网络的训练，也是使用反向传播算法，但是有所变化。因为循环神经网络在所有时刻的参数是共享的，但是每个时刻输出的梯度不仅依赖当前时刻的计算，还依赖之前时刻的计算，然后将梯度进行相加。我们称之为BPTT。

　　这与我们深度前馈神经网络中使用的标准反向传播算法基本相同。主要的差异就是我们将每时刻W的梯度进行相加。在传统的神经网络中，我们的层之间并没有共享参数，所以不需要进行相加。

结论：

　　RNN的关键点之一就是他们可以用来连接之前的信息到当前的任务上。例如使用过去的视频片段来推测当前段的理解。但是当相关的信息和当前待预测位置之间的间隔变得非常大时，RNN会丧失学习较远信息的能力。所以利用BPTT算法训练出来的RNN循环神经网络很难学习长期依赖，原因在于梯度消失和爆炸问题。所谓梯度消失和爆炸的原因是因为BPTT在求梯度的过程中，由于当前时刻是依赖上一时刻的输出，则对应的梯度是累乘的，梯度有可能是大于1或者小于1，累乘之后有可能出现梯度爆炸和消失的现象。于是人们就设计出来了LSTM。

LSTM

LSTM网络结构如下所示：主要包含三个门：遗忘门、输入门和输出门

　　　　　　　　　　　　

 

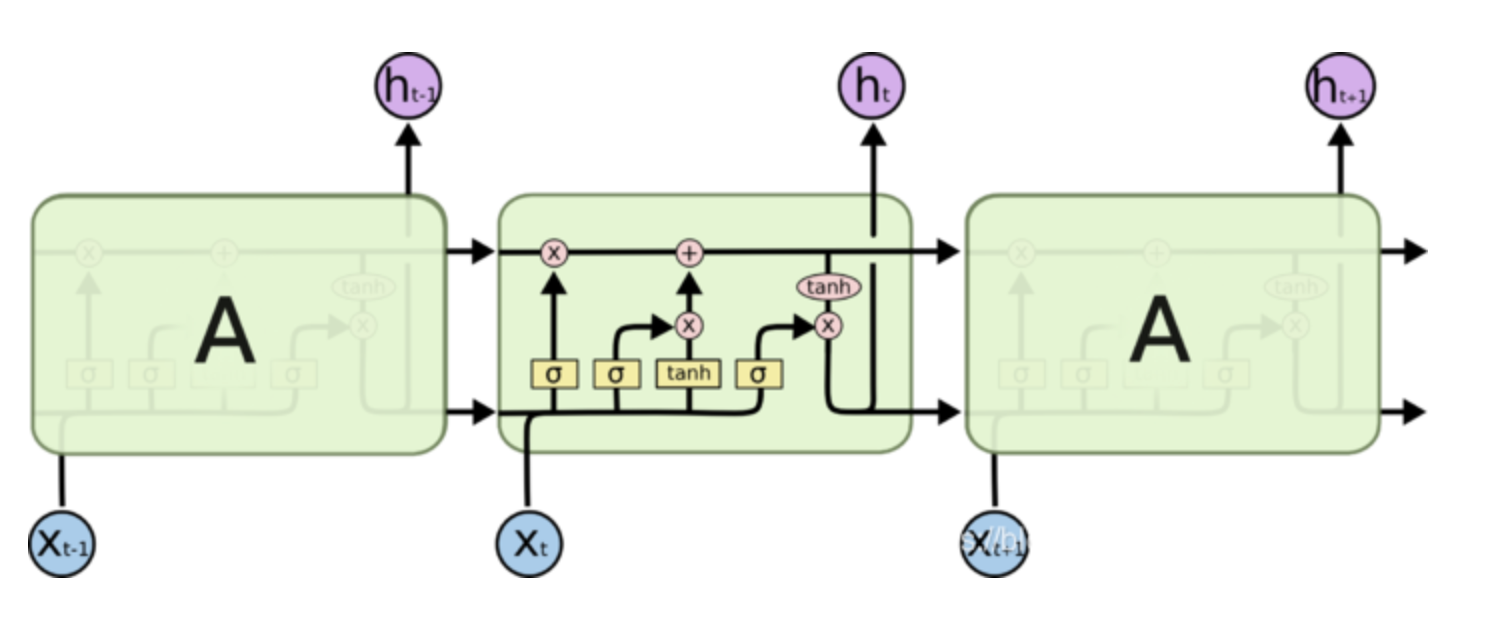
遗忘门：主要决定从cell中丢弃多少信息，主要通过控制遗忘门的sigmod来决定丢弃多少信息。

　　　　　　　　　　

 

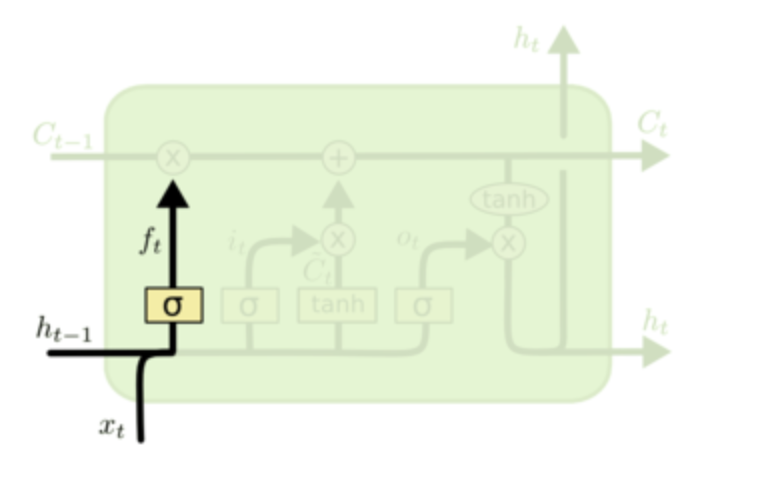
输入门：主要决定有多少新的信息加入到cell中。同样是通过sigmod函数来控制多少信息增加到cell中。

　　　　　　

 

输出门：决定最终输出什么到下一个状态。同样也是通过sigmod来确定。