1.学习总结
1.1图的思维导图
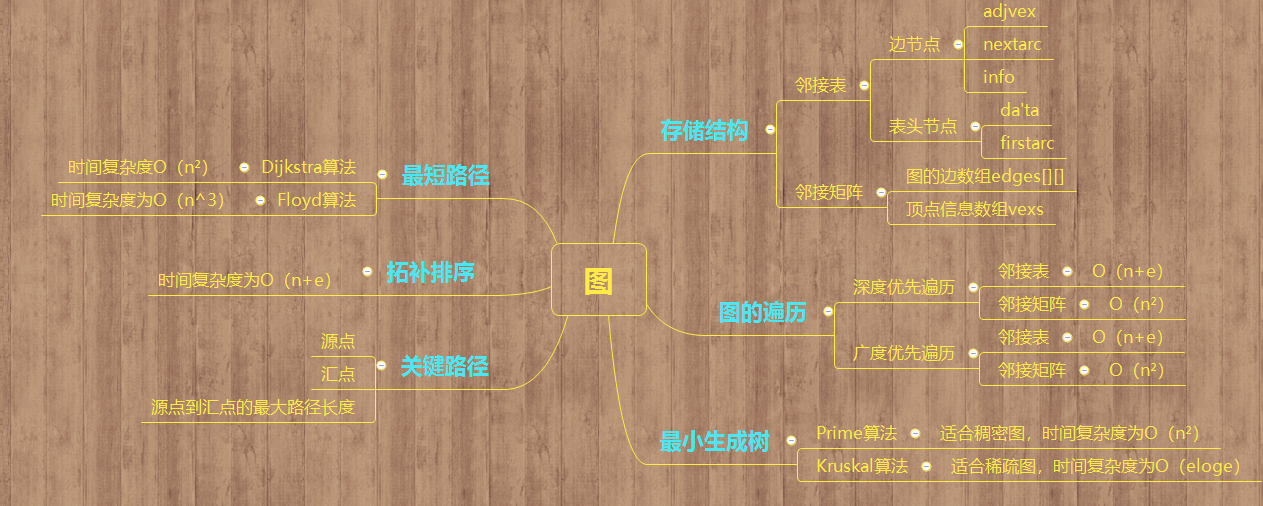
1.2图结构学习体会
- 深度优先遍历:从图的某个顶点出发,访问图中的所有顶点,且使每个顶点仅被访问一次。这一过程叫做图的遍历。
深度优先搜索的思想:
①访问顶点v;
②依次从v的未被访问的邻接点出发,对图进行深度优先遍历;直至图中和v有路径相通的顶点都被访问;
③若此时图中尚有顶点未被访问,则从一个未被访问的顶点出发,重新进行深度优先遍历,直到图中所有顶点均被访问过为止。
数组表示:查找所有顶点的所有邻接点所需时间为O(n2),n为顶点数,算法时间复杂度为O(n²) - 广度优先遍历: 广度优先搜索的思想:
① 访问顶点vi ;
② 访问vi 的所有未被访问的邻接点w1 ,w2 , …wk ;
③ 依次从这些邻接点(在步骤②中访问的顶点)出发,访问它们的所有未被访问的邻接点; 依此类推,直到图中所有访问过的顶点的邻接点都被访问;
数组表示:查找每个顶点的邻接点所需时间为O(n2),n为顶点数,算法的时间复杂度为O(n²) - Prim算法: Prim算法的思想:
① 清空最小生成树,随机选一个顶点加入树中
②选择那些一端顶点在树中,另一端顶点不在树中的边,选择一条权值最小的边,将其两个顶点加入树中
③重复步骤2,直到所有顶点都加入树中
时间复杂度为O(n²) - Kruscal算法: Krucal算法的思想:
① 将每个顶点放入其自身的数据集合中
② 按照权值的升序来选择边。当选择每条边时,判断定义边的顶点是否在不同的数据集中。如果是,将此边插入最小生成树的集合中,同时,将集合中包含每个顶点的联合体取出,如果不是,就移动到下一条边
③重复步骤2,直至所有顶点都在一棵树中
时间复杂度:O(e²) - Dijkstra算法: Dijkstra算法思想:
① 从特定起点(顶点s)出发
②引入两个集合S和U,集合S存放起点s,集合U存放除顶点s以外所有未求出的顶点(及其到起点的距离)
③更新U中各个顶点到起点s的距离,之后更新集合U中顶点的距离,选取最小路径长度顶点,重复步骤2和3
时间复杂度:O(n²) 堆优化后O(nlogn) - 拓补排序算法:拓补排序算法思想:
① 从有向图中选取一个入度为0的顶点并输出
②从图中删去这个顶点,并且删除这个顶点相关的边
③重复步骤1和2,直到有向图没有顶点
时间复杂度:O(n²)
2.PTA实验作业
2.1题目1:图着色问题
2.1.1设计思路
初始化顶点v,边数e,颜色数k,数组color存放配色,set容器s,vector容器vec存放
输入v,e,k
for i=0 to e-1
输入两个顶点a和b
将b插入容器vec[a]的尾部,将a插入容器vec[b]的尾部
end for
输入需要验证的配色和个数number
while(number--)
将容器s清空
for i=1 to v
输入v个顶点配色,将输入的顶点插入容器s中
end for
如果容器s的长度不等于颜色数k,flag=0
遍历vec容器,如果数组color和vec容器颜色相同,退出遍历并令标志遍历flag=0
如果flag=0,输出No,否则输出Yes
2.1.2代码截图

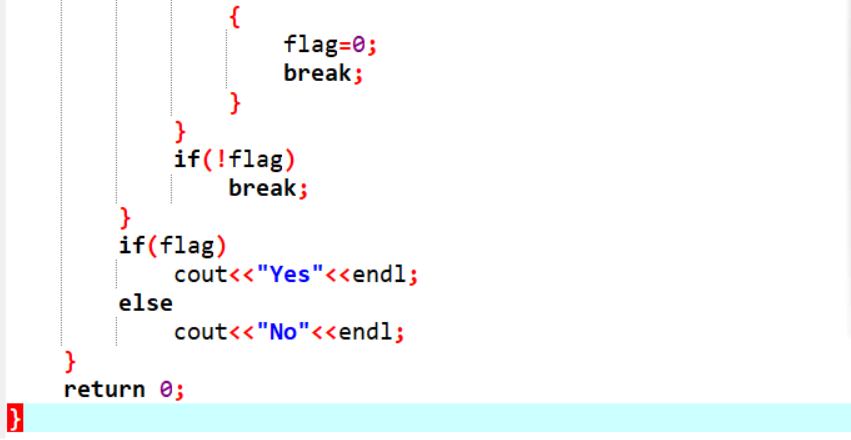
2.1.3PTA提交列表
- 刚开始的全部错误是因为输出将Yes和No写成了yes和no


- 全局变量flag不能再while循环里面重置为0,导致标志变量一直递增,只能输出No
2.2题目2:公路村村通
2.2.1设计思路
初始化循环遍历i,j,sum存放最小路径,数组cost存放顶点间的路径长度,二维数组G存放邻接矩阵
访问第一个顶点,并将其路径置为-1
for i=1 to v
初始化最小值min=32767,临时下标k=-1
for j=1 to v
if(j下标的顶点已访问且cost[j]<min)
替换cost[j]的值且标记下标
if(序列为无序(k!=-1))
计算路径长度sum+=cost[k]并访问
for j=1 to v
if(G[k][j]<cost[j])
替换cost[j]的值
遍历所有顶点,如果cost数组没有全部访问过,返回-1,否则返回sum
2.2.2代码截图

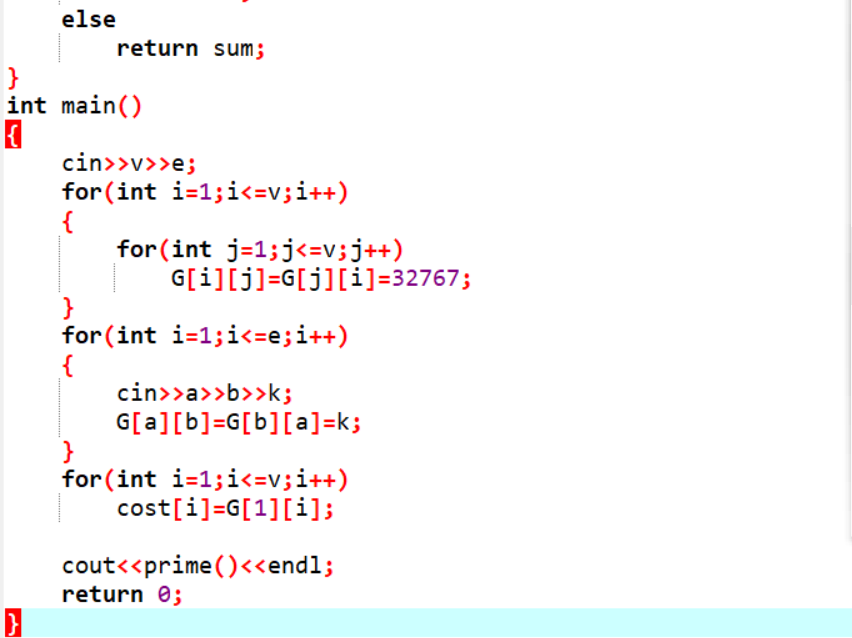
2.2.3PTA提交列表

- 这里的下标应该是j不是k,如果下标为k会修改掉刚找到的最小权值,导致最终输出的权值不是最小
2.3题目三:修建道路
2.3.1设计思路
初始化循环变量i,j,路径长度和sum=0,数组visited存放顶点访问信息,
cost数组存放顶点之间的路径长度,二维数组G存放顶点之间的信息
访问第一个顶点并令其路径长度未0
for i=1 to v
初始化最小值min=32767,临时下标k=1
for j=1 to v
if(j下标的顶点未访问且路径长度小于min)
替换最小值并标记下标
计算路径长度和sun+=cost[k],并访问k下标的顶点
for j=1 to v
if(j下标顶点为访问且G[k][j]<cost[j])
替换cost[j]的值
返回sum
2.3.2代码截图
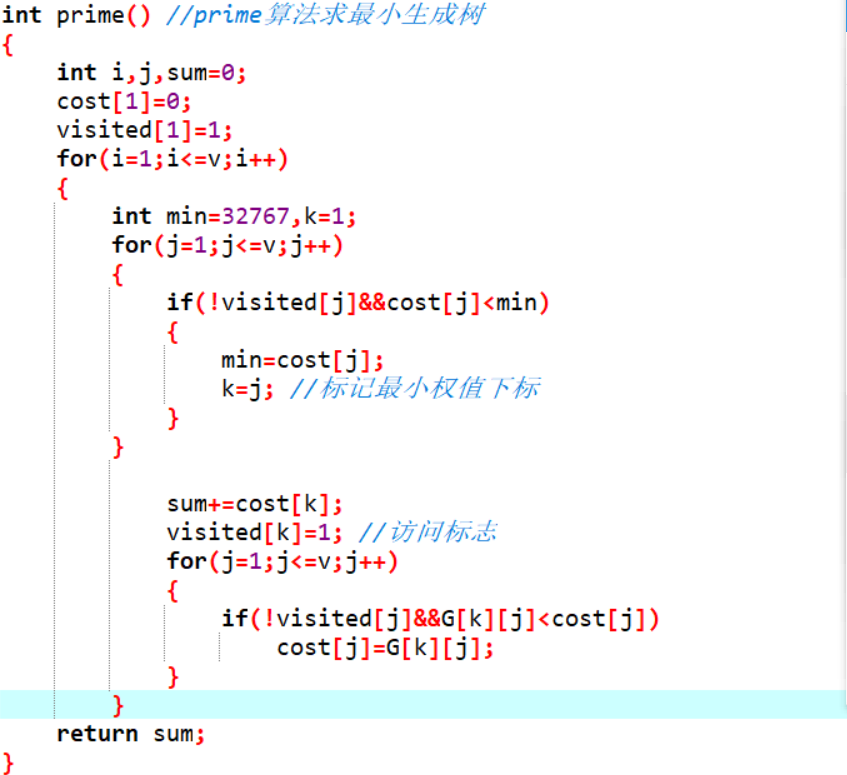

2.3.3PTA提交列表

- 这边忘了s的访问标志,导致后面判断是否访问过该顶点错误
3.截图本周题目及的PTA最后排名
3.1PTA排名

3.2我的总分
268
4.阅读代码
匈牙利算法之男孩女孩配对(一个例子)
bool find(int x){
int i,j;
for (j=1;j<=m;j++){ //扫描每个妹子
if (line[x][j]==true && used[j]==false)
//如果有暧昧并且还没有标记过(这里标记的意思是这次查找曾试图改变过该妹子的归属问题,但是没有成功,所以就不用瞎费工夫了)
{
used[j]=1;
if (girl[j]==0 || find(girl[j]))
{
//名花无主或者能腾出个位置来,这里使用递归
girl[j]=x;
return true;
}
}
}
return false;
}
int main()
{
for (i=1;i<=n;i++)
{
memset(used,0,sizeof(used)); //这个在每一步中清空
if find(i) all+=1;
}
}
- 基本思想:二分图中找增广路径,用增广路径求二分图最大匹配的算法
- 学习地方:博主的例子写得真的是简单粗暴易懂,选择没匹配过的两个点进行连接,如果后面的点选择到了匹配的边,则消除之前的匹配关系,回溯回去,给被消除匹配关系边的点继续寻找未匹配的边,直到这样的点消失
附上链接:https://blog.csdn.net/cillyb/article/details/55511666




 posted on
posted on

