1.学习总结
1.1树结构思维导图

1.2树结构学习体会
刚开始学树觉得很难,学到现在依然觉得不简单,这是一种应用很广的数据结构,很多算法用树可以很巧妙的处理
难题:递归建树递归出口容易搞错,半天找不出问题所在;非递归建树(队列建树)时,判断条件经常经常漏掉,导致段错误(这次上机考就是这样);平时的PTA题目有思路但具体代码实现不怎么会写,对数的理解还不够
应用:哈夫曼编码、家谱族谱记录、朋友圈、广度深度搜索等
2.PTA实验作业
2.1题目一:表达式树
2.2设计思路
**建树**
创建一个char类型存放逻辑运算符的栈op和一个BTree类型存放数字的栈st
创建BTree类型的结bt和leaf
先将#入栈
遍历str函数
如果为数字
为叶子结点leaf申请空间,并将str的值赋予它,同时将它入到st栈中
如果为逻辑运算符
先判断op栈顶运算符和str运算符优先级大小
若op大,则将op栈和st栈出栈,并将栈op字符作为双亲、栈st的数字遵循先右再左的顺序建树
若op小,则继续入栈
若遇到括号匹配,优先出栈
将op栈剩余的运算符全部出栈
方法同上,先右再左的原则建树
最后将栈st顶的字符赋予T,作为其根节点
**计算**
创建BTree类型的栈s存放T的所有结点
创建double类型的栈result存放计算结果
后序遍历树T,遇到运算符,出栈左右孩子结点作相应的逻辑运算操作,得出的结果覆盖原本运算符的位置
遍历到树空时,返回栈result顶的值,即为表达式的值
2.3代码截图

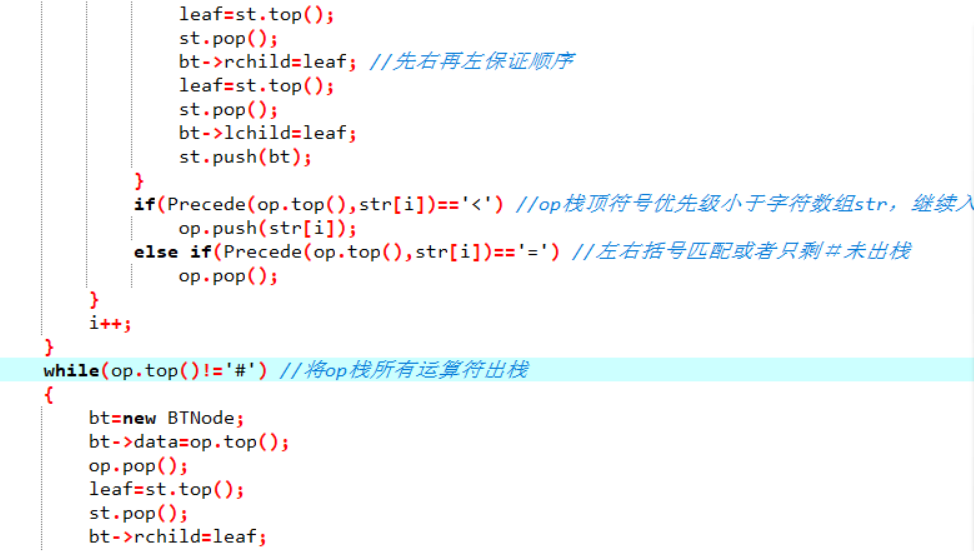
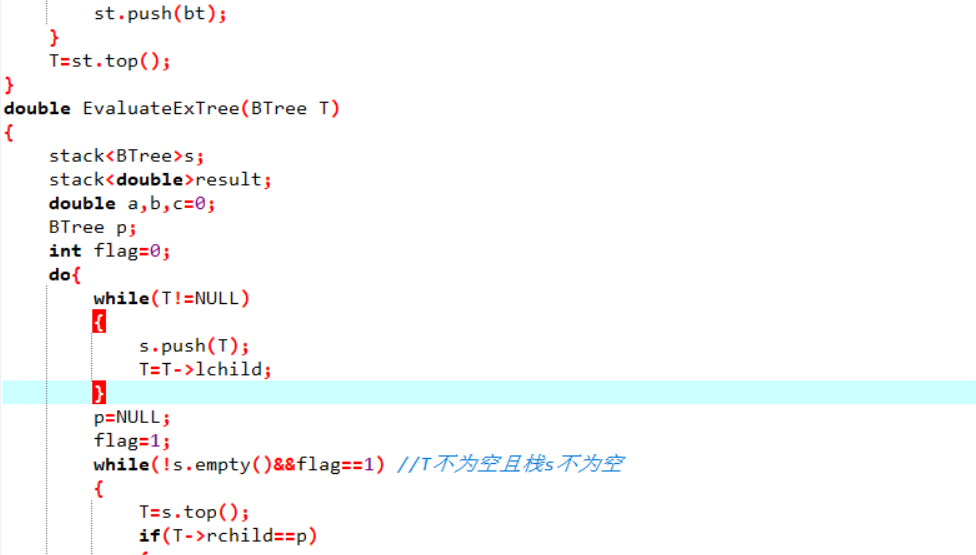
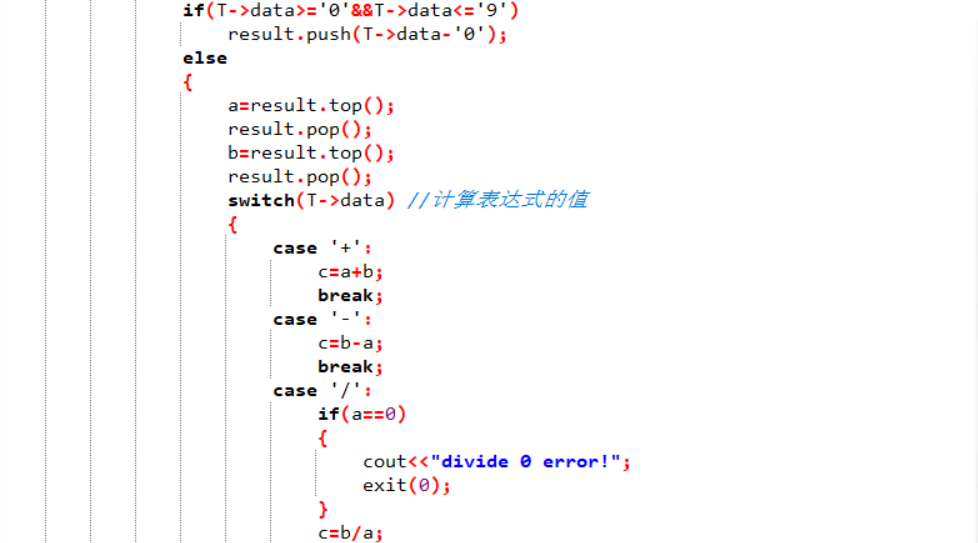

2.4PTA提交列表截图
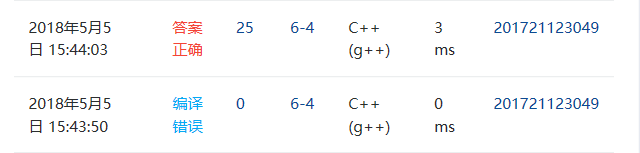
基本没有什么大问题,就是按照上课说的方法来写代码,交的时候多交了一些函数导致编译错误
2.2题目二:修理牧场
2.2设计思路
申请一个优先队列q
输入木头要切成的段数n和每段的长度m
将m压入优先队列q
每次取最小两个数出队,相加之后再入队
sum记录每次两个权值最小的数相加之和
出队到队列q为空,再输出sum即为最小花费
2.3代码截图

2.4PTA提交列表截图
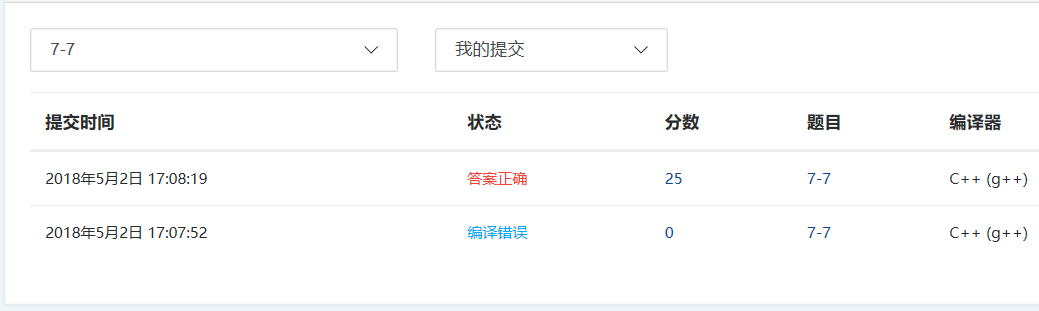
编译错误是因为队列q去栈顶函数top没括号导致
ps:用优先队列做的复杂度远比用树做低,而且更加简单易懂
2.3题目三:二叉树叶子结点带权路径长度和
2.2设计思路
**建树:**
建立BTree类型的栈q
建立BTree类型的树T
直接从第二个数开始判断是否为#号
若为#号,则该树为空树
否则创建新的左右孩子节点,将数组str[1]的值赋予树T根节点,并将BT入队
while(队列q不为空)
T取q队头后将其出队
如果T不为空树,构建左子树,并将左节点入到队q
当左结点构建完毕,如果T不为空树,构建右子树,并将右节点入到队q
当数组str遍历完毕后退出循环
**计算wpl:**
设置静态局部变量sum存放wpl的值
如果BT不为空树且遍历到叶子结点
sum的值为上次sum的值加上当前结点权值BT->data*结点深度weight
递归遍历所有叶子结点,重复上述步骤直到遍历完整棵树
2.3代码截图
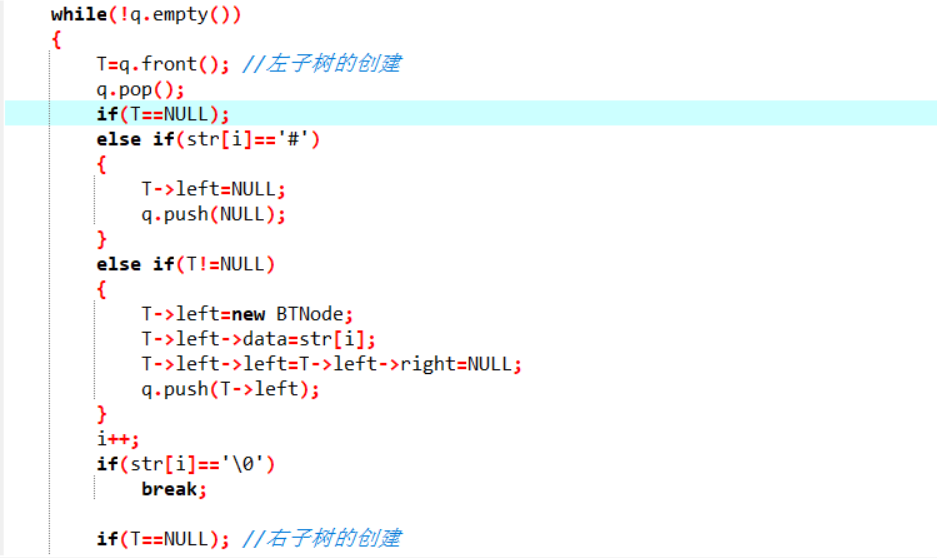
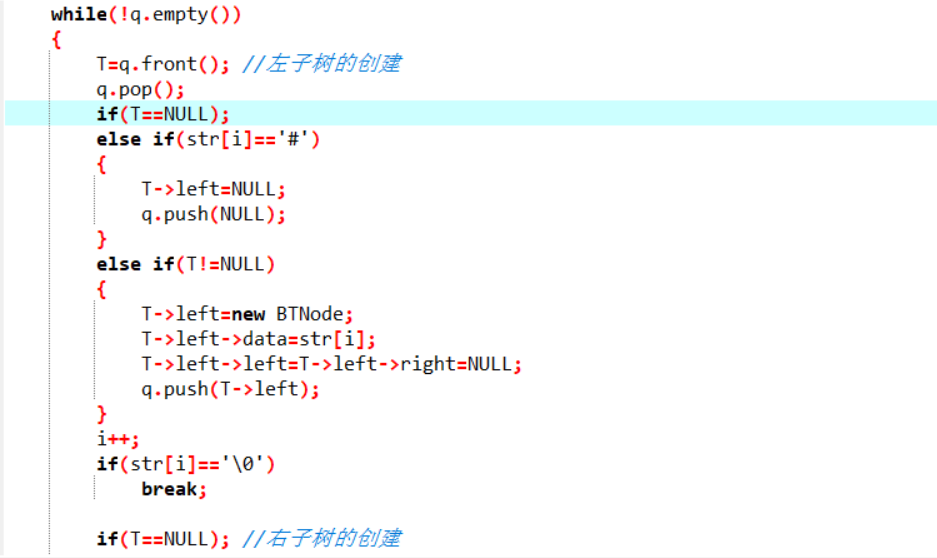

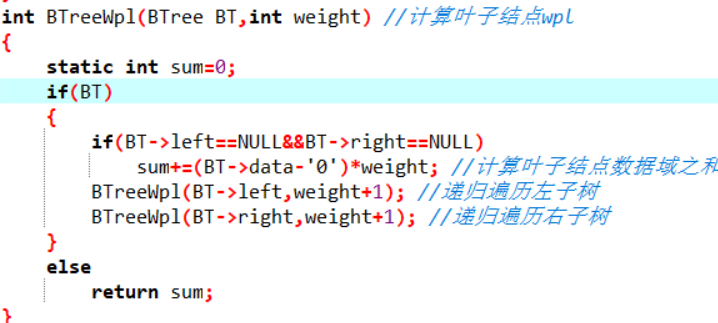
2.4PTA提交列表截图
五分的原因:建树构建右子树时函数没写完整


十五分的原因:计算wpl时,非叶子结点的条件写成了if(BT->left!=NULL||BT->right!=NULL),逻辑关系就混乱了,不知道是只有左子树为空还是右子树为空亦或是两者皆为空,导致sample 1过了,sample2没过

3.截图本周PTA题目集的最终排名
3.1PTA排名

3.2最终得分
230
4.阅读代码
部分代码
int main()
{
while (1)
{
int N, i;
cin >> N;
cin.get();
if (N == 0)break;
int L;
cin >> L;
cin.get();
Tree T = CreatTree(N);
for (i = 0; i < L; i++)
{
Initialize(T);
if (Judge(T, N))cout << "Yes" << endl;
else
cout << "No" << endl;
}
FreeTree(T);
}
return 0;
}
bool Check(Tree T, int tmp)
{
if (T->flag)
{
if (tmp > T->Data)return Check(T->Right, tmp);
else if (tmp < T->Data)return Check(T->Left, tmp);
else
return false;
}
else
{
if (T->Data == tmp)
{
T->flag = 1;
return true;
}
else
return false;
}
}
bool Judge(Tree T,int N)
{
int tmp;
int flag = 0;
cin >> tmp;
cin.get();
if (T->Data == tmp)
T->flag = 1;
else
flag = 1;
for(int i=1;i<N;i++)
{
cin >> tmp;
cin.get();
if (!flag && !Check(T, tmp))flag = 1;
}
if (flag == 1)return false;
else true;
}
功能:判断是否为同一棵二叉搜索树
优点:递归遍历输入的二叉树数据,检查是否和初始二叉树相同,代码量少,阅读起来思路较清晰。我刚开始的思路是,递归建树之后,再中序遍历(如果二叉树一样序列会相同),对比题目给的序列,相同则输出yes,不同输出no,后来发现这样做时间复杂度比较高
5.代码Git提交记录截图




 posted on
posted on

