博客作业03--栈和队列

1.学习总结

1.1逻辑结构、存储结构、栈、队列等关键知识点

栈：能够实现多栈共享；删除数据在表尾进行操作；遵循“先进后出”原则；应用场景一般在括号问题的求解，表达式的转换和求值，函数调用和递归实现，深度优先搜索遍历等；栈分为顺序栈和链栈，其中顺序栈需要提前申请存储空间，但顺序栈删除和插入元素不需要移动元素，而链栈不需要提前申请空间，可以合理管理存储空间
队列：不能实现多对共享；删除数据在表头进行操作；遵循“先进先出”原则；应用场景一般在计算机系统中各种资源的管理，消息缓冲器的管理和广度优先搜索遍历等；栈分为顺序队和链队，其中顺序队如果内存不足需要通过编程手段扩大数组长度，链队相当于顺序表的单链表，只能头进尾出

两者均是一对一逻辑结构，“一对一”的逻辑关系指的是对于其中的结点，有且仅有一个开始结点没有前驱但有一个后继结点，有且仅有一个终端结点没有后继但有一个前驱结点，其它的结点都有且仅有一个前驱和一个后继结点。栈的插入和删除操作只允许在表的尾端进行，队列只允许在表尾插入数据元素，在表头删除数据元素

1.2上述思维导图

2.PTA实验作业

2.1字符串是否对称

2.1.1设计思路

    定义栈s和字符数组ch
    初始化栈s
    输入字符ch
    将所有的字符ch进到栈s
    遍历字符数组ch，如果字符不匹配出栈的字符，说明该字符串不对称
    否则该字符串对称

2.1.2代码截图

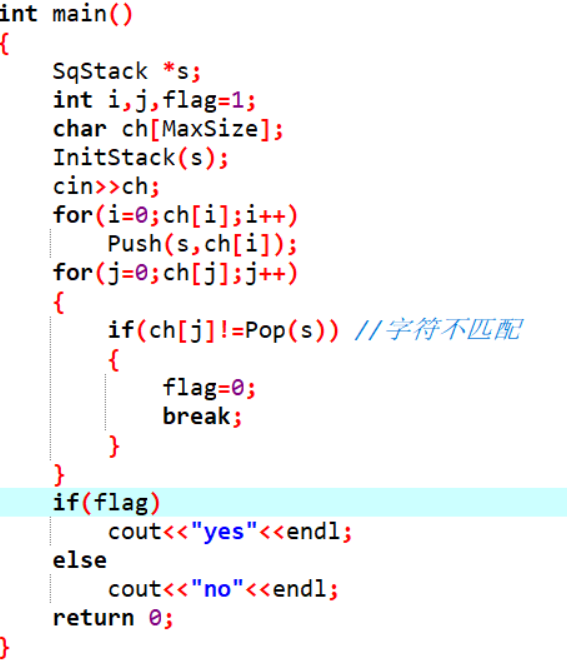
2.1.3PTA提交列表

编译错误主要是部份函数没有声明导致

2.2报数游戏

2.2.1设计思路

int main()
    定义Queue型指针Q
    输入退出编号m和初始人数n
    定义index暂存退出编号m
    初始化Q，将数据进队
    遍历Q
        while数到退出编号m时
            先将Q出队赋值给a
            再将a进队
        输出出队的编号
        令m初始化（m=index）继续遍历直到队空

2.2.2代码截图

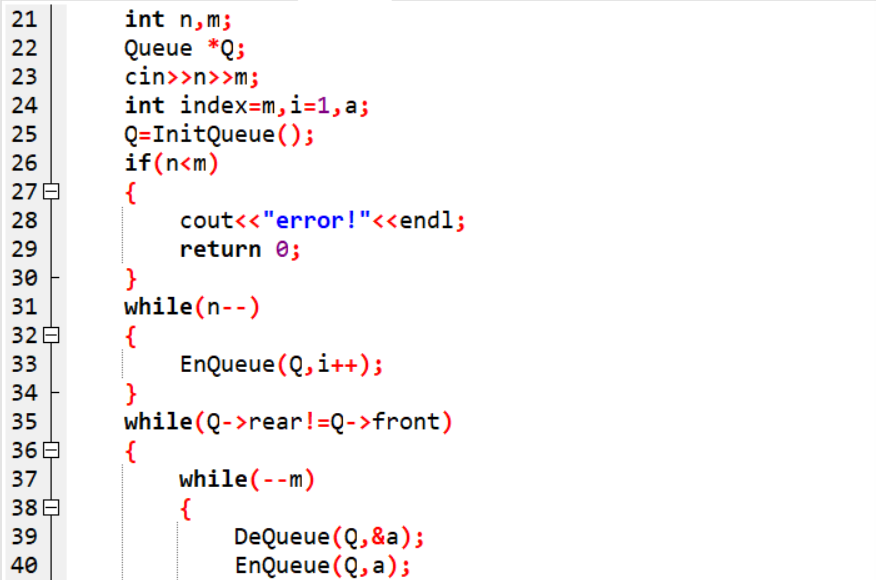
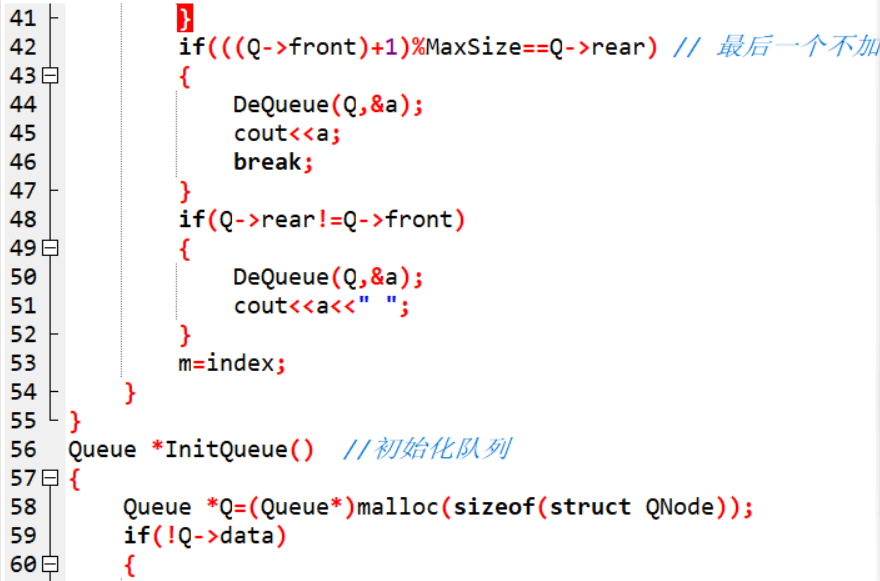
2.2.3PTA提交列表

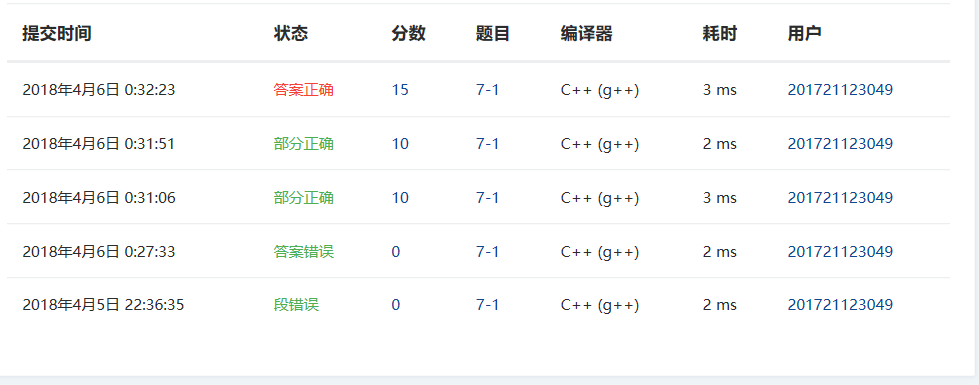
答案错误的原因时出对函数的形参定义错误，将ElemType &e写成了ElemType e，调用函数的同时没有改变e的值

2.3 银行排队问题之单队列多窗口服务

2.3.1设计思路

将顾客信息进队
遍历队列
    按到达时间分配窗口的顾客，依次算出每个顾客的等待时间和窗口的业务处理时间和人数
    如果下一个顾客到达时间大于上一个顾客，计算当前窗口的等待时间，计算最长等待时间和总等待时间
遍历每个窗口，比较算出最晚完成时间
计算输出平均等待时间、最长等待时间和最晚完成时间

2.3.2代码截图

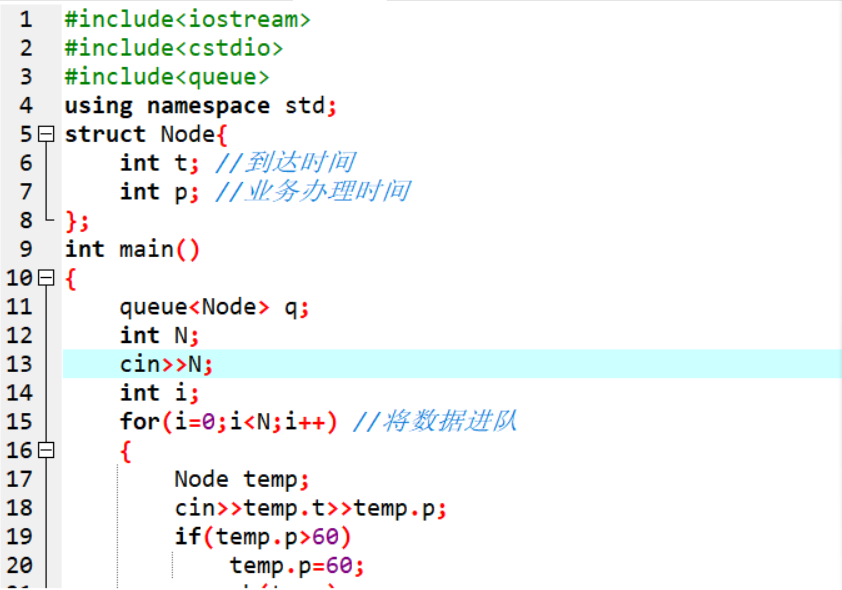
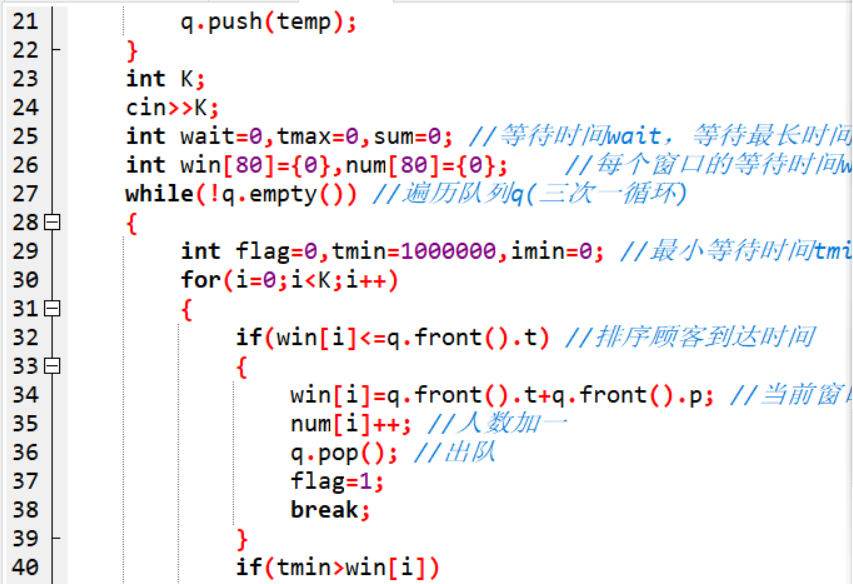
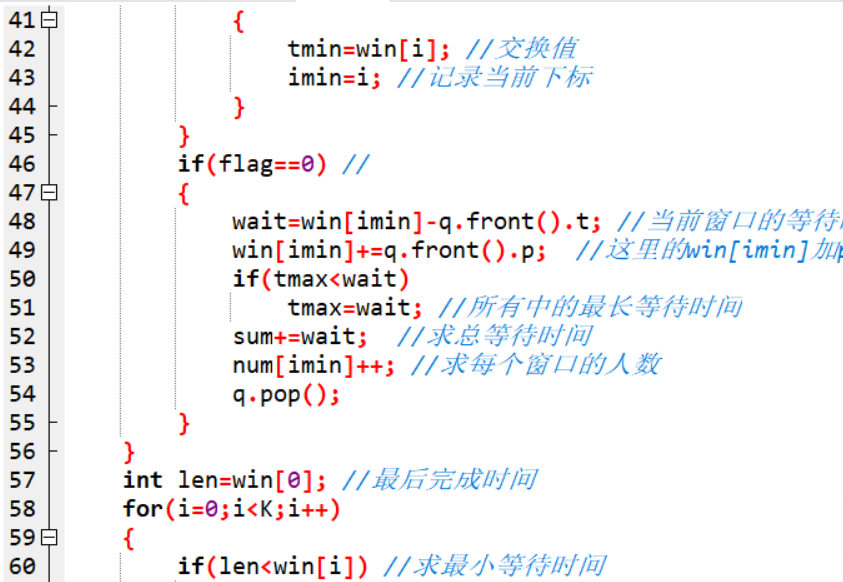
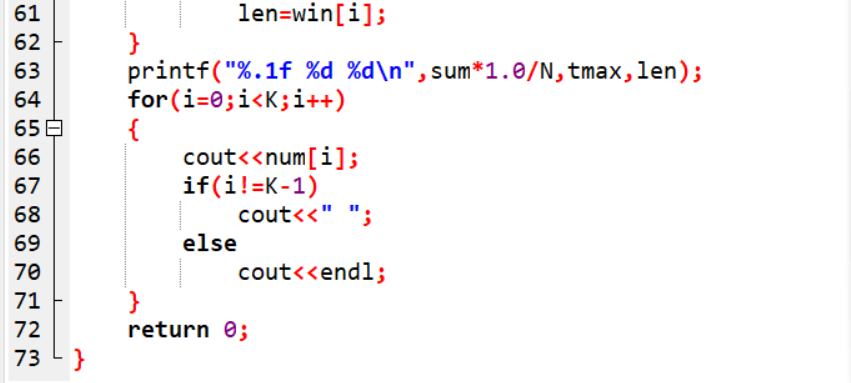
2.3.3PTA提交提交列表

将当前窗口繁忙时间win[imin]+=q.front().p错写成win[imin]+=wait导致win错误，殃及后面等待时间的计算

3截图本周题目及的PTA最后排名

3.1栈PTA排名

3.2队列PTA排名

3.3我的总分

225

4.阅读代码： 堆栈模拟队列

#include <iostream>  
#include <stack>  
#include <string>  
using namespace std;  
  
stack<int> staIn, staOut;  
  
int main()  
{  
    int n1, n2;  
    cin>>n1>>n2;  
    if(n1 > n2)  
        n1 = n2;  
    string s;  
      
    while(cin>>s, s != "T")  
    {  
        if(s == "A")  
        {  
            int t;  
            cin>>t;  
  
            if(staIn.size() == n1)  
            {  
                if(staOut.size() > 0)  
                {  
                    cout<<"ERROR:Full"<<endl;  
                    continue;  
                }  
                int i;  
                for(i = 0; i < n1; ++i)  
                {  
                    staOut.push(staIn.top());  
                    staIn.pop();  
                }  
            }  
  
            if(staIn.size() < n1)  
                staIn.push(t);  
            else  
            {  
                cout<<"ERROR:Full"<<endl;  
                continue;  
            }  
        }  
        else if(s == "D")  
        {  
            if(staOut.size() == 0)  
            {  
                if(staIn.size() == 0)  
                {  
                    cout<<"ERROR:Empty"<<endl;  
                    continue;  
                }  
                int i, size = staIn.size();  
                for(i = 0; i < size; ++i)  
                {  
                    staOut.push(staIn.top());
                    staIn.pop();  
                }  
            }  
            cout<<staOut.top()<<endl;  
            staOut.pop();  
        }  
    }  
    return 0;  
} 

功能：用两个栈实现队列的出队入队操作
优点：他这题巧妙的利用了栈的先进后出原理，将一个栈作为发出栈，负责出栈元素，另一个栈作为接收栈，负责接收元素，发出栈的元素先出栈再入到接受栈后就能逆置元素（staOut.push(staIn.top())，staIn.pop()），从而得到队头元素，实现入队操作；若要执行出队操作的话，同入队操作，出栈之后再入栈，能够实现出队的队头元素放置到栈顶实现出栈
https://blog.csdn.net/a418382926/article/details/21635879

5.代码Git提交列表截图