C++数字三角形问题与dp算法

题目：数字三角形

题目介绍：如图所示的数字三角形，要求从最上方顶点开始一步一步下到最底层，每一步必须下一层，求出所经过的数字的最大和。

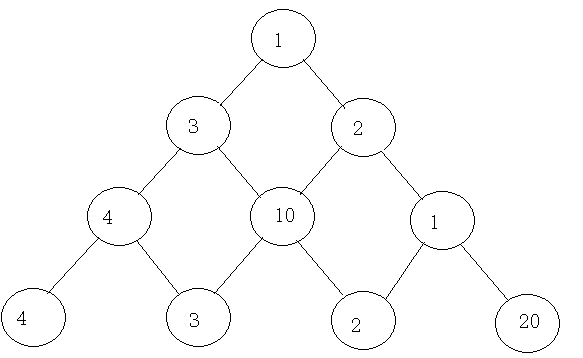
输入：第一行值n，代表n行数值；后面的n行数据代表每一行的数字。

输出：经过数字的最大和。

例：

输入：

4

1

3 2

4 10 1

4 3 2 20

输出：

24

分析：这也是一个典型的贪心算法无法解决的问题，同样可以用动态规划（dp算法）来解决。把边界数字首先初始化到结果矩阵中，再根据状态方程完成结果矩阵的遍历。需要注意的就是数组不是矩形而是三角形，与传统的状态方程相比需要做点改进。

数组编号：

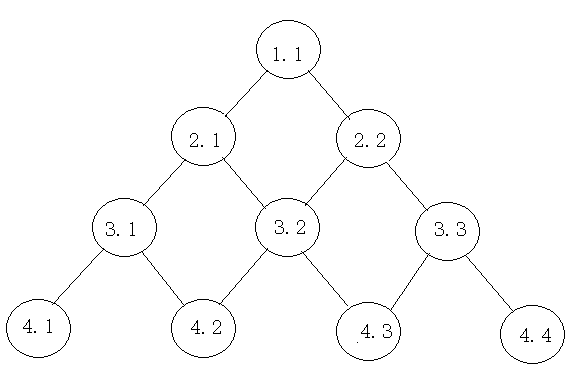
状态方程：p[ i ][ j ]=max{ p[ i-1 ][ j-1 ] , p[ i-1 ][ j ]}

代码如下：

#include <iostream>
using namespace std;
int main()
{
    int i;
    int n;
    cin >> n;
    int **p = new int *[n];
    for (i = 0; i < n; i++)
    {
        p[i] = new int[n];
    }
    for (i = 0; i < n; i++)
    {
        for (int j = 0; j <= i; j++)
        {
            cin >> p[i][j];
        }
    }
    for (i = 1; i < n; i++)
    {
        p[i][0] += p[i - 1][0];
    }
    for (i = 1; i < n; i++)
    {
        p[i][i] += p[i - 1][i - 1];
    }
    for (i = 2; i < n; i++)
    {
        for (int j = 1; j < i; j++)
        {
            p[i][j] += (p[i - 1][j - 1] > p[i - 1][j]) ? p[i - 1][j - 1] : p[i - 1][j];
        }
    }
    for (i = 0; i < n; i++)
    {
        for (int j = 0; j <= i; j++)
        {
            cout << p[i][j] << " ";
        }
        cout << endl;
    }
}

结果如下图：

所以最下层的数字和最大值是24.