Codeforces Round #442 (Div. 2) E Danil and a Part-time Job (dfs序加上一个线段树区间修改查询)

题意：

给出一个具有N个点的树，现在给出两种操作：

1.get x，表示询问以x作为根的子树中，1的个数。

2.pow x，表示将以x作为根的子树全部翻转（0变1,1变0）.

 

思路：dfs序加上一个线段树区间修改查询。

 

AC代码：

#include<iostream>
#include<vector>
#include<string.h>
using namespace std;
const int maxn=2e5+5;
int sum[maxn<<2],lazy[maxn<<2],a[maxn],num[maxn],lft[maxn],rght[maxn],tot;
char s[10];
vector<int>map[maxn];

void build(int k,int l,int r){
    if(l==r){
        sum[k]=a[num[l]];
        return ;
    }
    int mid=(l+r)/2;
    build(k*2,l,mid);
    build(k*2+1,mid+1,r);
    sum[k]=sum[k*2]+sum[k*2+1];
}

void pushdown(int k,int l,int r){
    if(lazy[k]){
        int mid=(l+r)/2;
        sum[k*2]=mid-l+1-sum[k*2];
        sum[k*2+1]=r-mid-sum[k*2+1];
        //sum[k]=sum[k*2]+sum[k*2+1];
        lazy[k*2]^=1;
        lazy[k*2+1]^=1;
        lazy[k]=0;
    }
}

void update(int k,int l,int r,int L,int R){
    if(L<=l&&r<=R){
        sum[k]=r-l+1-sum[k];
        lazy[k]^=1;
        return;
    }
    pushdown(k,l,r);
    int mid=(l+r)/2;
    if(mid>=L)update(k*2,l,mid,L,R);
    if(mid<R)update(k*2+1,mid+1,r,L,R);
    sum[k]=sum[k*2]+sum[k*2+1];
    return ;
}

int query(int k,int l,int r,int L,int R){
    if(L<=l&&r<=R)return sum[k];
    int ans=0;
    pushdown(k,l,r);
    int mid=(l+r)/2;
    if(mid>=L)ans+=query(k*2,l,mid,L,R);
    if(mid<R)ans+=query(k*2+1,mid+1,r,L,R);
    //sum[k]=sum[k*2]+sum[k*2+1];
    return ans;
}
//pushdown和query的pushup可以不要，但是在update中pushdown之后需要pushup
 
void dfs(int k){
    lft[k]=++tot;
    for(int i=0;i<map[k].size();i++){
        dfs(map[k][i]);
    }
    rght[k]=tot;
}
//每个点的left序号就是在线段树中的序号
//每个点对应的left[i]-right[i]+1就是每个点的字节点的个数(加上自己)
 
int main(){
    int n,x;
    while(cin>>n){
        for(int i=1;i<=n;i++)map[i].clear();
        for(int i=2;i<=n;i++){
            cin>>x;
            map[x].push_back(i);
        }
        memset(sum,0,sizeof(sum));
        memset(lazy,0,sizeof(lazy));
        tot=0;
        dfs(1);
        /*for(int i=1;i<=n;i++){
            cout<<lft[i]<<' '<<rght[i]<<endl;
        }*/
        for(int i=1;i<=n;i++){
            cin>>a[i];
        }
        for(int i=1;i<=n;i++){
            num[lft[i]]=i;
            //每个点在线段树中的序号和本身不是一样的
            //注意看build函数
        }
        build(1,1,n);
        int q;
        cin>>q;
        for(int i=0;i<q;i++){
            cin>>s>>x;
            if(s[0]=='p'){
                update(1,1,n,lft[x],rght[x]);
            }
            else cout<<query(1,1,n,lft[x],rght[x])<<endl;
        }
    }
    return 0;
}

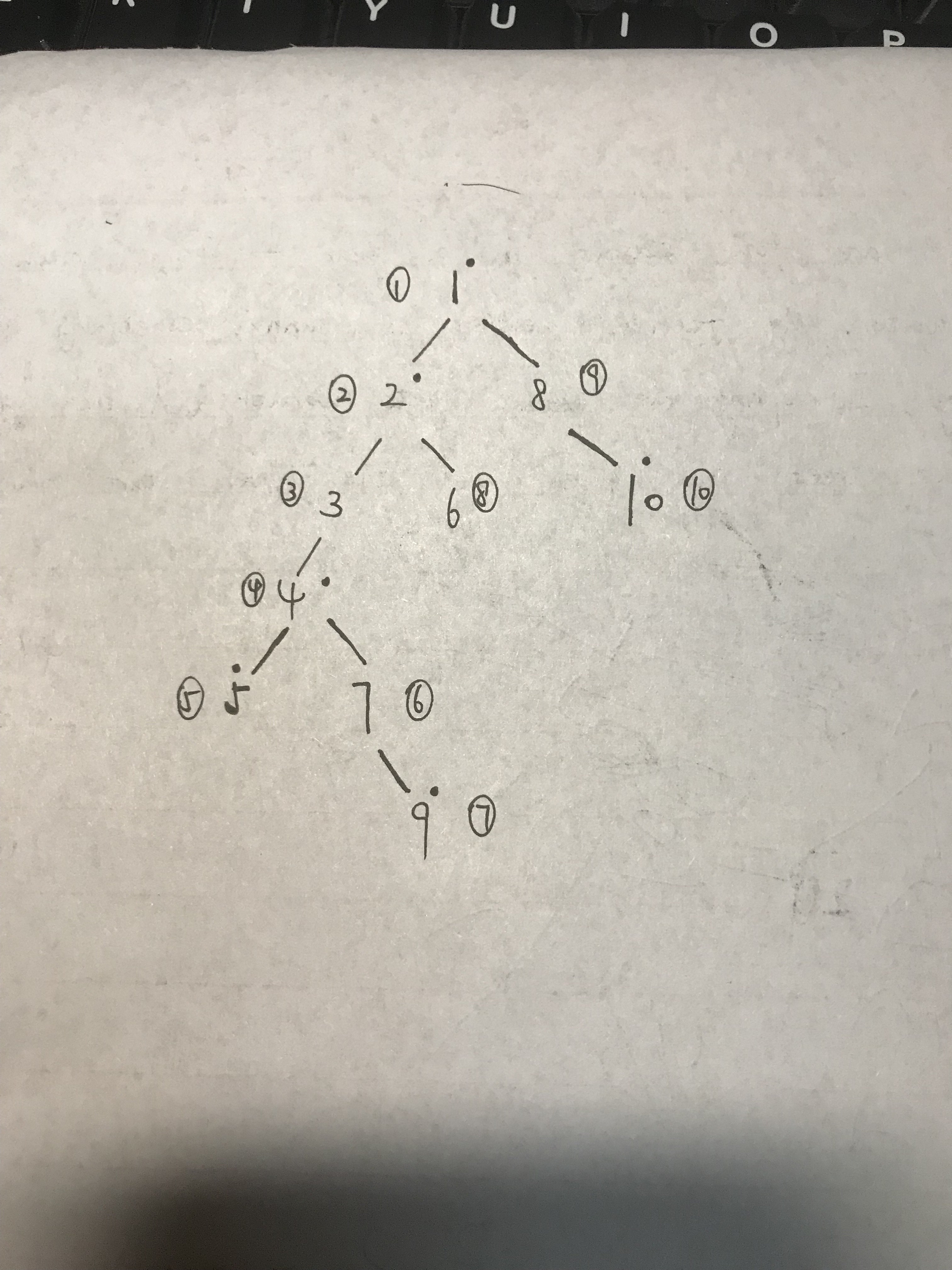
圆圈中的数字是每个节点的left值，每个点的right值就是每个点的子节点中left最大的那个

该图对应输入

10
1 2 3 4 2 4 1 7 8
1 1 0 1 1 0 0 0 1 1
10
pow 1
get 2
pow 2
pow 8
get 6
pow 6
pow 10
get 6
pow 8
pow 3
输出 3 0 1

（第一次看dfs序，看了好久才明白，还耽误了吴老狗睡觉的时间T^T，还是太菜了）