leetcode 5241. 铺瓷砖

题意：

你是一位施工队的工长，根据设计师的要求准备为一套设计风格独特的房子进行室内装修。

房子的客厅大小为 n x m，为保持极简的风格，需要使用尽可能少的 正方形 瓷砖来铺盖地面。

假设正方形瓷砖的规格不限，边长都是整数。

请你帮设计师计算一下，最少需要用到多少块方形瓷砖？

 

示例一：

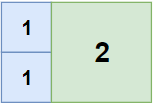
输入：n = 2, m = 3
输出：3
解释：3 块地砖就可以铺满卧室。
     2 块 1x1 地砖
     1 块 2x2 地砖

示例二：

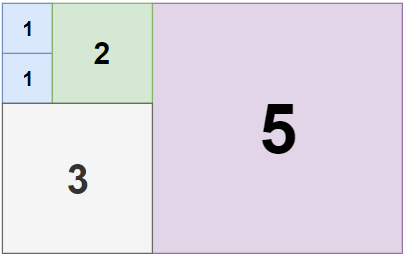
输入：n = 5, m = 8
输出：5

 

示例三：

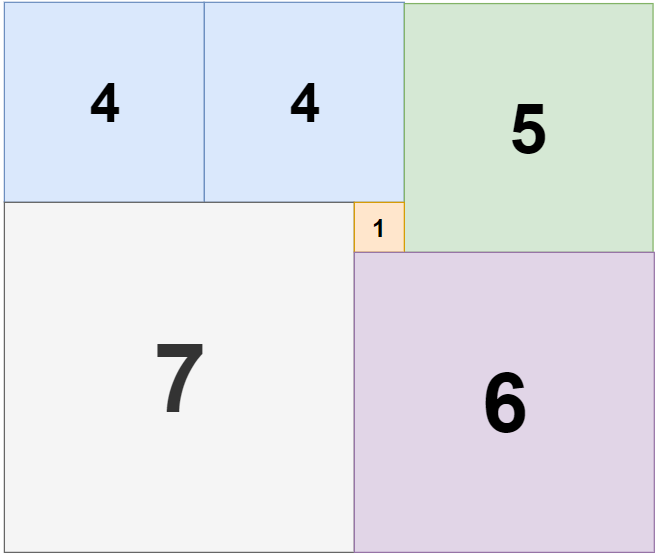
输入：n = 11, m = 13
输出：6

提示：

• 1 <= n <= 13
• 1 <= m <= 13

 

思路：

思路：我们设dp[i][j]：表示组成一个i*j大小的矩形所需要的最小方案数，我们考虑将当前块分三种情况化为更小的块进行求解：

• 1.竖直切一刀 
• 2.水平切一刀 
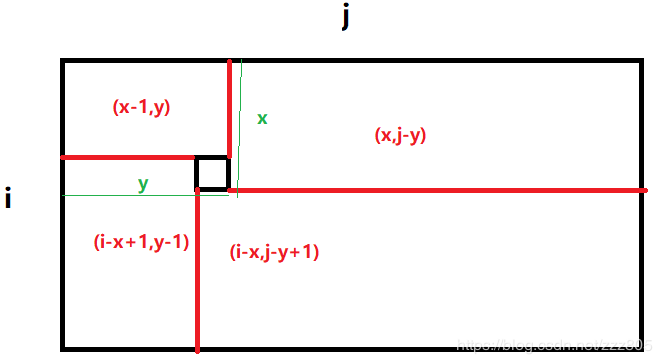
• 3.不规则切割，将一个矩形分成5块，其中中间那块是1*1的

其中前两种情况非常好理解，第三种是为什么呢？ 为什么中间一定是1*1大小的呢？

首先我们知道这道题的n和m很小，只有13这么大，你在草稿纸上画一画就会发现，其实根本不会出现中间出现类似于2*2大小的块使其无法水平或者竖直分割。

class Solution {
public:
    int dp[15][15];
    int tilingRectangle(int n, int m) {
        memset(dp,0x3f,sizeof(dp));
        for(int i=0;i<=m;i++)dp[0][i]=0;
        for(int i=0;i<=n;i++)dp[i][0]=0;
        for(int i=1;i<=n;i++){
            for(int j=1;j<=m;j++){
                if(i==j)dp[i][j]=min(dp[i][j],1);
                for(int k=1;k<j;k++)dp[i][j]=min(dp[i][j],dp[i][k]+dp[i][j-k]);
                for(int k=1;k<i;k++)dp[i][j]=min(dp[i][j],dp[k][j]+dp[i-k][j]);
                for(int p=1;p<=i;p++){
                    for(int q=1;q<=j;q++){
                        dp[i][j]=min(dp[i][j],1+dp[p-1][q]+dp[i-p+1][q-1]+dp[i-p][j-q+1]+dp[p][j-q]);
                    }
                }
            }
        }
        return dp[n][m];
    }
};