leetcode 1074. 元素和为目标值的子矩阵数量
题目
给出矩阵 matrix 和目标值 target,返回元素总和等于目标值的非空子矩阵的数量。
子矩阵 x1, y1, x2, y2 是满足 x1 <= x <= x2 且 y1 <= y <= y2 的所有单元 matrix[x][y] 的集合。
如果 (x1, y1, x2, y2) 和 (x1', y1', x2', y2') 两个子矩阵中部分坐标不同(如:x1 != x1'),那么这两个子矩阵也不同。
示例 1:
输入:matrix = [[0,1,0],[1,1,1],[0,1,0]], target = 0
输出:4
解释:四个只含 0 的 1x1 子矩阵。
示例 2:
输入:matrix = [[1,-1],[-1,1]], target = 0
输出:5
解释:两个 1x2 子矩阵,加上两个 2x1 子矩阵,再加上一个 2x2 子矩阵。
提示:
1 <= matrix.length <= 300
1 <= matrix[0].length <= 300
-1000 <= matrix[i] <= 1000
-10^8 <= target <= 10^8
解题思路
这边matrix.length是300,所以空间复杂度最好控制在O(n^2)。最容易想到的是O(n^4)复杂度的算法。
从以上出发,可以考虑求和的特殊性,把复杂度降低到O(n^3)。
这道题的难点在于二维dp要非常注意顺序,但是如果直接考虑最普遍的矩阵 (x1, y1, x2, y2) 容易不知道从何下手。但是如果从O(n^4)的算法出发,就能发现怎么做简化了。
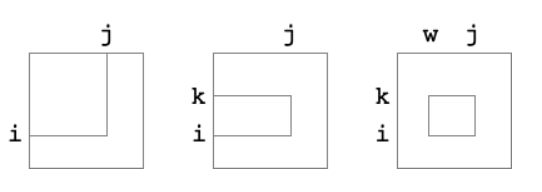
可以看出,矩形可以被分为,用两个参数表示的,用三个参数表示的和用四个参数表示的。三个参数的矩形可以从两个参数的矩形推出(相减),四个参数的矩形可以从三个参数的矩形推出(相减)。如果单纯发现了相减的关系,可以得到O(n^4)的算法。
当我们考虑到四个参数的矩形是由三个参数的矩形得到的时候,可以根据和为sum-target的矩形的个数,去掉对第四个参数的枚举。要得到个数,考虑到和可能很大,所以用unordered_map<int, int>(哈希)。

1 class Solution { 2 public: 3 int dp[310][310]; 4 int numSubmatrixSumTarget(vector<vector<int>>& matrix, int target) { 5 int n=matrix.size(),m=matrix[0].size(); 6 int pre=0; 7 for(int i=0;i<n;i++){ 8 pre=0; 9 for(int j=0;j<m;j++){ 10 pre+=matrix[i][j]; 11 if(i==0)dp[i][j]=pre; 12 else dp[i][j]=dp[i-1][j]+pre; 13 } 14 } 15 int ans=0; 16 for(int i=0;i<n;i++){ 17 for(int j=i;j<n;j++){ 18 unordered_map<int,int>mp; 19 for(int k=0;k<m;k++){ 20 int num=0; 21 if(i==0)num=dp[j][k]; 22 else num=dp[j][k]-dp[i-1][k]; 23 if(num==target)ans++; 24 if(mp.find(num-target)!=mp.end())ans+=mp[num-target]; 25 mp[num]++; 26 } 27 } 28 } 29 return ans; 30 } 31 };
https://blog.csdn.net/qq_37466069/article/details/94172704
https://blog.csdn.net/mathjohn/article/details/92433298




