someting to read before CSP
“不要为明天而忧虑，因为明天自有明天的忧虑；一天的难处一天当就够了。”
念念不忘，必有回响。
考试结束前15分钟停止写代码。然后按照以下顺序进行检查：
-检查文件名是否写错
-检查是否打开文件输入输出
题目名称很重要，值得反复检查。
（太真实咧，xym文件名就打错了，DAY1原地爆炸。不仅如此，他和宏哥两个人 freopen里面的 .in / .out文件名也写错了，都怪JX今年莫名其妙，交上去的源文件名字不是题目名字，而改成了“task1""task2"，简直匪夷所思）
KISS：Keep it simple and stupid
也许上个厕所冷静一下是个好主意！（不过我们考试的时候监考强调：考试结束前三十分钟不能去卫生间了
如果你发现你旁边的人写得很快，放心，他的算法十有八九是错的
走出考场后，除非已经是Day2，永远别对答案
注意数组越界，需不需long long或高精度。
注意删掉无关输出。
注意读入有没有负数。
注意文件操作。（freopen）
尽量少改动代码，还要注意多留备份，以防改正时发现错误而难以撤回。
最后，这是你自己的比赛，不要被他人影响了，也不要去影响他人。
20：2^20=一百万，O(2^n)，搜索
100：100^3=一百万，O(n^3)，Floyd/APSP/搜索
1000：1000^2=一百万，O(n^2)，动态规划/图论
500000：O(nlogn)，二分答案/二分查找/快排/归并
1000000：O(n)或O(1)，数学问题/改变思维方向/贪心
N<=10：O(n!)，全排列算法
N<=12：O(4^n)，状压，如Noip2017的宝藏就有这么做的
N<=18：O(3^n)，状压，如一道叫obelisk的状压dp
N<=20：O(2^n)，状压，应该不会考“是或不是”这种基础搜索法
N<=100：O(n^3)，还可以带一点常数，Floyd或者dp
N<=1000：O(n^2)，dp，图论，
N<=10000：这个范围一般都很玄学⑧。
N<=100000：O(nlog2n)，二分，数据结构，lca等（这个最常见了）
N<=10000000：O(n)，数学方法，贪心 / O(1)，数学方法，贪心，或者不要考虑从N这里下手，或者用上我们的好帮手map。
各数据范围之间可能会串通，灵活考虑。
事实上从空间方面入手也不失为一个好选择，比方说不久前某题N<=6000，dp[6000][6000]开不下，dp[6000][sqrt(6000)]不会做，dp[6000][log(6000)]不会做，dp[6000][2]——做出来了！
先从100分算法思考，如果想不出果断放弃100分，放低要求。
明确算法的正确性后再动手，是正确的还是错误算法骗分，要骗就尽可能骗分。
//部分来自：NOIP考纲总结+NOIP考前经验谈、【原创】Noip考试策略、
以下是我自己在CSP-S考前整理的...
-
1和任何数都互质（除0外）
-
打开guide后，先新建文件并保存为cpp，然后再调整字体大小，并且关掉自动补全单词！注意guide不会自动补全括号！！
-
题目中有输入字符串（即指令）的，用string就很方便
例： string op;cin>>op; if(op=="IR")
-
题目中有提到“第k个插入的数”的，一定要注意下标，运用到函数中有可能是k+1，也有可能是k-1（例：单链表、双链表、
-
处理字符串的时候最好定义len=strlen(s)，修改了s以后strlen(s)会变的！
-
当string中的find()找不到所给字符串的位置时，返回-1（但为了兼容C++各种版本，最好写成string::npos）
-
带有stable的函数可保证相等元素的原本相对次序在排序后保持不变
-
LL指的是long long
-
int：2^31-1（2147483647）>1e9
long long：2^64-1（9223372036854775807）>1e19
-
注意数据范围！能用double就不用float，能用long long就不用int，切记：十年oi一场空，不开ll见祖宗！！！
-
输入中有字符、字符串的时候一定要小心！最好用数组
-
注意题目要求！数组不要老是开那么大，会超时的！！！
-
注意考虑问题的时候别忘了边界处理！
-
最大子段和：预处理前缀和，每次循环最小化要减去的前缀，用数组记录以第i位结尾的最大子段和
-
卡特兰数
-
-
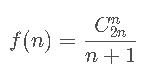
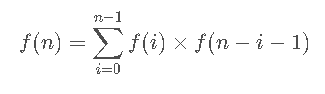
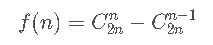
快速幂模板
int ksm(int a,int b,int p) { int res=1; while(b) { if(b&1)res=res*a%p; a=a*a%p; b>>=1; } return res%p; } -
数论（传送门1、传送门2）
-
求欧拉函数值
int phi(int n) { int res=n; for(R i=2;i<=sqrt(n);i++) { if(n%i==0) { res=res/i*(i-1); while(n%i==0)n/=i; } } if(n>1)res=res/n*(n-1);//注意n>1! return res; }线性筛法求φ(1~n)
void work(int n) { for(R i=2;i<=n;i++) { if(!vis[i]) { p[++p[0]]=i; phi[i]=i-1; } for(R j=1;j<=p[0]&&i*p[j]<=n;j++) { vis[p[j]*i]=1; if(i%p[j])phi[i*p[j]]=phi[i]*phi[p[j]]; else { phi[i*p[j]]=p[j]*phi[i]; break; } } } } -
拓展欧几里得
void exgcd(int a,int b,int &g,int &x0,int &y0) { if(b==0) { x0=1;y0=0;g=a; } else { exgcd(b,a%b,g,x0,y0);//不要忘记！！！ int t=x0;x0=y0;y0=t-a/b*y0; } } -
求逆元
一、使用欧拉定理求逆元（a，m互质）
-
二、线性求逆元：递推法
void pre() { inv[1]=1; for(R i=2;i<=n;i++) inv[i]=inv[p%i]*(p-p/i)%p; } -
组合数学
for(R i=0;i<=n;i++) { c[i][0]=1; for(R j=1;j<=i;j++) c[i][j]=c[i-1][j-1]+c[i-1][j]; } -
最长上升子序列 (LIS) 详解+例题模板 (全)
-
最长公共子序列 (LCS) 详解+例题模板（全）
-
DP
-
背包九讲专题
-
闫氏DP分析法，从此再也不怕DP问题！
-
动态规划分为状态表示（集合、属性(max,min,cnt)）和状态计算（不重不漏、划分依据：寻找最后一个不同点）
-
背包问题一般思路：循环物品->体积->决策
-
01背包
for(R i=1;i<=n;i++) for(R j=m;j>=v[i];j--)//倒序 f[j]=max(f[j],f[j-v[i]]+w[i]); -
要求“恰好装满背包”时的最优解
memset(f,-0x3f,sizeof(f));//1023\511\255可变为-1 f[0]=0; -
没有要求必须把背包装满
memset(f,0,sizeof(f)); -
完全背包
for(R i=1;i<=n;i++) for(R j=v[i];j<=m;j++)//正序 f[j]=max(f[j],f[j-v[i]]+w[i]);
/*
01背包：f[i][j]=max(f[i-1][j],f[i-1][j-v]+w);
完全背包：f[i][j]=max(f[i-1][j],f[i][j-v]+w);
*/ -
记住 f[0]=1 啊喂！计数类DP常用完全背包模板（例如：整数划分、货币系统之类的）
for(R i=0;i<=20;i++) for(R j=a[i];j<=n;j++) f[j]=(f[j]+f[j-a[i]])%mod; cout<<f[n]<<endl; -
多重背包
for(R i=1;i<=n;i++) for(R k=1;k<=c[i];k++)//组别在外 for(R j=m;j>=v[i];j--) f[j]=max(f[j],f[j-v[i]]+w[i]); -
分组背包
for(R i=1;i<=n;i++) for(R j=m;j>=0;j--) for(R k=1;k<=c[i];k++)//第i组有c[i]个物品 if(j>=v[i][k])//注意判断 f[j]=max(f[j],f[j-v[i][k]]+w[i][k]); -
背包问题九讲
-
哈希字符串区间和
s[r]-s[l-1]*b[r-l+1]; -
结构体排序别写错了！
bool operator <(const node &x)const -
二分查找模板
while(l<r) int mid=l+r>>1; if(a[mid]>=x) r=mid; else l=mid+1;//查找>=x的最小的数 while(l<r) int mid=(l+r+1)>>1; if(a[mid]<=x) l=mid; else r=mid-1;//查找<=x的最大的数 -
二分答案模板
while(l<=r) l=mid+1; r=mid-1; cout<<r; -
二分精度模板
while(r-l>=eps) if(f(mid)) l=mid; else r=mid; cout<<l; //cout<<r; -
多次循环用register更快
-
求m区间内的最小值（单调队列）
int q[N],h=1,t,n,m,a[N];//有很多细节需要注意，比如这里的h比t大1 int main() { n=read();m=read(); for(R i=1;i<=n;i++) { a[i]=read(); if(h<t&&i-m>q[h]) h++;//这里不需要while，也不需要h<=t printf("%d\n",a[q[h]]); while(a[q[t]]>a[i]&&h<=t) t--;//这里一定要写成h<=t q[++t]=i; } return 0; } -
图论
-
优先队列从小到大
priority_queue<int,vector<int>,greater<int> > q; -
优先队列从大到小（初始即为大根堆）
priority_queue<int,vector<int>,less<int> > q; -
Dijkstra+堆优化
struct edge{ int next,to,w; }e[N]; struct node{ int id,dis; bool operator <(const node &b)const { return dis>b.dis; } }; priority_queue<node> q; void dj(int s) { memset(d,0x3f,sizeof(d)); q.push((node){s,0});d[s]=0; while(!q.empty()) { node now=q.top();q.pop(); int u=now.id; if(v[u])continue; v[u]=1; for(R i=head[u];i;i=e[i].next) { int v=e[i].to; if(d[v]>d[u]+e[i].w) { d[v]=d[u]+e[i].w; q.push((node){v,d[v]}); } } } }
-
Dijkstra 在while内v[i]=1，spfa在插入队列时v[i]=1，没有负环回路就不用spfa，用dijkstra！！！
-
Floyd预处理+循环顺序！（预处理千万别忘了！！！易错
for(R i=1;i<=n;i++) for(R j=1;j<=n;j++) if(i==j)a[i][j]=0; else a[i][j]=inf; for(R p=1;p<=n;p++) for(R i=1;i<=n;i++) if(p!=i) for(R j=1;j<=n;j++) if(p!=j&&i!=j) a[i][j]=min(a[i][j],a[i][p]+a[p][j]); -
多组数据时一定要记得memset
-
求树的重心时还是用动态数组比较好吧
-
模拟栈
stack<int> st; push; empty; top; pop; -
模拟队列
queue<int> q; front;同上 -
DP时别忘了预处理dp数组！区间DP记得memset(dp,0x3f,sizeof(dp))之类的
-
并查集记得预处理fa！
for(int i=1;i<=n;i++)fa[i]=i; -
并查集find函数记得记忆化！
int find(int x) { if(x!=fa[x]) fa[x]=find(fa[x]); return fa[x]; } -
注意别把YES \ Yes \ NO \ No写错了！
-
图论问题输入中有多组数据时，注意在建图前将cnt、h[ ]等清空
-
最小生成树
-
Prim算法 邻接表+堆优化
-
倍增求LCA
void dfs(int u,int fa) { for(R i=head[u];i;i=e[i].nxt) { int v=e[i].to; if(v==fa) continue; f[v][0]=u;d[v]=d[u]+1;//注意d[1]=1 for(R j=1;j<=20;j++) f[v][j]=f[f[v][j-1]][j-1]; dfs(v,u); } } int lca(int x,int y) { if(deep[x]<deep[y])swap(x,y); for(R j=20;j>=0;j--) if(deep[f[x][j]]>=deep[y])//">=" x=f[x][j]; if(x==y)return x; for(R j=20;j>=0;j--) if(f[x][j]!=f[y][j]) { x=f[x][j]; y=f[y][j]; } return f[x][0]; }
