历年真题记录（未完待续

//随便写写

津津的储蓄计划

纯暴力模拟

笨小猴

判断质数、26个字母开26个桶（虽然暴力但问题不大

打表+模拟（会打表真的太重要了

一边输入一边判断

纯暴力模拟（不离散化也没嘚关系

纯暴力模拟（我太菜了只能暴力

string也可以这样子排序！12+34=1234！

神奇的幻方

仔细观察题面，再运用简单的数学思想，不难找出规律（2017年tg初赛T24也考到了幻方

统计数字

STL大法好！map+set（迭代器别忘了set<int>::iterator it ！

均分纸牌

贪心，同时减去平均数，注意一些小细节

砝码称重

动规（注意倒序循环

火柴棒等式

打表+预处理（对数据的估计以及数组的预设！

车站

感觉这种题目都能猜到肯定是要用斐波那契数列的，通过纸上模拟得出系数的规律（不过在智商不够的时候暴力枚举也是一种可行方案呐，运行很快的

无线网络发射器选址

枚举+模拟，主要考察二维矩阵和（用树状数组或者二维前缀和

大水题，直接模拟

一堆字符串处理，没什么好说的

贪心，需要思考一下

同上，if(a[i]>a[i-1])sum+=a[i]-a[i-1];

潜伏者

同样还是考察对字符串的处理

数的划分

递推，本题和某道分苹果的题很相似，都是套路，但是仍有一些剪枝需要小心，不要想得太简单啦！详情见此处

合并果子

用一个小根堆，每次取两次堆顶，再把和加入堆

合并果子加强版

用优先队列的话时间复杂度O(nlogn)，会被1e7的数据卡掉，但其实只要利用x+y的单调性，用两个堆分别维护初始值和插入值，每次取两堆中的最小即可

二分+暴力枚举

深搜+并查集，最后枚举首尾是否相连

处理余数时要小心，注意余数一定是正数丫！

dalao说是结论题叫我不要做了呐，跳过

可以说是非常水的一道题了，会写快速幂就行

模拟+打表，特殊情况要考虑全面

数学思想！！！也许可以这样理解

/*假设两种钱每种最少要拿一次（也就是不能不拿），不能凑成的最小钱数为k，因为a和b互质，显然,k = a * b，(当k = a * b 时，由于ab互质，要么a拿b个，要么b拿a个)。

由于a和b可以一样都不拿，所以ans = k - a - b = a * b - a - b*/

暴搜，仔细理解题面！

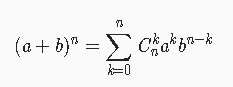
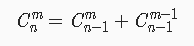
二分答案模板

深搜（寻找公共子串的时候很有趣

在纸上写一写，很明显的贪心

并查集找环（注意更新深度和父节点编号

比较经典的DP，加上高精的话有点难办

搜索+DP真的很强o(￣▽￣)d

DP考虑上一个转移过来的状态，开四维，每一维表示该种卡片使用了多少次，再考虑输入换一种存储方式

金明的预算方案

有依赖的背包问题，其实肥肠容易理解，在第二重循环里面分情况考虑即可（多加几个if，当然这道题只是个例比较好处理

字串变换

BFS+string简直不要太好用！replace(m,sa[i],length(),sb[i])学到咯

货币系统

背包DP+从小到大贪心考虑

加分二叉树

区间DP，注意初始化空树，递归输出前序遍历

 1 #include<bits/stdc++.h>
 2 #define int long long
 3 #define R register int
 4 using namespace std;
 5 int n,root[35][35],f[35][35];
 6 int read()
 7 {
 8     int f=1;char ch;
 9     while((ch=getchar())<'0'||ch>'9')if(ch=='-')f=-1;
10     int res=ch-'0';
11     while((ch=getchar())>='0'&&ch<='9')res=res*10+ch-'0';
12     return res*f;
13 }
14 void print(int l,int r)
15 {
16     if(l>r)return ;
17     if(l==r)
18     {
19         cout<<l<<" ";
20         return ;
21     }
22     cout<<root[l][r]<<" ";
23     print(l,root[l][r]-1);
24     print(root[l][r]+1,r);
25 }
26 signed main()
27 {
28     n=read();
29     for(R i=1;i<=n;i++)f[i][i]=read(),f[i][i-1]=1;
30     //f[n+1][n]=1;
31     for(R i=1;i<=n;i++)
32     {
33         for(R len=2;i+len-1<=n;len++)
34         {
35             int j=i+len-1;
36             for(R k=i;k<=j;k++)
37             {
38                 if(f[i][j]<f[i][k-1]*f[k+1][j]+f[k][k])
39                 {
40                     f[i][j]=f[i][k-1]*f[k+1][j]+f[k][k];
41                     root[i][j]=k;
42                 }
43             }
44         }
45     }
46     cout<<f[1][n]<<endl;
47     print(1,n);
48     return 0;
49 }

View Code

统计单词个数

从后往前进行初始化，string当中substr()和find()的用法

 1 #include<bits/stdc++.h>
 2 #define R register int
 3 using namespace std;
 4 int p,k,len,n,sum[210][210],dp[210][50];
 5 string s,o,a[10];
 6 int read()
 7 {
 8     int f=1;char ch;
 9     while((ch=getchar())<'0'||ch>'9')if(ch=='-')f=-1;
10     int res=ch-'0';
11     while((ch=getchar())>='0'&&ch<='9')res=res*10+ch-'0';
12     return res*f;
13 }
14 bool check(int l,int r)
15 {
16     string tmp=s.substr(l,r-l+1);//tmp为s[l]~s[r]这一段 
17     for(R i=1;i<=n;i++)if(tmp.find(a[i])==0)return true;//若找得到，find()返回a[i]在tmp中的第一个位置 
18     return false;
19 }
20 int main()
21 {
22     p=read();k=read();
23     s+='0';
24     for(R i=1;i<=p;i++)
25     {
26         cin>>o;s+=o;
27     }
28     len=s.length();len--;
29     n=read();
30     for(R i=1;i<=n;i++)cin>>a[i];
31     for(R i=len;i;i--)
32     {
33         for(R j=i;j;j--)
34         {
35             sum[j][i]=sum[j+1][i];
36             if(check(j,i))sum[j][i]++;
37         }
38     }
39     for(R i=1;i<=k;i++)dp[i][i]=dp[i-1][i-1]+sum[i][i];
40     for(R i=1;i<=len;i++)dp[i][1]=sum[1][i];
41     for(R i=1;i<=len;i++)
42     {
43         for(R j=1;j<=k&&j<i;j++)
44         {
45             for(R q=j;q<i;q++)
46             {
47                 dp[i][j]=max(dp[q][j-1]+sum[q+1][i],dp[i][j]);
48             }
49         }
50     }
51     cout<<dp[len][k];
52     
53     return 0;
54 }