状压DP（超详细！！！）

一、定义

总述

状态压缩动态规划，就是我们俗称的状压DP，是利用计算机二进制的性质来描述状态的一种DP方式。

很多棋盘问题都运用到了状压，同时，状压也很经常和BFS及DP连用。

状压dp其实就是将状态压缩成2进制来保存 其特征就是看起来有点像搜索，每个格子的状态只有1或0 ，是另一类非常典型的动态规划

举个例子：有一个大小为n*n的农田，我们可以在任意处种田，现在来描述一下某一行的某种状态：

设n = 9；

有二进制数 100011011（九位），每一位表示该农田是否被占用，1表示用了，0表示没用，这样一种状态就被我们表示出来了：见下表

所以我们最多只需要 2^（n + 1） - 1的十进制数就好（二进制形式是n个1） 现在我们有了表示状态的方法，但心里也会有些不安:上面用十进制表示二进制的数，枚举了全部的状态，DP起来复杂度岂不是很大？没错，状压其实是一种很暴力的算法，因为他需要遍历每个状态，所以将会出现2^n的情况数量，不过这并不代表这种方法不适用：一些题目可以依照题意，排除不合法的方案，使一行的总方案数大大减少从而减少枚举

为了更好的理解状压dp，首先介绍位运算相关的知识。

1. ’&’符号，x&y，会将两个十进制数在二进制下进行与运算(都1为1，其余为0） 然后返回其十进制下的值。例如3(11)&2(10)=2(10)。
2. ’|’符号，x|y，会将两个十进制数在二进制下进行或运算（都0为0，其余为1） 然后返回其十进制下的值。例如3(11)|2(10)=3(11)。
3. ’^’符号，x^y，会将两个十进制数在二进制下进行异或运算（不同为1，其余 为0）然后返回其十进制下的值。例如3(11)^2(10)=1(01)。
4. ’~’符号，~x，按位取反。例如~101=010。
5. ’<<’符号，左移操作，x<<2，将x在二进制下的每一位向左移动两位，最右边用0填充，x<<2相当于让x乘以4。 ’>>’符号，是右移操作，x>>1相当于给x/2，去掉x二进制下的最右一位

1.判断一个数字x二进制下第i位是不是等于1。（最低第1位）

方法：if(((1<<(i−1))&x)>0) 将1左移i-1位，相当于制造了一个只有第i位 上是1，其他位上都是0的二进制数。然后与x做与运算，如果结果>0， 说明x第i位上是1，反之则是0。

2.将一个数字x二进制下第i位更改成1。

方法：x=x|(1<<(i−1)) 证明方法与1类似。

3.将一个数字x二进制下第i位更改成0。

方法：x=x&~(1<<(i−1))

4.把一个数字二进制下最靠右的第一个1去掉。

方法：x=x&(x−1)

二、典型例题

【例题1】骑士(P1896 [SCOI2005]互不侵犯)

题目描述

在 n×n(1<=n<=10) 的棋盘上放 k(0<=k<n×n)个国王，国王可攻击相邻的 8 个格子，求使它们无法互相攻击的方案总数。

输入格式

输入有多组方案，每组数据只有一行，包含两个整数 n 和 k。

输出格式

每组数据一行为方案总数，若不能够放置则输出 0。

输入样例

3 2

4 4

样例输出

16

79

---

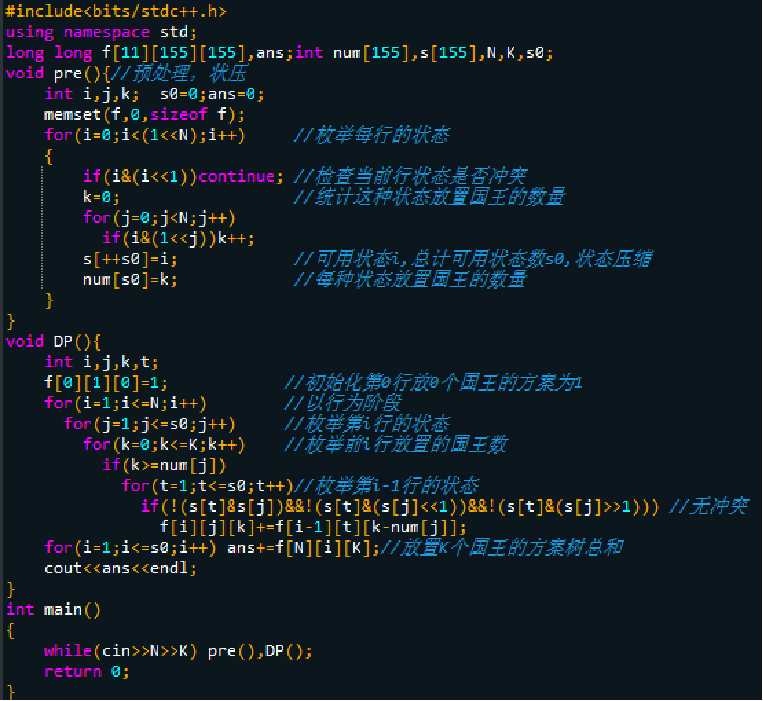
实际状压dp顾名思义，就是采用位运算，来记录更多的必须记录的状态来做dp有了比较深的dp功底后只要对位运算有了解就可以解决问题。。。

考虑到每行每列之间都有互相的约束关系。因此，我们可以用行和列作为另一个状态的部分。用一个新的方法表示行和列的状态：数字。考虑任何一个十进制数都可以转化成一个二进制数，而一行的状态就可以表示成这样——例如：1010(2)

就表示：这一行的第一个格子没有国王，第二个格子放了国王，第三个格子没有放国王，第四个格子放了国王。而这个二进制下的数就可以转化成十进制： 10(10)

于是，我们的三个状态就有了：第几行（用i表示）、此行放什么状态（用j表示）、包括这一行已经使用了的国王数（用s表示）。

考虑状态转移方程。我们预先处理出每一个状态（s[x]）其中包含二进制下1的个数，及此状态下这一行放的国王个数（num[x]），于是就有：

f[i][j][s]=sum(f[i−1][k][s−num[j]])，f[i][j][s]就表示在只考虑前i行时，在前i行（包括第i行）有且仅有s个国王，且第i行国王的情况是编号为j的状态时情况的总数。而k就代表第i-1行的国王情况的状态编号

 

【例题2】牧场的安排(P1879 [USACO06NOV]玉米田Corn Fields)

Farmer John 新买了一块长方形的牧场，这块牧场被划分成 M列 N 行  (1≤M≤12;1≤N≤12)，每一格都是一块正方形的土地。FJ 打算在牧场上的某几格土地里种上美味的草，供他的奶牛们享用。遗憾的是，有些土地相当的贫瘠，不能用来放牧。并且，奶牛们喜欢独占一块草地，于是 FJ 不会选择两块相邻的土地，即：没有哪两块草地有公共边。当然，FJ 还没有决定在哪些土地上种草。 作为一个好奇的农场主，FJ 想知道，如果不考虑草地的总块数，那么，一共有多少种种植方案可供他选择。当然，把新的牧场荒废，不在任何土地上种草，也算一种方案。请你帮 FJ 算一下这个总方案数。

输入格式

第 1行：两个正整数 M 和 N，用空格隔开；第 2到 M+1行：每行包含 N 个用空格隔开的整数，描述了每块土地的状态。输入的第 i+1行描述了第 i行的土地。所有整数均为 0 或 1，1 表示这块土地足够肥沃，0 则表示这块地上不适合种草。

输出格式

第 1 行：输出一个整数，即牧场分配总方案数除以 10^8的余数。

样例输入

2 3

1 1 1

0 1 0

样例输出

9

---

 题目大意

给N*M的棋盘，每个格子不是0就是1,1代表可以种草，否则不能。相邻两个格子不能同时种草，求种草的方案总数。

思路

状态压缩类动态规划，状压dp一般会有明显的数据范围特征，即n,m一般都在20以内。可将每一排的N个看成一个N位二进制，先预处理出每一行可以运行的状态，这样可以去掉很多无效状态（如110），然后DP处理，枚举当前有效状态和上一行有效状态的关系。

f[i][j] 表示第i行在状态j的时候的方案数，其中j我们用一个二进制数来表示。

转移的时候只要判断与当前行和上一行是否冲突即可，如果不冲突，分f[i][j]=∑f[i−1][k]其中k为不冲突的状态。Ans=∑1≤i≤numf[n][i] 就是最后的答案（num为状态总数）。

初始条件：f[1][i]=1 (1<=i<=a[1].num).