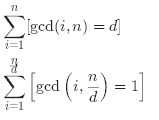[SDOi2012]Longge的问题(洛谷 2303)
题目描述
Longge的数学成绩非常好,并且他非常乐于挑战高难度的数学问题。现在问题来了:给定一个整数N,你需要求出∑gcd(i, N)(1<=i <=N)。
输入格式
一个整数,为N。
输出格式
一个整数,为所求的答案。
输入输出样例
输入 #1
6
输出 #1
15
说明/提示
对于60%的数据,0<N<=2^16
对于100%的数据,0<N<=2^32
本题的重点便在于该如何转化原式∑gcd(i, N),下面我给出变化过程:(时间复杂度: 因子个数*√n
注意,上面的↓↓↓这一步可以说是肥肠常用了!
那么这道题自然就变成了求欧拉函数值的模板题,但同时还有一点优化小技巧,在枚举最大公约数d的时候(代码里写的是i),可以顺便把n/d也一起算。

1 #include<bits/stdc++.h> 2 #define ll long long 3 using namespace std; 4 ll n; 5 ll phi(ll n) 6 { 7 ll ans=n; 8 for(register ll i=2;i*i<=n;i++) 9 if(n%i==0) 10 { 11 ans=ans/i*(i-1); 12 while(n%i==0)n/=i; 13 } 14 if(n>1)ans=ans/n*(n-1); 15 return ans; 16 } 17 ll ff(ll x) 18 { 19 ll res=0LL,i=1LL; 20 for(;i*i<x;i++) 21 if(x%i==0)res+=i*phi(x/i)+(x/i)*phi(i); 22 if(i*i==x)res+=i*phi(i); 23 return res; 24 } 25 int main() 26 { 27 scanf("%lld",&n); 28 printf("%lld",ff(n)); 29 return 0; 30 }