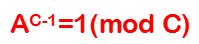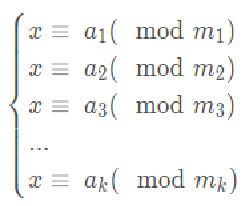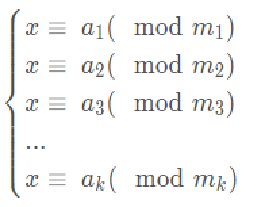同余问题2（超详细！！！）

中国剩余定理

问题:求解同余方程组

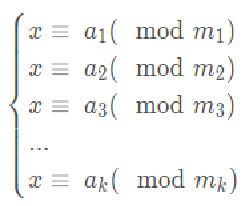
其中m1,m2,m3...mk 为两两互质的整数，求x的最小非负整数解.

 

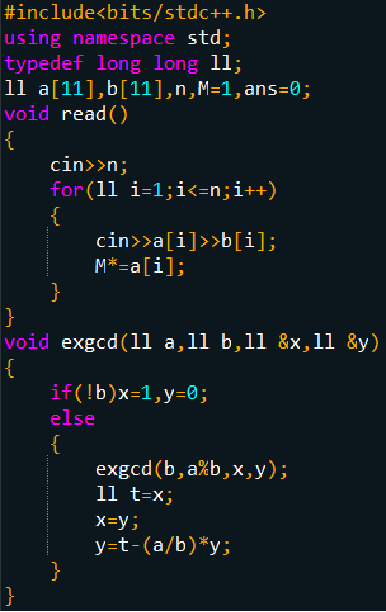
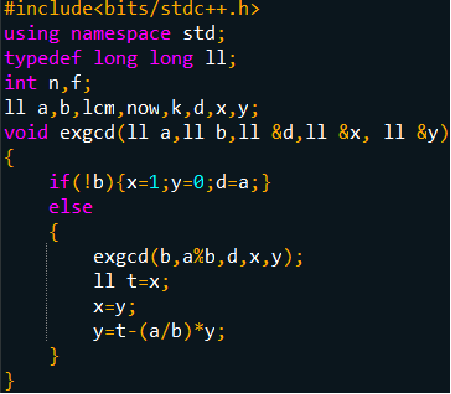
代码：

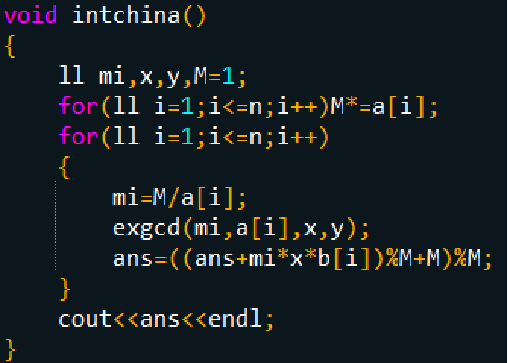
习题：

洛谷 P3868 [TJOI2009]猜数字【中国剩余定理】

例题：

曹冲养猪（信息学奥赛一本通 1634）

【题目描述】

自从曹冲搞定了大象以后，曹操就开始琢磨让儿子干些事业，于是派他到中原养猪场养猪，可是曹冲很不高兴，于是在工作中马马虎虎，有一次曹操想知道母猪的数量，于是曹冲想狠狠耍曹操一把。 举个例子，假如有 16 头母猪，如果建了 3个猪圈，剩下 1 头猪就没有地方安家了；如果建造了 5 个猪圈，但是仍然有 1 头猪没有地方去；如果建造了 7 个猪圈，还有 2 头没有地方去。你作为曹总的私人秘书理所当然要将准确的猪数报给曹总，你该怎么办？

【输入】

第一行包含一个整数 n，表示建立猪圈的次数； 接下来 n 行，每行两个整数 ai,bi，表示建立了 ai个猪圈，有 bi头猪没有去处。你可以假定 ai,aj 互质。

【输出】

输出仅包含一个正整数，即为曹冲至少养猪的数目。

【输入样例】

3 3 1 5 1 7 2

【输出样例】

16

 

---

 扩展中国剩余定理

问题：求解同余方程组

 

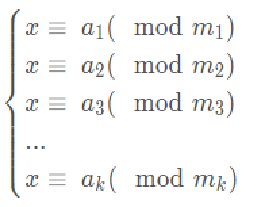
其中m1,m2,m3...mk 为 不一定两两互质的整数，求x的最小非负整数解。

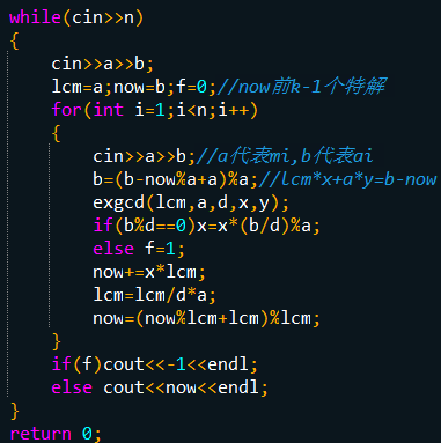
例题：

Strange Way to Express Integers（信息学奥赛一本通 1635）

【题目描述】

给定 2n个正整数 a1,a2,⋯, an和 m1,m2,⋯,mn ，求一个最小的正整数 x，满足 ∀i∈[1,n],x≡ai (mod mi），或者给出无解。

【输入】

多组数据。 每组数据第一行一个整数 n； 接下来 n 行，每行两个整数 mi,ai 。

【输出】

对于每组数据，若无解，输出 −1；否则输出一个非负整数，若有多解，输出最小的满足条件的答案。

【输入样例】

2 8 7 11 9

【输出样例】

31

 

---

 高次同余方程

BSGS（Baby Step Giant Step）算法，又称大小步算法，其主要用于解形如

的高次同余方程中的 x，其核心思想是分块。 当 C为质数时，通过费马小定理：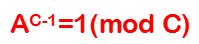

可知，当x>=C-1时，会出现一个循环节，保证答案 x 若存在，必然有x<C-1  

因此，当 C 比较小时，可使用暴力，直接令从 0 枚举到 C-1，检验其是否为方程的解，而当 C 比较大时，使用暴力会 TLE，此时可以采用 BSGS 算法来求解 x，其时间复杂度是sqrt(n) 级别的.

朴素的 BSGS 算法只能处理 C 是质数的情况，扩展的 BSGS 通过同余性质消因子来解决 C 不是质数的情况。

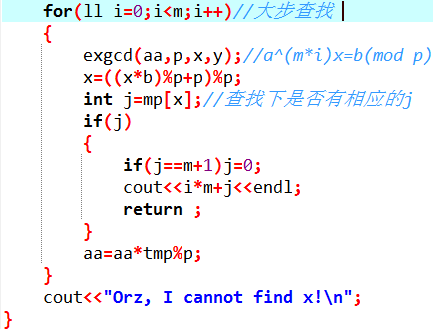
--->关于“map”，不太清楚的话可以参考这里

例题：

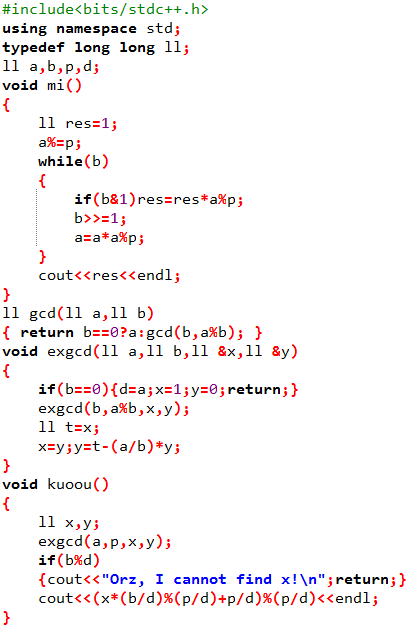
计算器（信息学奥赛一本通 1636）

【题目描述】

你被要求设计一个计算器完成以下三项任务： 1、给定 y,z,p，计算 y^zmod p 的值； 2、给定 y,z,p，计算满足 x×y≡z (mod p)  的最小非负整数 x； 3、给定 y,z,p，计算满足 y^x≡z (mod p )  的最小非负整数 x。

【输入】

输入包含多组数据。 第一行包含两个正整数 T,K分别表示数据组数和询问类型（对于一个测试点内的所有数据，询问类型相同）； 以下 T 行每行包含三个正整数 y,z,p描述一个询问。

【输出】

对于每个询问，输出一行答案。 对于询问类型 2 和 3，如果不存在满足条件的，则输出 Orz, I cannot find x! ，注意逗号与 I 之间有一个空格。

【输入样例】

3 1 2 1 3 2 2 3 2 3 3

【输出样例】

2 1 2

 

我的博客前面还有同余问题1哦