扩散(信息学奥赛一本通 1437)(洛谷 1661)
题目描述
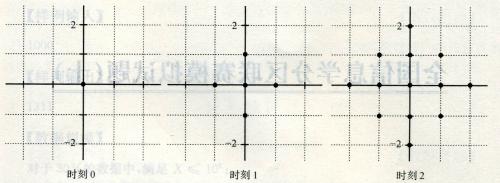
一个点每过一个单位时间就会向四个方向扩散一个距离,如图。
两个点a、b连通,记作e(a,b),当且仅当a、b的扩散区域有公共部分。连通块的定义是块内的任意两个点u、v都必定存在路径e(u,a0),e(a0,a1),…,e(ak,v)。给定平面上的n给点,问最早什么时刻它们形成一个连通块。
输入格式
第一行一个数n,以下n行,每行一个点坐标。
数据规模
对于20%的数据,满足1≤N≤5; 1≤X[i],Y[i]≤50;
对于100%的数据,满足1≤N≤50; 1≤X[i],Y[i]≤10^9。
输出格式
一个数,表示最早的时刻所有点形成连通块。
输入输出样例
输入 #1
2 0 0 5 5
输出 #1
5
事实上,看到题目以后,尽管知道是二分的思路,然鹅我还是不知道该从何下手...(;´ρ`)
后来在网上看到了这位大神的题解,感觉真是豁然开朗,我把两种代码都写了一遍,并分别在ybt和洛谷上提交了,并且全部AC了,感谢大佬提供的思路!
点击即可查看大神思路(真的佩服得五体投地)
floyd+dp
首先我们仔细审一遍题——emm,连通块、任意两点间路径……诶好像有点最短路径的想法!
我们可以这样想,任意两点间的最短距离,由于单位时间内扩散一个单位距离,所以其实也就是两点连通的最短时间的两倍(两点同时扩散)
这里可以用floyd,并不会超时,但是需要注意因为扩散是所有点同时进行的,所以两点之间的距离(d[i][j])推导式要进行一点点变形:
d[i][j]=min(d[i][j],max(d[i][k],d[k][j]));(应该很好理解吧(* ̄︶ ̄))
在进行预处理的时候,任意两点间的距离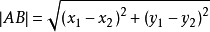
但也可以直接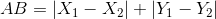
这样在代码中更好运用
最后用两层循环求出图中两点间的 最大的 最短距离 即可,但这还不是答案啦(*๓´╰╯`๓),真正的答案需要再+1、/2,因为这道沙雕题目的设定是——当两点扩散的范围交叉于一点时,是不算“衔接”的,所以还要加上一才行,至于除以二之前已经说过啦

1 #include<bits/stdc++.h> 2 using namespace std; 3 const int N=1e6+5; 4 int x[N],y[N],fa[N],d[100][100]; 5 int n; 6 int m,q,ans,p,tot; 7 int read() 8 { 9 int f=1;char ch; 10 while((ch=getchar())<'0'||ch>'9') 11 if(ch=='-')f=-1; 12 int res=ch-'0'; 13 while((ch=getchar())>='0'&&ch<='9') 14 res=res*10+ch-'0'; 15 return res*f; 16 } 17 void write(int x) 18 { 19 if(x<0) 20 { 21 putchar('-'); 22 x=-x; 23 } 24 if(x>9)write(x/10); 25 putchar(x%10+'0'); 26 } 27 28 29 int main() 30 { 31 n=read(); 32 for(int i=1;i<=n;i++) 33 x[i]=read(),y[i]=read(); 34 for(int i=1;i<n;i++) 35 for(int j=i+1;j<=n;j++) 36 d[i][j]=d[j][i]=abs(x[i]-x[j])+abs(y[i]-y[j]); 37 for(int k=1;k<=n;k++) 38 for(int i=1;i<=n;i++) 39 if(k!=i) 40 for(int j=1;j<=n;j++) 41 if(j!=k&&j!=i) 42 d[i][j]=min(d[i][j],max(d[i][k],d[k][j])); 43 for(int i=1;i<n;i++) 44 for(int j=i+1;j<=n;j++) 45 ans=max(ans,d[i][j]); 46 write((ans+1)/2); 47 return 0; 48 }
并查集+二分
欸看到上面的“两点间的 最大的 最短距离 ” 是不是感jio很熟悉鸭,这就是肥肠典型的二分答案模型啦
所以这道题肯定可以用二分的方法去做,但是关键就在于该用什么来实现我们二分答案的check咧?
之前提到的那位大神就想出了“并查集”的方法(不得不说,真是太妙了)!
每当我们二分出一个mid值时,都用两个循环先判断两点之间距离是否小于两倍的时间,若是就并在同一个集合里。
注意在check函数中要先将每个点的father赋值为自己本身。
判断结束之后就可以再用一次循环遍历每个点,一旦出现有两个点father值都为自己本身(就说明mid不能满足使所有点都在这个时间内连通),就可以直接返回false,将之前二分的 l 变成mid+1,增大时间;
但是如果满足只有一个点的father是其本身的话,那就可以返回true,将二分边界 r 变为mid-1(还得用一个ans变量来存储最后的答案)

1 #include<bits/stdc++.h> 2 using namespace std; 3 const int N=1e6+5; 4 int x[N],y[N],fa[N],d[100][100]; 5 int n; 6 int m,q,w,ans,p,tot; 7 int read() 8 { 9 int f=1;char ch; 10 while((ch=getchar())<'0'||ch>'9') 11 if(ch=='-')f=-1; 12 int res=ch-'0'; 13 while((ch=getchar())>='0'&&ch<='9') 14 res=res*10+ch-'0'; 15 return res*f; 16 } 17 void write(int x) 18 { 19 if(x<0) 20 { 21 putchar('-'); 22 x=-x; 23 } 24 if(x>9)write(x/10); 25 putchar(x%10+'0'); 26 } 27 int find(int x) 28 { 29 if(fa[x]!=x)fa[x]=find(fa[x]); 30 return fa[x]; 31 } 32 bool check(int t) 33 { 34 for(int i=1;i<=n;i++)fa[i]=i; 35 for(int i=1;i<n;i++) 36 for(int j=i+1;j<=n;j++) 37 if(d[i][j]<=t*2) 38 { 39 int fx=find(i),fy=find(j); 40 if(fx!=fy)fa[fy]=fx; 41 } 42 int sum=0; 43 for(int i=1;i<=n;i++) 44 { 45 if(fa[i]==i)sum++; 46 if(sum==2)return false; 47 } 48 return true; 49 } 50 int main() 51 { 52 n=read(); 53 for(int i=1;i<=n;i++) 54 x[i]=read(),y[i]=read(); 55 for(int i=1;i<n;i++) 56 for(int j=i+1;j<=n;j++) 57 d[i][j]=d[j][i]=abs(x[i]-x[j])+abs(y[i]-y[j]); 58 int l=0,r=999999999; 59 while(l<=r) 60 { 61 int mid=l+r>>1; 62 if(check(mid))r=mid-1,ans=mid; 63 else l=mid+1; 64 } 65 write(ans); 66 return 0; 67 }