【题目描述】
学校有n台计算机,为了方便数据传输,现要将它们用数据线连接起来。两台计算机被连接是指它们有数据线连接。由于计算机所处的位置不同,因此不同的两台计算机的连接费用往往是不同的。
当然,如果将任意两台计算机都用数据线连接,费用将是相当庞大的。为了节省费用,我们采用数据的间接传输手段,即一台计算机可以间接的通过若干台计算机(作为中转)来实现与另一台计算机的连接。
现在由你负责连接这些计算机,任务是使任意两台计算机都连通(不管是直接的或间接的)。
【输入】
第一行为整数n(2≤n≤100),表示计算机的数目。此后的n行,每行n个整数。第x+1行y列的整数表示直接连接第x台计算机和第y台计算机的费用。
【输出】
一个整数,表示最小的连接费用。
【输入样例】
3
0 1 2
1 0 1
2 1 0
【输出样例】
2
【提示】
注:表示连接1和2,2和3,费用为2。
1、Prim算法
1 #include<bits/stdc++.h>
2 using namespace std;
3 int g[101][101]; //邻接矩阵
4 int minn[101]; //minn[i]存放蓝点i与白点相连的最小边权
5 bool u[101]; //u[i]=True,表示顶点i还未加入到生成树中
6 int n,i,j;
7 int main()
8 {
9 cin >> n;
10 for (i = 1; i <= n; i++)
11 for (j = 1; j <= n; j++)
12 cin >> g[i][j];
13 memset(minn,0x7f,sizeof(minn)); //初始化为maxint
14 minn[1] = 0;
15 memset(u,1,sizeof(u)); //初始化为True,表示所有顶点为蓝点
16 for (i = 1; i <= n; i++)
17 {
18 int k = 0;
19 for (j = 1; j <= n; j++) //找一个与白点相连的权值最小的蓝点k
20 if (u[j] && (minn[j] < minn[k]))
21 k = j;
22 u[k] = false; //蓝点k加入生成树,标记为白点
23 for (j = 1; j <= n; j++) //修改与k相连的所有蓝点
24 if (u[j] && (g[k][j] < minn[j]))
25 minn[j] = g[k][j];
26 }
27 int total = 0;
28 for (i = 1; i <= n; i++) //累加权值
29 total += minn[i];
30 cout << total << endl;
31 return 0;
32 }
(效率太低, 存储空间太大?)请看下面的↓↓↓
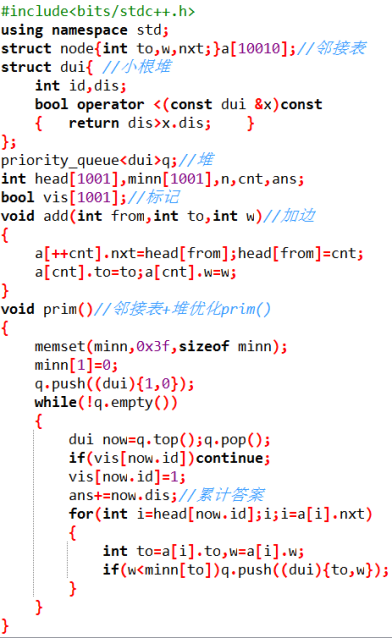
Prim算法 邻接表+堆优化

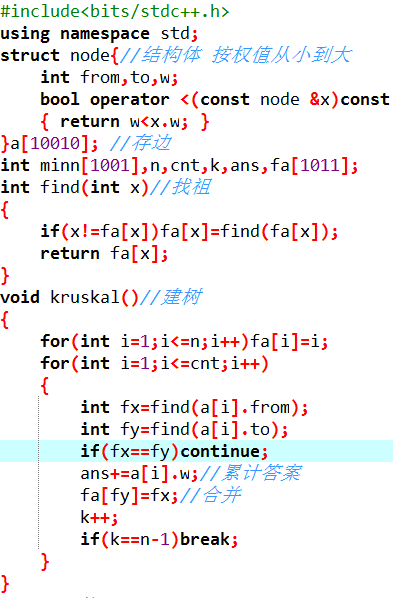
2.Kruskal算法