合并石子（信息学奥赛一本通 1274）

【问题描述】

在一个操场上一排地摆放着Ｎ堆石子。现要将石子有次序地合并成一堆。规定每次只能选相邻的２堆石子合并成新的一堆，并将新的一堆石子数记为该次合并的得分。

【编程任务】

试设计一个程序，计算出将Ｎ堆石子合并成一堆的最小得分。

【输入格式】

第一行为一个正整数N (2≤Ｎ≤100)； 以下Ｎ行,每行一个正整数，小于10000，分别表示第i堆石子的个数(1≤i≤N)。

【输出格式】

为一个正整数，即最小得分。

【输入样例】

7 13 7 8 16 21 4 18

【输出样例】

239

---

【解法一】

以合并的堆数作为阶段

枚举区间起始和终止位置

做出最优决策

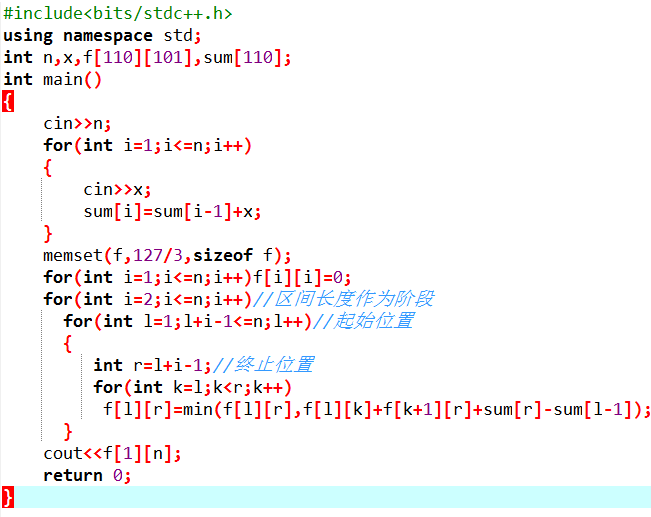
【解法二】

s[i]表示前i堆石头的价值总和，f[i][j]表示把第i堆到第j堆的石头合并成一堆的最优值。

for (i=n-1;i>=1;i--)

for (j=i+1;j<=n;j++)

for (k=i;k<= j-1;k++)

f[i][j]=min(f[i][j],f[i][k]+f[k+1][j]+s[j]-s[i-1]);

输出f[1][n]

#include<cstdio>
#include<cstring>
int f[101][101];
int s[101];
int n,i,j,k,x;
int main()
{
    scanf("%d",&n);
    for (i=1; i<=n; i++) 
    {
        scanf("%d",&x);
        s[i]=s[i-1]+x;
    }
memset(f,127/3,sizeof(f));        //赋值127是很大的正数，若无/3后面的相加
    for (i=1; i<=n; i++) f[i][i]=0;   //可能超出int的范围
    for (i=n-1; i>=1; i--)
        for (j=i+1; j<=n; j++)
            for (k=i; k<=j-1; k++)
                f[i][j]=min(f[i][j],f[i][k]+f[k+1][j]+s[j]-s[i-1]);
    printf("%d\n",f[1][n]);
    return 0;
}