【问题描述】
一个旅行者有一个最多能用m公斤的背包,现在有n件物品,它们的重量分别是W1,W2,...,Wn,它们的价值分别为C1,C2,...,Cn.若每种物品只有一件求旅行者能获得最大总价值。
【输入格式】
第一行:两个整数,M(背包容量,M<=200)和N(物品数量,N<=30); 第2..N+1行:每行二个整数Wi,Ci,表示每个物品的重量和价值。
【输出格式】
仅一行,一个数,表示最大总价值。
【样例输入】package.in
10 4 2 1 3 3 4 5 7 9
【样例输出】package.out
12
f[i][v]=max{ f[i-1][v] , f[i-1][v-w[i]]+c[i] }。
初值f[0][0]=0,其余为负无穷,目标:max{ f [n][j] } 0<=j<=m

(优化空间复杂度)
通过DP的状态转移方程,发现每一阶段i的状态只与上一阶段i-1的状态有关。在这种情况下,我们可以使用称为“滚动数组”的优化方法,降低空间的开销。
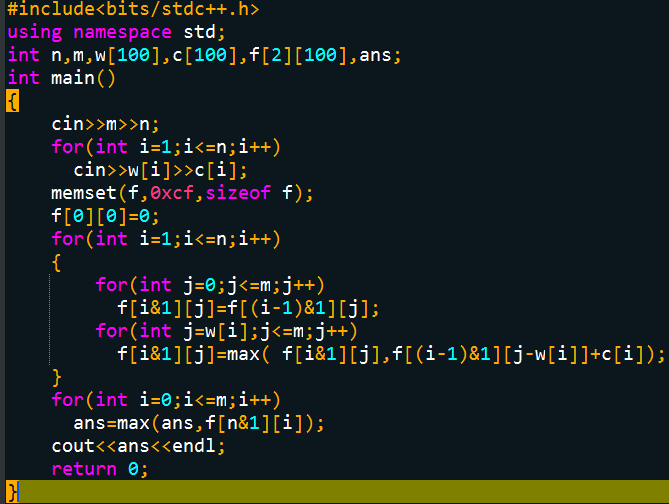
(继续优化空间复杂度)
以上方法的时间和空间复杂度均为O(N*V),其中时间复杂度基本已经不能再优化了,但空间复杂度却可以优化到O(V)。
先考虑上面讲的基本思路如何实现,肯定是有一个主循环i=1..N,每次算出来二维数组f[i][0..V]的所有值。那么,如果只用一个数组f [0..V],能不能保证第i次循环结束后f[v]中表示的就是我们定义的状态f[i][v]呢?f[i][v]是由f[i-1][v]和f[i-1][v-w[i]]两个子问题递推而来,能否保证在推f[i][v]时(也即在第i次主循环中推f[v]时)能够得到f[i-1][v]和f[i-1][v-w[i]]的值呢?事实上,这要求在每次主循环中我们以v=V..0的逆序推f[v],这样才能保证推f[v]时f[v-w[i]]保存的是状态f[i-1][v-w[i]]的值。
伪代码如下:
for i=1..N
for v=V..0
f[v]=max{f[v],f[v-w[i]]+c[i]};
其中f[v]=max{f[v],f[v-w[i]]+c[i]}相当于转移方程f[i][v]=max{f[i-1][v],f[i-1][v-w[i]]+c[i]},因为现在的f[v-w[i]]就相当于原来的f[i-1][v-w[i]]。如果将v的循环顺序从上面的逆序改成顺序的话,那么则成了f[i][v]由f[i][v-w[i]]推知,与本题意不符,但它却是另一个重要的完全背包问题最简捷的解决方案,故学习只用一维数组解01背包问题是十分必要的。
【解法一】
设f[i][v]表示前i件物品,总重量不超过v的最优价值,则f[i][v]=max(f[i-1][v-w[i]]+c[i],f[i-1][v]) ;f[n][m]即为最优解
给出程序:
1 #include<cstdio>
2 using namespace std;
3 const int maxm = 201, maxn = 31;
4 int m, n;
5 int w[maxn], c[maxn];
6 int f[maxn][maxm];
7
8 int max(int x,int y) { x>y?x:y;} //求x和y最大值
9
10 int main(){
11 scanf("%d%d",&m, &n); //背包容量m和物品数量n
12 for (int i = 1; i <= n; i++) //在初始化循环变量部分,定义一个变量并初始化
13 scanf("%d%d",&w[i],&c[i]); //每个物品的重量和价值
14 for (int i = 1; i <= n; i++) // f[i][v]表示前i件物品,总重量不超过v的最优价值
15 for (int v = m; v > 0; v--)
16 if (w[i] <= v) f[i][v] = max(f[i-1][v],f[i-1][v-w[i]]+c[i]);
17 else f[i][v] = f[i-1][v];
18 printf("%d",f[n][m]); // f[n][m]为最优解
19 return 0;
20 }
使用二维数组存储各子问题时方便,但当maxm较大时,如maxm=2000时不能定义二维数组f,怎么办,其实可以用一维数组。
【解法二】
本问题的数学模型如下:设 f[v]表示重量不超过v公斤的最大价值, 则f[v]=max{f[v],f[v-w[i]]+c[i]} ,当v>=w[i],1<=i<=n 。
程序如下:
1 #include<cstdio>
2 using namespace std;
3
4 const int maxm = 2001, maxn = 31;
5 int m, n;
6 int w[maxn], c[maxn];
7 int f[maxm];
8 int main(){
9 scanf("%d%d",&m, &n); //背包容量m和物品数量n
10 for (int i=1; i <= n; i++)
11 scanf("%d%d",&w[i],&c[i]); //每个物品的重量和价值
12
13 for (int i=1; i <= n; i++) //设f(v)表示重量不超过v公斤的最大价值
14 for (int v = m; v >= w[i]; v--)
15 if (f[v-w[i]]+c[i]>f[v])
16 f[v] = f[v-w[i]]+c[i];
17 printf("%d",f[m]); // f(m)为最优解
18 return 0;
19 }
总结
01背包问题是最基本的背包问题,它包含了背包问题中设计状态、方程的最基本思想,另外,别的类型的背包问题往往也可以转换成01背包问题求解。故一定要仔细体会上面基本思路的得出方法,状态转移方程的意义,以及最后怎样优化的空间复杂度。
这个博客讲得超好的呢!




