假设有棵树,长下面这个样子,
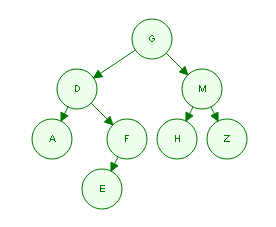
它的前序遍历,中序遍历,后续遍历都很容易知道。
PreOrder: GDAFEMHZ
InOrder: ADEFGHMZ
PostOrder: AEFDHZMG
现在,假设仅仅知道前序和中序遍历,如何求后序遍历呢?
比如,已知一棵树的前序遍历是”GDAFEMHZ”,而中序遍历是”ADEFGHMZ”应该如何求后续遍历?
-
第一步,root最简单,前序遍历的第一节点G就是root。
-
第二步,继续观察前序遍历GDAFEMHZ,除了知道G是root,剩下的节点必然是root的左右子树之外,没法找到更多信息了。
-
第三步,那就观察中序遍历ADEFGHMZ。其中root节点G左侧的ADEF必然是root的左子树,G右侧的HMZ必然是root的右子树。
-
第四步,观察左子树ADEF,左子树的中的根节点必然是大树的root的leftchild。在前序遍历中,大树的root的leftchild位于root之后,所以左子树的根节点为D。
-
第五步,同样的道理,root的右子树节点HMZ中的根节点也可以通过前序遍历求得。在前序遍历中,一定是先把root和root的所有左子树节点遍历完之后才会遍历右子树,并且遍历的右子树的第一个节点就是右子树的根节点。 如何知道哪里是前序遍历中的左子树和右子树的分界线呢?通过中序遍历去数节点的个数。 在上一次中序遍历中,root左侧是A、D、E、F,所以有4个节点位于root左侧。那么在前序遍历中,必然是第1个是G,第2到第5个由A、D、E、F过程,第6个就是root的右子树的根节点了,是M。
-
第六步,观察发现,上面的过程是递归的。先找到当前树的根节点,然后划分为左子树,右子树,然后进入左子树重复上面的过程,然后进入右子树重复上面的过程。最后就可以还原一棵树了。
-
第七步,其实,如果仅仅要求写后续遍历,甚至不要专门占用空间保存还原后的树。只需要稍微改动第六步,就能实现要求。仅需要把第六步的递归的过程改动为如下:
-
确定根,确定左子树,确定右子树。
-
在左子树中递归。
-
在右子树中递归。
-
打印当前根。
2010 求后序遍历
题目描述
输入一棵二叉树的先序和中序遍历序列,输出其后序遍历序列。
输入描述
共两行,第一行一个字符串,表示树的先序遍历,第二行一个字符串,表示树的中序遍历。
输出描述
仅一行,表示树的后序遍历序列。
样例输入
abdehicfg
dbheiafcg
样例输出
dhiebfgca
数据范围及提示
输入长度不大于255。
(信息学奥赛一本通 1339)☟☟☟

-
一、解答本题首先搞清几个概念: 中序遍历:左子树先序遍历+根+右子树先序遍历 先序遍历:根+左子树中序遍历+右子树中序遍历 后序遍历:左子树后序遍历+右子树后序遍历+根 即先、左、右是根据根的遍历顺序命名的
-
二、1、先序遍历的第一个是根,在中序遍历中找到这个根,则中序遍历中根的左边是左子树,右边是右子树
-
2、先序遍历中,若当前位置的节点还有孩子,则当前位置的下一个位置,是以当前位置为根的树的左子树的根。例:先序遍历中a的下一个是b,且a还有孩子,那么a的左子树的根节点是b。所以先序遍历中左子树的第一个节点的位置就是当前位置的下一个。 根据根在中序遍历中的位置,可以确定先序遍历中左子树的最后一个节点的位置。例:先序遍历一部分为abde,中序遍历一部分为dbea,根据前面说的,当前位置是a,以a为根的左子树的根是b,中序遍历中当前范围a左边的节点都是a的左子树,一共有4-1=3个,a在先序遍历中是第1个,所以先序遍历中以a为根节点的左子树的范围的最后一个为1+3=4。
-
3、按照上述方法递归右子树,后序遍历最后输出根
#include<bits/stdc++.h>
using namespace std;
string a,b;
void f(int l1,int r1,int l2,int r2)//当前范围在先序遍历中为[l1,r1],在中序遍历中为[l2,r2]
{
int m=b.find(a[l1]);//在中序遍历中找到根的位置
if(m>l2)f(l1+1,l1+m-l2,l2,m-1);
if(m<r2)f(l1+m-l2+1,r1,m+1,r2);//if判断m不是单独的一个根
cout<<a[l1];
}
int main()
{
cin>>a>>b;//a为先序遍历,b为中序遍历
f(0,a.length()-1,0,b.length()-1);
return 0;
}
//参考:codevs2010 求后序遍历 - TRTTG - 博客园 https://www.cnblogs.com/TheRoadToTheGold/p/6159013.html
已知二叉树的中序遍历和前序遍历,如何求后序遍历 - 可我只是梦呓,半生半生的无力 - CSDN博客 https://blog.csdn.net/qq_29538137/article/details/78447691




