深入研究不平衡回归问题
深入研究不平衡回归问题
- 针对深度不平衡回归这一问题,提出了两种方法:
- 标签分布平滑
- 特征分布平滑
- 传统的解决方案
- 基于数据的解决方案
- 对少数样本过采样、对多数样本欠采样
- 基于模型的解决方案
- 对损失函数的重加权
- 一些学习技巧: transfer learning,meta-learning, two-stage training
- 基于数据的解决方案
-
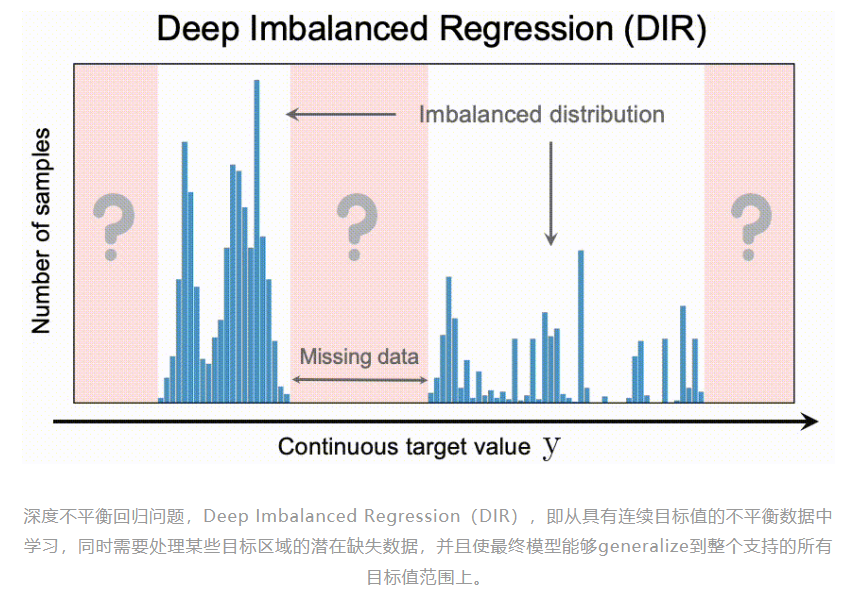
难点与挑战
-
给定连续的,并且可能无穷多的目标值,类与类之间的hard boundaries不再存在。那么当直接应用传统的不平衡分类方法,例如重采样或重加权,因其是对于特定的离散的类别进行操作,这就导致了这些方法不直接适用于连续域的情况。
-
连续标签本质上在不同目标值之间的距离是具有意义,不同的不平衡分布意义不一样。
-
某些目标值可能就根本没有数据。而这也激发了对目标值做 extrapolation 以及 interpolation 的需求。
-
-
标签分布平滑
测试误差的分布与标签密度的分布非常相关
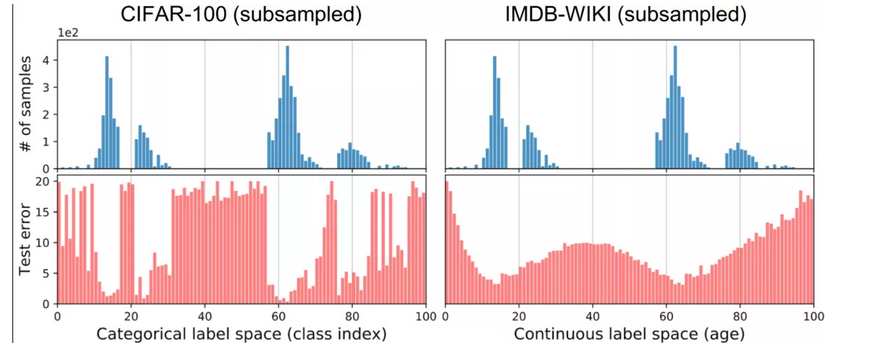
有趣的是,即使标签密度分布与CIFAR-100相同,具有连续的标签空间的 IMDB-WIKI的测试误差分布也与CIFAR-100非常不同。尤其是,IMDB-WIKI的误差分布更加平滑,并且不再与标签密度分布很好地相关,这里的 Pearson correlation 只有 −0.47。
这种现象表明,对于连续标签,其经验标签密度(empirical label density),也就是直接观测到的标签密度,不能准确反映模型或神经网络所看到的不平衡。因此,在连续的情况下,empirical label density是不能反映实际的标签密度分布。这是由于相临近标签(例如,年龄接近的图像)的数据样本之间是具有相关性,或是互相依赖。
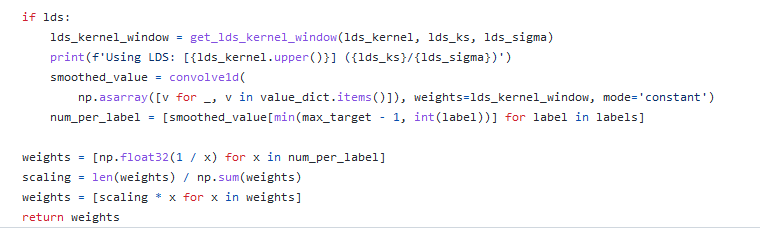
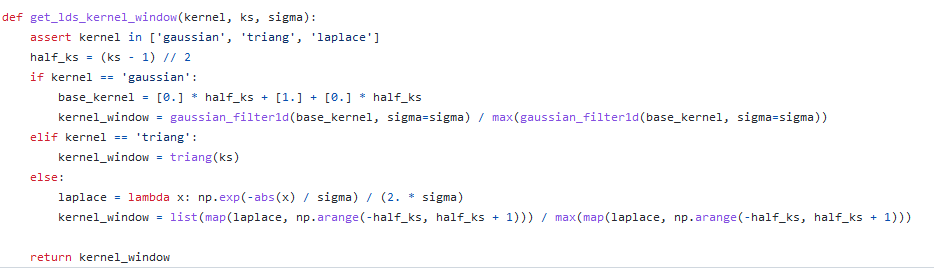
标签分布平滑:基于这个观察,提出 Label Distribution Smoothing (LDS) ,来估计在连续标签情况下的有效label density distribution。方法参考了在统计学习领域中的核密度估计,kernel density estimation的思路,来在这种情况下估计expected density。具体而言,给定连续的经验标签密度分布,LDS 使用了一个 symmetric kernel distribution 对称核函数,用经验密度分布与之进行卷积,来拿到一个 kernel-smoothed的版本,我们称之为 effective label density,也就是有效的标签密度,用来直观体现临近标签的数据样本具有的信息重叠的问题。那么我们也可以进一步验证,由LDS计算出的有效标签密度分布结果现已与误差分布良好相关,皮尔森相关系数为 −0.83。这表明了利用 LDS,我们能获得实际影响回归问题的不平衡的标签分布。
那么有了用LDS估计出的有效标签密度,之前用来解决类别不平衡问题的方法,便可以直接应用于DIR。比如说,一种直接的可以adapted 的方法是利用重加权方法,具体来说就是,我们通过将损失函数乘以每个目标值的LDS估计标签密度的倒数来对其进行加权。之后在实验部分我们也会展示,利用LDS可以一致提升很多方法。
- 参考思想:核密度估计
https://blog.csdn.net/unixtch/article/details/78556499
思路:用对称核函数卷积标签,用于体现有效标签密度分布结果与误差分布的相关性。(核心是用对称核函数卷积连续分布的经验标签)可以将损失函数乘以每个目标值的LDS估计标签密度的倒数来对其进行加权。

-
特征分布平滑

FDS对特征空间进行分布的平滑,本质上是在临近的区间之间传递特征的统计信息。此过程主要作用是去校准特征分布的潜在偏差估计,尤其是对那些样本很少的目标值而言。
方法:
- whitening and re-coloring 白化变换(FDS.py)
- 网络末尾增加校准层来集成FDS (resnet.py)
- 在每个epoch 采用了对于 running statistics的 momentum update,也就是动量更新(FDS.py)





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
· 单元测试从入门到精通
· 上周热点回顾(3.3-3.9)
· winform 绘制太阳,地球,月球 运作规律