动手学习pytorch——（1）线性回归

　　最近参加了伯禹教育的动手学习深度学习项目，现在对第一章（线性回归）部分进行一个总结。

这里从线性回归模型之从零开始的实现和使用pytorch的简洁两个部分进行总结。

　　损失函数，选取平方函数来评估误差，公式如下：

 

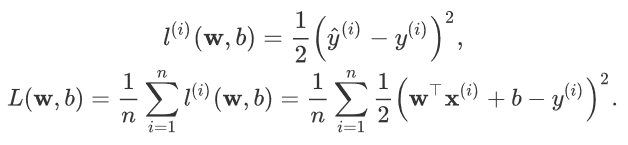
1）从零开始实现

　　　　首先设置真实的权重和偏差w，b。随机生成一个二维数组并由此生成对应的真实labels。

num_inputs = 2   #二个自变量
num_examples = 1000

# set true weight and bias in order to generate corresponded label
true_w = [2, -3.4]
true_b = 4.2

features = torch.randn(num_examples, num_inputs, dtype=torch.float32)
#1000*2

labels = true_w[0] * features[:, 0] + true_w[1] * features[:, 1] + true_b

labels += torch.tensor(np.random.normal(0, 0.01, size=labels.size()),
                       dtype=torch.float32)
#加上一点正态分布的噪声

　　　　对于回归问题的数据，可以先用TensorData进行封装，然后再用DataLoader读取。

　　　　初始化模型参数，这里用下图的代码进行初始化。其实在pytorch中可以用torch.nn.init.normal_(tensor, a=0, b=1)等方法进行初始化。

w = torch.tensor(np.random.normal(0,0.01(num_inputs,1)),dtype=torch.float32)
b = torch.zeros(1, dtype=torch.float32)

w.requires_grad_(requires_grad=True)
b.requires_grad_(requires_grad=True)

 　　　　接着定义模型、损失函数和优化函数。

def linreg(X, w, b):
    return torch.mm(X, w) + b

def squared_loss(y_hat, y): 
    return (y_hat - y.view(y_hat.size())) ** 2 / 2

def sgd(params, lr, batch_size): 
    for param in params:
        param.data -= lr * param.grad / batch_size    #参数更新，这里用param.data，手动更新而不使用梯度来自动更新

 　　　　最后训练，如下：

lr = 0.03   #设置学习率和epoch
num_epochs = 5

net = linreg
loss = squared_loss

for epoch in range(num_epochs):  # training repeats num_epochs times
    # in each epoch, all the samples in dataset will be used once
    # X is the feature and y is the label of a batch sample
    for X, y in data_iter(batch_size, features, labels):
        l = loss(net(X, w, b), y).sum()  
        # calculate the gradient of batch sample loss 
        l.backward()  
        # using small batch random gradient descent to iter model parameters
        sgd([w, b], lr, batch_size)  
        # reset parameter gradient
        w.grad.data.zero_()
        b.grad.data.zero_()
    train_l = loss(net(features, w, b), labels)
    print('epoch %d, loss %f' % (epoch + 1, train_l.mean().item()))

2）pytorch简洁实现

import torch.utils.data as Data
import torch.optim as optim

batch_size = 10

# combine featues and labels of dataset
dataset = Data.TensorDataset(features, labels)

# put dataset into DataLoader
data_iter = Data.DataLoader(
    dataset=dataset,            # torch TensorDataset format
    batch_size=batch_size,      # mini batch size
    shuffle=True,               # whether shuffle the data or not
    num_workers=2,              # read data in multithreading
)

class LinearNet(nn.Module):
    def __init__(self, n_feature):
        super(LinearNet, self).__init__()      # call father function to init 
        self.linear = nn.Linear(n_feature, 1)  # function prototype: `torch.nn.Linear(in_features, out_features, bias=True)`

    def forward(self, x):
        y = self.linear(x)
        return y
    
net = LinearNet(num_inputs)

init.normal_(net[0].weight, mean=0.0, std=0.01)  #参数初始化
init.constant_(net[0].bias, val=0.0)  

loss = nn.MSELoss()
optimizer = optim.SGD(net.parameters(), lr=0.03)   # built-in random gradient descent function

num_epochs = 3
for epoch in range(1, num_epochs + 1):
    for X, y in data_iter:
        output = net(X)
        l = loss(output, y.view(-1, 1))  #count loss
        optimizer.zero_grad() # reset gradient, equal to net.zero_grad()
        l.backward()     # backpropogation
        optimizer.step()  # gradient optimizing
    print('epoch %d, loss: %f' % (epoch, l.item()))

# result comparision
dense = net[0]
print(true_w, dense.weight.data)
print(true_b, dense.bias.data)