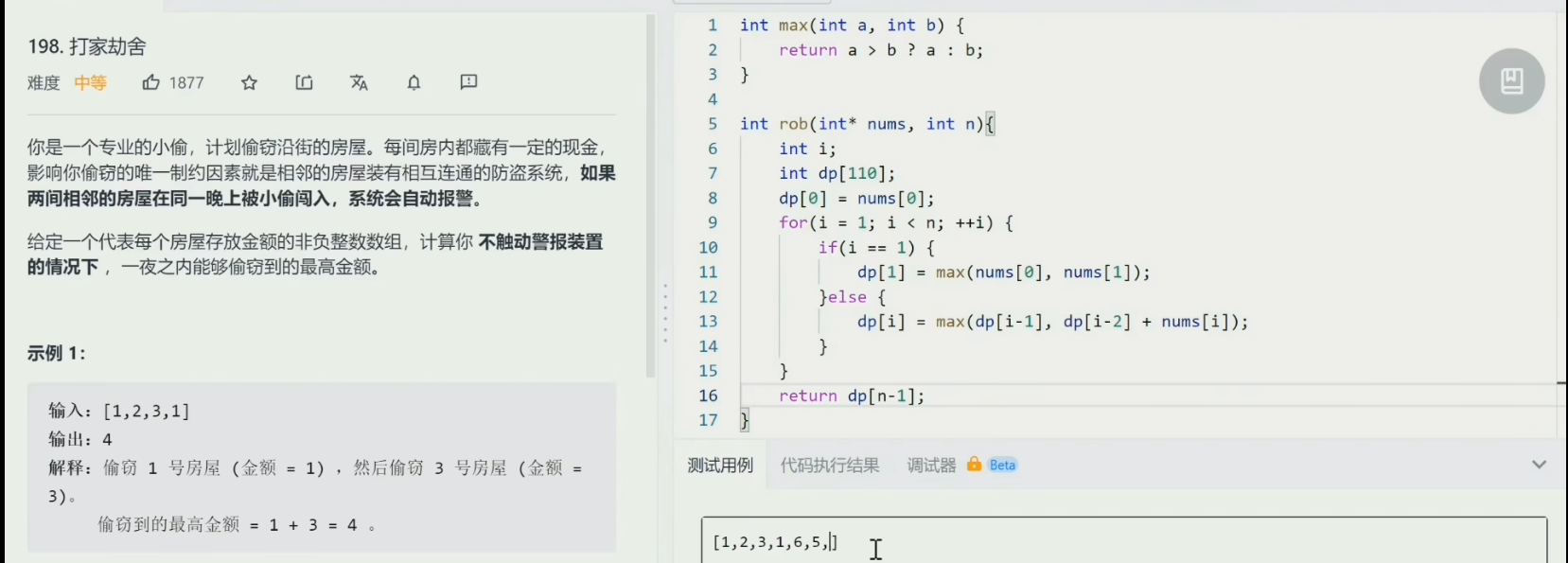
动态规划（未完成）
https://www.bilibili.com/video/BV1XR4y1j7Lo?spm_id_from=333.788.videopod.sections&vd_source=2a065d0754c6c2db7ab56846a1452e9f
刷动态规划题目的大致流程：
1、设计状态(从最简单的情况开始找，在逐步增加；每一步依靠以前的最优解得到现在的步骤)
2、写出状态转移方程
3、设定初始状态
4、执行状态转移
5、返回最终的解
映射
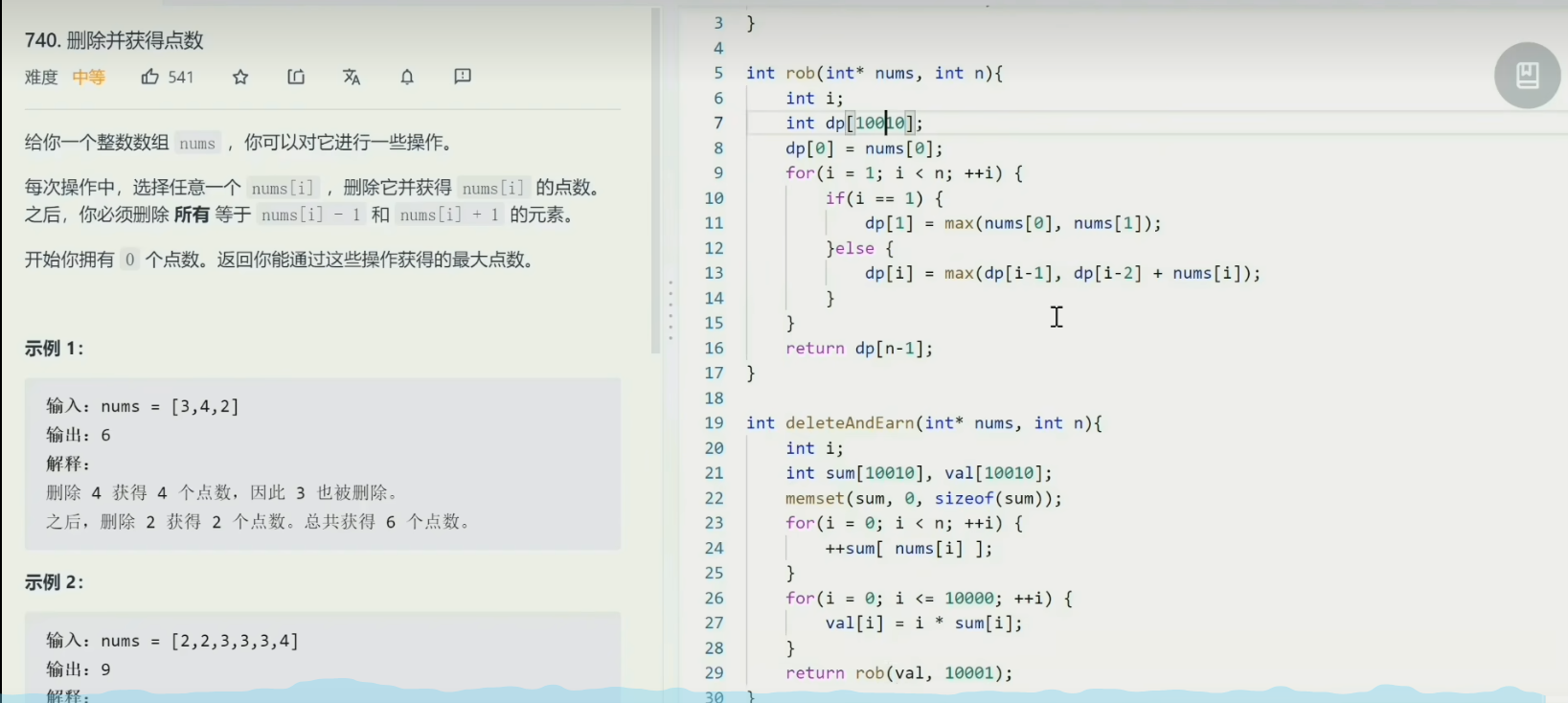
一个例题：找零
动态规划解法：
动态规划算法采用了一种更有条理的方式来得到问题的解
找零兑换的动态规划算法从最简单的“1分钱找零”的最优解开始，逐步递加上去，直到我们需要的找零钱数
在找零递加的过程中，设法保持每一分钱的递加都是最优解，一直加到求解找零钱数，自然得到最优解
问题的最优解包含了更小规模子问题的最优解，这是一个最优化问题能够用动态规划策略解决的必要条件
def dpMakeChange(coinValueList, change, minCoins):
# 从1分开始到change逐个计算最少硬币数
for cents in range(1, change + 1):
# 1. 初始化一个最大值
coinCount = cents
# 2. 减去每个硬币，向后查最少硬币数，同时记录总的最少的数
for j in [c for c in coinValueList if c <= cents]:
if minCoins[cents - j] + 1 < coinCount:
coinCount = minCoins[cents - j] + 1
# 3. 得到当前最少硬币数，记录到表中
minCoins[cents] = coinCount
# 返回最后一个结果
return minCoins[change]
print(dpMakeChange([1, 5, 10, 21, 25], 63, [0] * 64))
找零兑换：动态规划算法扩展
✓ 前面的算法已经得到了最少硬币的数量，但没有返回硬币如何组合。
✓ 扩展算法的思路很简单，只需要在生成最优解列表同时跟踪记录所选择的那个硬币币值即可。
✓ 在得到最后的解后，减去选择的硬币币值，回溯到表格之前的部分找零，就能逐步得到每一步所选择的硬币币值。
# 定义金额和硬币面额列表
amt = 63
clist = [1, 5, 10, 21, 25]
# 初始化两个列表，用于记录使用的硬币和硬币数量
coinsUsed = [0] * (amt + 1)
coinCount = [0] * (amt + 1)
# 打印标题
print("Making change for", amt, "requires")
# 调用函数计算最少硬币数量并记录使用的硬币
def dpMakeChange(coinValueList, change, minCoins, coinsUsed):
for cents in range(change + 1):
coinCount = cents
newCoin = 1
for j in [c for c in coinValueList if c <= cents]:
if minCoins[cents - j] + 1 < coinCount:
coinCount = minCoins[cents - j] + 1
newCoin = j
minCoins[cents] = coinCount
coinsUsed[cents] = newCoin
return minCoins[change]
result = dpMakeChange(clist, amt, coinCount, coinsUsed)
print("They are:")
# 打印使用的硬币
def printCoins(coinsUsed, change):
coin = change
while coin > 0:
thisCoin = coinsUsed[coin]
print(thisCoin)
coin = coin - thisCoin
printCoins(coinsUsed, amt)
print("The used list is as follows:")
print(coinsUsed)
