薇尔莉特的打字机题解

薇尔莉特的打字机题解

好题(就是我死活想不到，看题解后却不得不佩服思路巧妙的题)；
我们将一种字符串看做一个点；
每一次操作就是对所有存在的点进行拓展
-->不按，状态不变；
-->按下，状态增加；

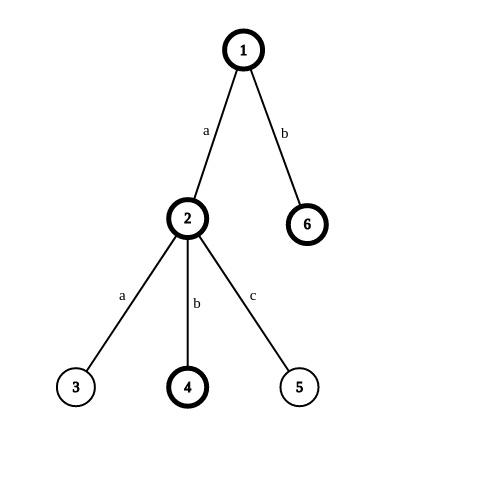
这就是先按a后按b的例子。
1.输入一个字母：
所有子树中没有此字母的点会增加，
所以我们用一个数组\(f[x]\)记载没有此字母\(x\)的点数
之后，原来的所有点都有此字母了，新增的点一定没有。
2.删除：
因为每次打字都有可能不输入进去，所以删除增加的状态只可能是，删去所有操作的打字后，再删去原来的字母。
状态数和没此字母的状态都加1

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=5e6+7,mod=19260817;
int n,m;
char a[N],b[N];
ll t,ans=1,f[30];
inline int read(){
   int T=0,F=1; char ch=getchar();
   while(ch<'0'||ch>'9'){if(ch=='-') F=-1; ch=getchar();}
   while(ch>='0'&&ch<='9') T=(T<<3)+(T<<1)+(ch-48),ch=getchar();
   return F*T;
}
int main(){
   n=read(),m=read(),scanf("%s%s",a+1,b+1),f[0]=1;
   for(int i=1;i<=m;++i){
       if(b[i]>='A'&&b[i]<='Z') t=f[b[i]-64],f[b[i]-64]=ans,ans=((ans+ans-t)%mod+mod)%mod;
       else{
           if(!n) continue;
           f[a[n]-64]=(f[a[n]-64]+1ll)%mod,ans=(ans+1ll)%mod,--n;
       } 
   }
   printf("%lld\n",ans);
   return 0;
}