失昼城的守星使题解

失昼城的守星使题解

题目链接
好恶心啊～
不过这么恶心的题我居然能一遍A(虽然自己造数据调了一天)
而且还没看题解，想想就激动。
不过题目又臭又长，我来化简一下吧：
有n个岛，成树形结构，岛上可住人、可不住人，
每次修改，将一个岛上的人赶出去，或住满人；
每次询问，求所有住人的岛到\(x\)到\(y\)的路径上的距离之和。
恶心至极，恶心至极，恶心至极(重要的事情说三遍)
我们可将其转化一下，变为每条边的边权*经过它的次数
拿图来说吧：

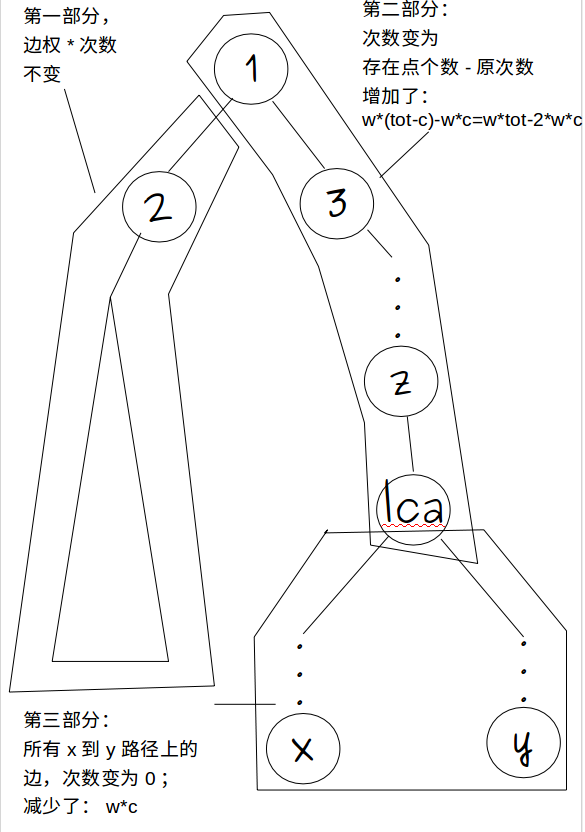
我们拿\(sum\)表示边权×次数，\(w\)表示边权和：
最终式子变为:到点1的边权×次数和-第三部分的边权×次数和-2×第二部分边权×次数和+总存在点数×第二部分边权和；
恶心吧。
别急，还有修改操作呢(只不过简单多了)；
1.将一个点由不存在变存在：1到此点的边的次数都加1（区间的边权×次数和加上边权和）
2.将一个点由存在变为不存在：1到此点的边的次数都减1（区间的边权×次数和减去边权和）

#include<bits/stdc++.h>
#define ll long long
#define lc x<<1
#define rc x<<1|1
using namespace std;
const int N=2e5+7;
int n,m,t1,t2,t3,LCA,opt,cnt=0,dfn=0,a[N],f[N],d[N],top[N],son[N],num[N],head[N],siz2[N];
ll tot=0,ttt,siz[N],v[N],pw[N],sw[N];
struct tree{ll w,sum,lazy;}t[N<<2];
struct edge{int nxt,to,w;}e[N<<1];
inline void add(int u,int v,int w){e[++cnt].nxt=head[u],e[cnt].to=v,e[cnt].w=w,head[u]=cnt;}
inline void modify(int x,ll y){t[x].lazy+=y,t[x].w+=t[x].sum*y;}
inline void pushdown(int x){if(t[x].lazy) modify(lc,t[x].lazy),modify(rc,t[x].lazy),t[x].lazy=0;}
inline int read(){
   int T=0,F=1; char ch=getchar();
   while(ch<'0'||ch>'9'){if(ch=='-') F=-1; ch=getchar();}
   while(ch>='0'&&ch<='9') T=(T<<3)+(T<<1)+(ch-48),ch=getchar();
   return F*T;   
}
void build(int l,int r,int x){
     if(l==r){t[x].sum=pw[l],t[x].w=v[l]; return;}
     int mid=l+r>>1;
     build(l,mid,lc),build(mid+1,r,rc);
     t[x].w=t[lc].w+t[rc].w,t[x].sum=t[lc].sum+t[rc].sum;
}
void update(int l,int r,int p,int q,int x,ll y){
    if(p<=l&&r<=q){modify(x,y); return;}
    int mid=l+r>>1; pushdown(x);
    if(p<=mid) update(l,mid,p,q,lc,y);
    if(q>mid) update(mid+1,r,p,q,rc,y);
    t[x].w=t[lc].w+t[rc].w;
}
ll query(int l,int r,int p,int q,int x){
   if(p>q) return 0;
   if(p<=l&&r<=q) return t[x].w;
   int mid=l+r>>1; ll ans=0; pushdown(x);
   if(p<=mid) ans=query(l,mid,p,q,lc);
   if(q>mid) ans+=query(mid+1,r,p,q,rc);
   return ans;
}
ll query2(int l,int r,int p,int q,int x){
   if(p>q) return 0;
   if(p<=l&&r<=q) return t[x].sum;
   int mid=l+r>>1; ll ans=0; pushdown(x);
   if(p<=mid) ans=query2(l,mid,p,q,lc);
   if(q>mid) ans+=query2(mid+1,r,p,q,rc);
   return ans;
}
void lj_update(int x,int y){
    int pp=a[y]?-1:1;
    while(top[x]!=top[y]){
       if(d[top[x]]<d[top[y]]) swap(x,y);
       update(1,n,num[top[x]],num[x],1,pp);
       x=f[top[x]];
    }
    if(d[x]>d[y]) swap(x,y);
    update(1,n,num[x],num[y],1,pp); 
}
ll lj_query2(int x,int y){
   ll ans=0;
   while(top[x]!=top[y]){
      if(d[top[x]]<d[top[y]]) swap(x,y);
      ans+=query2(1,n,num[top[x]],num[x],1);
      x=f[top[x]];
   }
   if(d[x]>d[y]) swap(x,y);
   ans+=query2(1,n,num[x]+1,num[y],1);
   return ans;
}
ll lj_query(int x,int y){
   ll ans=0;
   while(top[x]!=top[y]){
      if(d[top[x]]<d[top[y]]) swap(x,y);
      ans+=query(1,n,num[top[x]],num[x],1);
      x=f[top[x]];
   }
   if(d[x]>d[y]) swap(x,y);
   ans+=query(1,n,num[x]+1,num[y],1),LCA=x;
   return ans;
}
ll get_ans(int x,int y){
   ttt=lj_query(x,y); t3=LCA; 
   return t[1].w-ttt-2ll*lj_query(1,t3)+tot*lj_query2(1,t3); 
}
void dfs(int x,int fa){
    f[x]=fa,d[x]=d[fa]+1,siz[x]=a[x],siz2[x]=1; int maxt=0; ll tt=0;
    for(int i=head[x];i;i=e[i].nxt)
        if(e[i].to!=fa){
           dfs(e[i].to,x),siz[x]+=siz[e[i].to],siz2[x]+=siz2[e[i].to];
           if(siz2[maxt]<siz2[e[i].to]) maxt=e[i].to,tt=e[i].w;
        }
    son[x]=maxt,sw[x]=tt;
}
void dfs2(int x,int topx,ll ww){
    ++dfn,num[x]=dfn,v[dfn]=ww*siz[x],pw[dfn]=ww,top[x]=topx;
    if(son[x]) dfs2(son[x],topx,sw[x]);
    for(int i=head[x];i;i=e[i].nxt) if(e[i].to!=son[x]&&e[i].to!=f[x]) dfs2(e[i].to,e[i].to,e[i].w); 
}
int main(){
    n=read(),m=read(),ttt=read();
    for(int i=1;i<n;++i) t1=read(),t2=read(),t3=read(),add(t1,t2,t3),add(t2,t1,t3);
    for(int i=1;i<=n;++i) a[i]=read();
    dfs(1,0),dfs2(1,1,0),build(1,n,1),tot=siz[1];
    for(int i=1;i<=m;++i){
        opt=read(),t1=read();
        if(opt==1) tot=tot+(a[t1]?-1:1),lj_update(1,t1),a[t1]=!a[t1];
        else t2=read(),printf("%lld\n",get_ans(t1,t2));
    }
    return 0;
}