李超树学习笔记

李超树学习笔记

这东西有点恶心啊，搞了好久才懂一点。
1.有什么用？
对于一个区间\([l,r]\)每个点可以取的权值符合表达式:\(y=kx+b\)的线段
有k条线段覆盖在所有点上，可以动态插入线段，求每个时刻某个点或某个区间的最大/最小值。
它的思想是：尽可能不将优势线段下传，
2.什么叫优势线段？(假如是使每个点的值最大)

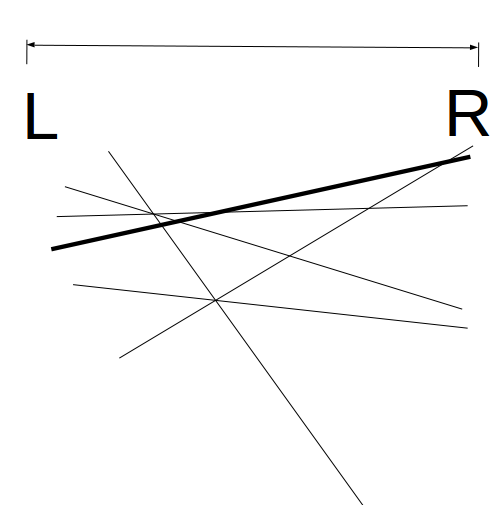
就是使区间内的取最大值的点最多的线段(当然，我们每次在实际操作中只是将优势线段与插入线段进行比较，这里的多条线段只是为了方便理解，两条线段的图如下：)

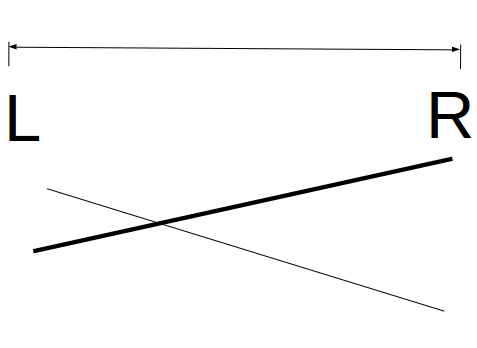
3.如何实现？
我们可以分成4种情况讨论：(以最大值为标准)
\(<1>.\)插入线段的斜率大于原有优势线段：
\((1).\)交点在区间中点左边:

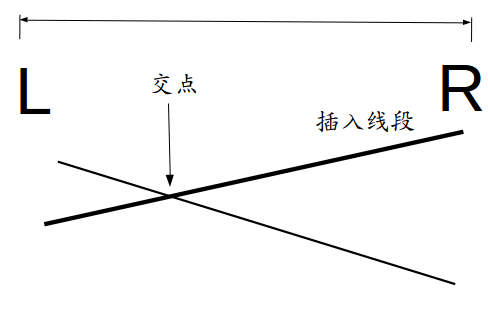
显然，优势线段改为插入线段，但原优势线段可能在左子区间更优，递归。
此时中点处y值插入线段大于原优势线段。
\((2).\)交点在区间中点右边:

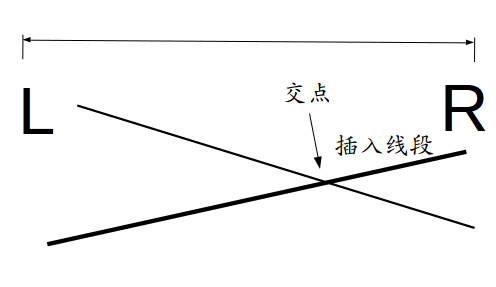
插入线段在此区间没有原优势线段优，但在右子区间有希望更优，递归。
此时中点处y值插入线段小于原优势线段。
\(<2>.\)插入线段的斜率小于原有优势线段：
\((1).\)交点在区间中点左边:

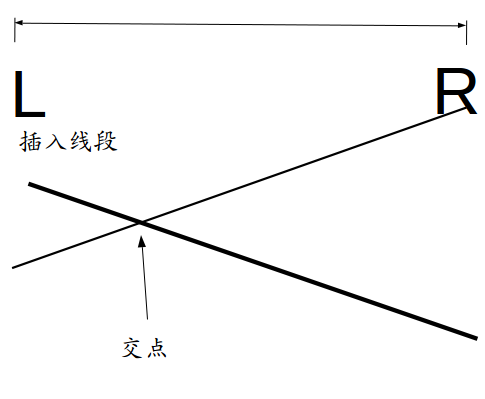
插入线段在此区间没有原优势线段优，但在左子区间有希望更优，递归。
此时中点处y值插入线段小于原优势线段。
\((2).\)交点在区间中点右边:

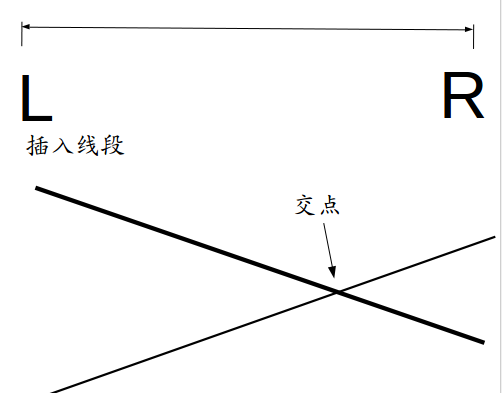
显然，优势线段改为插入线段，但原优势线段可能在右子区间更优，递归。
此时中点处y值插入线段大于原优势线段。
修改大概就这样，下面是代码：
单点修改：

void update(int l,int r,int id,int x){
    if(l==r){if(f(id,l)>f(tag[x],l)) tag[x]=id; return;}
    int mid=l+r>>1;
    if(line[tag[x]].p>line[id].p){
       if(f(tag[x],mid)<f(id,mid)) update(mid+1,r,tag[x],rc),tag[x]=id;
       else update(l,mid,id,lc);
    }
    else{
       if(f(tag[x],mid)<f(id,mid)) update(l,mid,tag[x],lc),tag[x]=id;
       else update(mid+1,r,id,rc);
    }
}

区间修改：

void update(int l,int r,int p,int q,int id,int x){
    int mid=l+r>>1;
    if(p<=l&&r<=q){
       if(l==r){if(f(id,l)>f(tag[x],l)) tag[x]=id; return;}
       if(line[tag[x]].p>line[id].p){
           if(f(tag[x],mid)<f(id,mid)) update(mid+1,r,mid+1,r,tag[x],rc),tag[x]=id;
           else update(l,mid,l,mid,id,lc);
       }
       else{
          if(f(tag[x],mid)<f(id,mid)) update(l,mid,l,mid,tag[x],lc),tag[x]=id;
          else update(mid+1,r,mid+1,r,id,rc);
       }
       return;
    }
    if(p<=mid) update(l,mid,p,q,id,lc);
    if(q>mid) update(mid+1,r,p,q,id,rc);
}

但是如果是区间查询则要加上维护区间最小值/最大值的数组：
十分麻烦，是我太蒟蒻了
首先我们要明确区间的最值一般都在两端，
所以我们有些 没有更新下去的要自我用两端的最值更新，

void update(int l,int r,int p,int q,ll k,ll b,int x){
     int mid=l+r>>1;
     if(p<=l&&r<=q){
        if(l==r){if(k*w[l]+b<f(t[x],w[l])) t[x].k=k,t[x].b=b,t[x].minx=f(t[x],w[l]); return;}
        if(k>t[x].k){
           if(k*w[mid]+b<f(t[x],w[mid])) update(mid+1,r,p,q,t[x].k,t[x].b,rc),t[x].k=k,t[x].b=b;
           else update(l,mid,p,q,k,b,lc);
        }
        else{
           if(k*w[mid]+b<f(t[x],w[mid])) update(l,mid,p,q,t[x].k,t[x].b,lc),t[x].k=k,t[x].b=b;
           else update(mid+1,r,p,q,k,b,rc);
        }
        t[x].minx=min(t[x].minx,min(f(t[x],w[l]),f(t[x],w[r]))),t[x].minx=min(t[x].minx,min(t[lc].minx,t[rc].minx));
        return;
     }
     if(p<=mid) update(l,mid,p,q,k,b,lc);
     if(q>mid) update(mid+1,r,p,q,k,b,rc);
     t[x].minx=min(t[x].minx,min(t[lc].minx,t[rc].minx));
}

由于我们优势线段能不下传就不下传，
所以使某点/某区间最优的线段可能在父区间上，
故要用父区间的和它比较。
单点查询：

double query(int l,int r,int p,int x){
    if(l==r) return f(tag[x],l);
    int mid=l+r>>1; double ans=f(tag[x],p);
    if(p<=mid) return max(ans,query(l,mid,p,lc));
    return max(ans,query(mid+1,r,p,rc));
}

区间查询：

ll query(int l,int r,int p,int q,int x){
   if(p<=l&&r<=q) return t[x].minx;
   int mid=l+r>>1; ll ans=inf;
   if(t[x].b!=inf){
      int u=max(l,p),v=min(r,q);
      ans=min(f(t[x],w[u]),f(t[x],w[v]));
   }
   if(p<=mid) ans=min(ans,query(l,mid,p,q,lc));
   if(q>mid) ans=min(ans,query(mid+1,r,p,q,rc));
   return ans;
}