Sonya and Ice Cream题解

Sonya and Ice Cream题解

这道题是一位一遍A了快餐店的巨佬推荐给我的，说快餐店巨简单，不过还是先做一下简化版，就是这道题（照顾我太弱了）
好了回到这一题，
首先，这条路径一定在直径上(若有一段不是直径，一定比直径的长)
巨佬说随便画图理解一下就行了
然后我们可以二分答案x(最小的最大值)，
贪心找到离直径一端距离<=x的最远点(倍增)，
情况大概如下图：

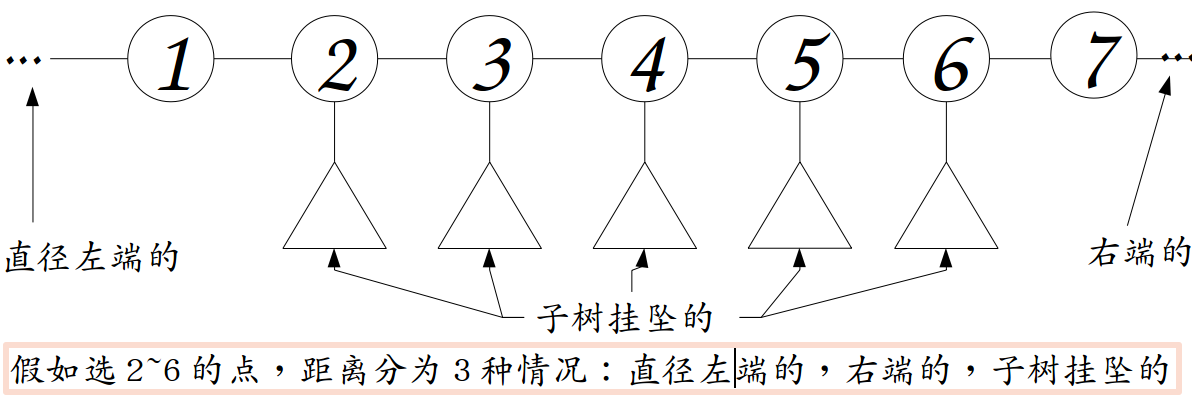
其中子树挂坠，将直径看为序列用ST表预处理
左端的直径，因为从左端跑起，所以一定小于x，
右端的直径，用前缀和维护序列距离，
最后具体实现细节在代码里：

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+6;
int n,k,t1,t2,t3,fr,cnt=0,head[N],v[N],f[N][21],g[N][21];
int maxp=0,maxt=0,maxdis[N],a[N],sum[N],len,deep,w[N],h[N][21];
struct edge{int nxt,to,w;}e[N<<1];
inline void add(int u,int v,int w){e[++cnt].nxt=head[u],e[cnt].to=v,e[cnt].w=w,head[u]=cnt;}
inline int read(){
   int T=0,F=1; char ch=getchar();
   while(ch<'0'||ch>'9'){if(ch=='-') F=-1; ch=getchar();}
   while(ch>='0'&&ch<='9') T=(T<<3)+(T<<1)+(ch-48),ch=getchar();
   return F*T; 
}
void dfs(int x,int fa,int w){
    sum[x]=w;
    for(int i=head[x];i;i=e[i].nxt) if(e[i].to!=fa) dfs(e[i].to,x,w+e[i].w);
    if(maxp<w) maxp=w,maxt=x;
}
void dfs2(int x,int fa,int d){
    maxdis[x]=0,f[x][0]=fa;
    for(int i=1;i<=20;++i) f[x][i]=f[f[x][i-1]][i-1],g[x][i]=g[x][i-1]+g[f[x][i-1]][i-1];
    for(int i=head[x];i;i=e[i].nxt) if(e[i].to!=fa) g[e[i].to][0]=e[i].w,dfs2(e[i].to,x,d+1),v[x]|=v[e[i].to],maxdis[x]=(!v[e[i].to]?max(maxdis[x],maxdis[e[i].to]+e[i].w):maxdis[x]);
    if(v[x]) a[d]=x,deep=max(deep,d);
}
bool check(int x){
    t1=maxt,t2=x,cnt=0;
    for(int i=20;i>=0;--i) if(t2>=g[t1][i]) t2-=g[t1][i],t1=f[t1][i],cnt+=(1<<i);
    //贪心求出离直径深度为deep的点距离<=x的最远点，看一看它到后面的k-1个点的路径上挂坠子树的最大距离，和路径上最后一个点到直径另一端(深度为1)的距离是否小于等于x
    t3=max(deep-cnt-k+1,1);//t3为路径上第k个点
    return max(sum[a[t3]],w[t3])<=x;
}
int ef(int l,int r){
    if(l==r) return l;
    int mid=l+r>>1;
    if(check(mid)) return ef(l,mid);
    return ef(mid+1,r);
}
int main(){
   n=read(),k=read();
   for(int i=1;i<n;++i) t1=read(),t2=read(),t3=read(),add(t1,t2,t3),add(t2,t1,t3);
   dfs(1,0,0);
   maxp=0,fr=maxt,maxt=0,dfs(fr,0,0);
   //求直径，从fr到maxt，长度为maxp,求出sum数组代表直径上深度为i的点到深度为1的点(直径端点)的距离
   v[maxt]=1,deep=0,dfs2(fr,0,1);
   //第二遍搜直径上的点，看成序列存在a里，编号即为深度，预处理倍增数组
   for(int i=deep;i>=1;--i) h[i][0]=maxdis[a[i]];
   for(int i=1;i<=20;++i) for(int j=1;j+(1<<i)-1<=deep;++j) h[j][i]=max(h[j][i-1],h[j+(1<<(i-1))][i-1]);
   for(int i=1;i<=deep;++i) len=(int)log2(min(deep-i+1,k)),w[i]=max(h[i][len],h[i+k-(1<<len)][len]);
   //ST表求直径上挂坠的子树的最大距离
   printf("%d\n",ef(0,1e9));
   //二分求解
   return 0;
}

最后我发现似乎可以在二分里直接\(O(n)\)扫一遍不要预处理(某位巨佬坑我),我苦心追求的\(O((log n)^{2})\)的复杂度也因为预处理变成\(O(n log n)\)了
WuWuWu~~
这个故事告诉我们，千万不要追求优秀时间复杂度啊
附简单代码:

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+6;
int n,k,t1,t2,t3,fr,cnt=0,head[N],v[N];
int maxp=0,maxt=0,maxdis[N],a[N],sum[N],deep;
struct edge{int nxt,to,w;}e[N<<1];
inline void add(int u,int v,int w){e[++cnt].nxt=head[u],e[cnt].to=v,e[cnt].w=w,head[u]=cnt;}
inline int read(){
   int T=0,F=1; char ch=getchar();
   while(ch<'0'||ch>'9'){if(ch=='-') F=-1; ch=getchar();}
   while(ch>='0'&&ch<='9') T=(T<<3)+(T<<1)+(ch-48),ch=getchar();
   return F*T; 
}
void dfs(int x,int fa,int w){
    sum[x]=w;
    for(int i=head[x];i;i=e[i].nxt) if(e[i].to!=fa) dfs(e[i].to,x,w+e[i].w);
    if(maxp<w) maxp=w,maxt=x;
}
void dfs2(int x,int fa,int d){
    maxdis[x]=0;
    for(int i=head[x];i;i=e[i].nxt) if(e[i].to!=fa) dfs2(e[i].to,x,d+1),v[x]|=v[e[i].to],maxdis[x]=(!v[e[i].to]?max(maxdis[x],maxdis[e[i].to]+e[i].w):maxdis[x]);
    if(v[x]) a[d]=x,deep=max(deep,d);
}
bool check(int x){
    t1=1,t3=0,t2=a[1];
    for(int i=deep;i>=1;--i) if(sum[a[deep]]-sum[a[i]]>x){t1=i+1; break;}
    for(int i=t1;i>=max(t1-k+1,1);--i) t3=max(maxdis[a[i]],t3),t2=a[i];
    return max(sum[t2],t3)<=x;
}
int ef(int l,int r){
    if(l==r) return l;
    int mid=l+r>>1;
    if(check(mid)) return ef(l,mid);
    return ef(mid+1,r);
}
int main(){
   n=read(),k=read();
   for(int i=1;i<n;++i) t1=read(),t2=read(),t3=read(),add(t1,t2,t3),add(t2,t1,t3);
   dfs(1,0,0);
   maxp=0,fr=maxt,maxt=0,dfs(fr,0,0);
   v[maxt]=1,deep=0,dfs2(fr,0,1);
   printf("%d\n",ef(0,1e9));
   return 0;
}