CF1140G Double Tree题解

CF1140G Double Tree题解

我实在太弱了，想不出看题解竟然看不懂\(O(n)\)做法，不过好歹得到了一点启发，自己写下了\(O(nlog_{n})\)的倍增的极其丑陋的代码：
预处理大部分思路跟楼上巨佬相同,
将图视作两棵树，一棵全是奇点，编号为0，一棵全是偶点，编号为1，两部分的对应点之间一一有边相连。
先求出两棵树对应点之间的最小距离，
用两遍\(dfs\)，一遍\(dfs\)求出走子树的对应点之间的最小距离，另一遍\(dfs3\)在此基础上看看是否能通过走父辈节点来更新最小距离。

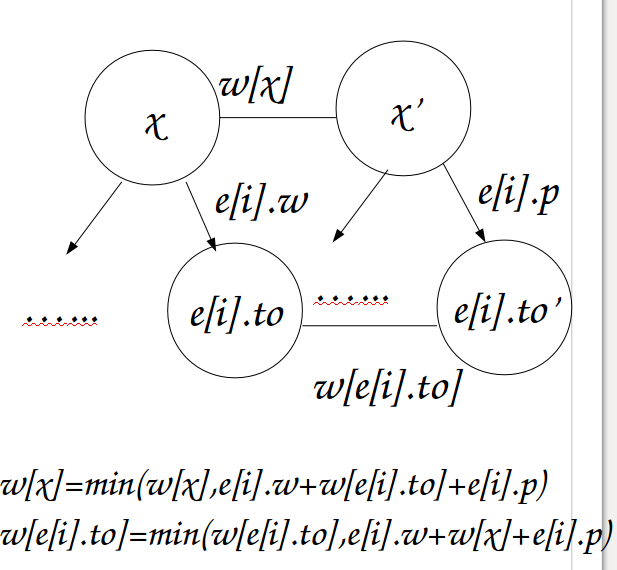
接下来dfs2遍历预处理出倍增数组：
\(g[x][y][z]\)代表\(y\)和\(y*2^{n}\)的状态为\(x\)，\(y\)为当前点，\(z\)是倍增数。
其中
\(\left\{\begin{matrix} x=0:y\in {tree_{0}},z\in {tree_{0}} & \\x=1:y\in {tree_{1}},z\in {tree_{0}} & \\x=2:y\in {tree_{0}},z\in {tree_{1}} & \\x=3:y\in {tree_{1}},z\in {tree_{1}} & \end{matrix}\right.\)
由此我们可以推断出核心代码：
\(\left\{\begin{matrix} g[0][x][i]=min(g[0][x][i-1]+g[0][f[x][i-1]][i-1],g[2][x][i-1]+g[1][f[x][i-1]][i-1]); \\g[1][x][i]=min(g[1][x][i-1]+g[0][f[x][i-1]][i-1],g[3][x][i-1]+g[1][f[x][i-1]][i-1]); \\g[2][x][i]=min(g[0][x][i-1]+g[2][f[x][i-1]][i-1],g[2][x][i-1]+g[3][f[x][i-1]][i-1]); \\g[3][x][i]=min(g[1][x][i-1]+g[2][f[x][i-1]][i-1],g[3][x][i-1]+g[3][f[x][i-1]][i-1]); \end{matrix}\right.\)
举个栗子：

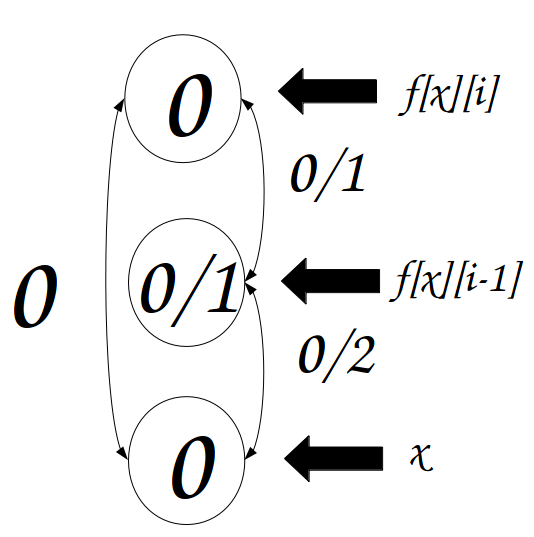
\(g[0][x][i]\)便可能由\(g[0][x][i-1],g[0][f[x][i-1][i-1]]\)和\(g[2][x][i-1],g[1][f[x][i-1]][i-1]\)转移过来
至于后面\(lca\)操作\(ans[][][]\)的转移，
只是样子看起来和这个有点不一样，本质是相同的。
记得注意一下\(ans[][][]\)的初值，想想为什么这么赋。
还有返回值，记得\(lca\)的状态要一致，故只有两种状态。

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=3e5+6;
const ll inf=2e17;
int n,q,t1,t2,cnt=0,head[N],f[N][21],d[N];
ll t3,t4,w[N],g[4][N][21];
struct edge{int nxt,to; ll w,p;}e[N<<1];
inline void add(int u,int v,ll w,ll p){e[++cnt].nxt=head[u],e[cnt].to=v,e[cnt].w=w,e[cnt].p=p,head[u]=cnt;}
inline ll read(){
   ll F=1,T=0; char ch=getchar(); 
   while(ch<'0'||ch>'9'){if(ch=='-') F=-1; ch=getchar();}
   while(ch>='0'&&ch<='9') T=(T<<3)+(T<<1)+(ch-48),ch=getchar();
   return F*T;
}
void dfs(int x,int fa){for(int i=head[x];i;i=e[i].nxt) if(e[i].to!=fa) dfs(e[i].to,x),w[x]=min(w[x],w[e[i].to]+e[i].w+e[i].p);}
void dfs3(int x,int fa){for(int i=head[x];i;i=e[i].nxt) if(e[i].to!=fa) w[e[i].to]=min(w[e[i].to],w[x]+e[i].w+e[i].p),dfs3(e[i].to,x);}
void dfs2(int x,int fa){
     f[x][0]=fa,d[x]=d[fa]+1;
     for(int i=1;i<=20;++i){
         f[x][i]=f[f[x][i-1]][i-1];
         g[0][x][i]=min(g[0][x][i-1]+g[0][f[x][i-1]][i-1],g[2][x][i-1]+g[1][f[x][i-1]][i-1]),g[1][x][i]=min(g[1][x][i-1]+g[0][f[x][i-1]][i-1],g[3][x][i-1]+g[1][f[x][i-1]][i-1]);
         g[2][x][i]=min(g[0][x][i-1]+g[2][f[x][i-1]][i-1],g[2][x][i-1]+g[3][f[x][i-1]][i-1]),g[3][x][i]=min(g[1][x][i-1]+g[2][f[x][i-1]][i-1],g[3][x][i-1]+g[3][f[x][i-1]][i-1]);
     }
     for(int i=head[x];i;i=e[i].nxt)
         if(e[i].to!=fa){
            g[0][e[i].to][0]=min(e[i].w,w[e[i].to]+e[i].p+w[x]),g[3][e[i].to][0]=min(e[i].p,w[e[i].to]+e[i].w+w[x]);
            g[1][e[i].to][0]=min(e[i].p+w[x],e[i].w+w[e[i].to]),g[2][e[i].to][0]=min(e[i].p+w[e[i].to],e[i].w+w[x]),dfs2(e[i].to,x); 
         }
}
ll lca(int u,int v,int x,int y){
   int pp=0,qq=0;
   if(u==v) return w[u];
   if(d[u]<d[v]) swap(u,v),swap(x,y);
   ll ans[2][2][4]; memset(ans,0,sizeof(ans)),ans[0][0][x^1]=ans[0][0][2+(x^1)]=inf,ans[0][1][y^1]=ans[0][1][2+(y^1)]=inf;
   if(x==1) ans[0][0][1]=inf;
   else ans[0][0][2]=inf;
   if(y==1) ans[0][1][1]=inf;
   else ans[0][1][2]=inf;
   for(int i=20;i>=0;--i)
       if(d[u]>=d[v]+(1<<i)){
          pp^=1;
          ans[pp][0][0]=min(ans[pp^1][0][0]+g[0][u][i],ans[pp^1][0][2]+g[1][u][i]),ans[pp][0][1]=min(ans[pp^1][0][1]+g[0][u][i],ans[pp^1][0][3]+g[1][u][i]);
          ans[pp][0][2]=min(ans[pp^1][0][0]+g[2][u][i],ans[pp^1][0][2]+g[3][u][i]),ans[pp][0][3]=min(ans[pp^1][0][1]+g[2][u][i],ans[pp^1][0][3]+g[3][u][i]),u=f[u][i];
       }
   if(u==v) return ans[pp][0][x+(y<<1)];
   for(int i=20;i>=0;--i)
       if(f[u][i]!=f[v][i]){
          pp^=1,qq^=1;
          ans[qq][1][0]=min(ans[qq^1][1][0]+g[0][v][i],ans[qq^1][1][2]+g[1][v][i]),ans[qq][1][1]=min(ans[qq^1][1][1]+g[0][v][i],ans[qq^1][1][3]+g[1][v][i]);
          ans[qq][1][2]=min(ans[qq^1][1][0]+g[2][v][i],ans[qq^1][1][2]+g[3][v][i]),ans[qq][1][3]=min(ans[qq^1][1][1]+g[2][v][i],ans[qq^1][1][3]+g[3][v][i]),v=f[v][i];
          ans[pp][0][0]=min(ans[pp^1][0][0]+g[0][u][i],ans[pp^1][0][2]+g[1][u][i]),ans[pp][0][1]=min(ans[pp^1][0][1]+g[0][u][i],ans[pp^1][0][3]+g[1][u][i]);
          ans[pp][0][2]=min(ans[pp^1][0][0]+g[2][u][i],ans[pp^1][0][2]+g[3][u][i]),ans[pp][0][3]=min(ans[pp^1][0][1]+g[2][u][i],ans[pp^1][0][3]+g[3][u][i]),u=f[u][i];
       }
   pp^=1,qq^=1;
   ans[qq][1][0]=min(ans[qq^1][1][0]+g[0][v][0],ans[qq^1][1][2]+g[1][v][0]),ans[qq][1][1]=min(ans[qq^1][1][1]+g[0][v][0],ans[qq^1][1][3]+g[1][v][0]);
   ans[qq][1][2]=min(ans[qq^1][1][0]+g[2][v][0],ans[qq^1][1][2]+g[3][v][0]),ans[qq][1][3]=min(ans[qq^1][1][1]+g[2][v][0],ans[qq^1][1][3]+g[3][v][0]),v=f[v][0];
   ans[pp][0][0]=min(ans[pp^1][0][0]+g[0][u][0],ans[pp^1][0][2]+g[1][u][0]),ans[pp][0][1]=min(ans[pp^1][0][1]+g[0][u][0],ans[pp^1][0][3]+g[1][u][0]);
   ans[pp][0][2]=min(ans[pp^1][0][0]+g[2][u][0],ans[pp^1][0][2]+g[3][u][0]),ans[pp][0][3]=min(ans[pp^1][0][1]+g[2][u][0],ans[pp^1][0][3]+g[3][u][0]),u=f[u][0];
   return min(ans[pp][0][x]+ans[qq][1][y],ans[pp][0][x+2]+ans[qq][1][y+2]);
}
int main(){
    n=read();
    for(int i=1;i<=n;++i) w[i]=read();
    for(int i=1;i<n;++i) t1=read(),t2=read(),t3=read(),t4=read(),add(t1,t2,t3,t4),add(t2,t1,t3,t4);
    dfs(1,0),dfs3(1,0),dfs2(1,0),q=read();
    for(int i=1;i<=q;++i) t1=read(),t2=read(),printf("%lld\n",lca((t1+1)>>1,(t2+1)>>1,!(t1&1),!(t2&1)));
    return 0;
}