树上游戏题解
树上游戏题解
@ sxd666888巨佬,太巨了,\(O(n)\)做法虐爆全场。
但是细节有点没讲清楚(我理解能力太差了)
我来补充一下细节(大佬认为我们理所应当理解的东西)
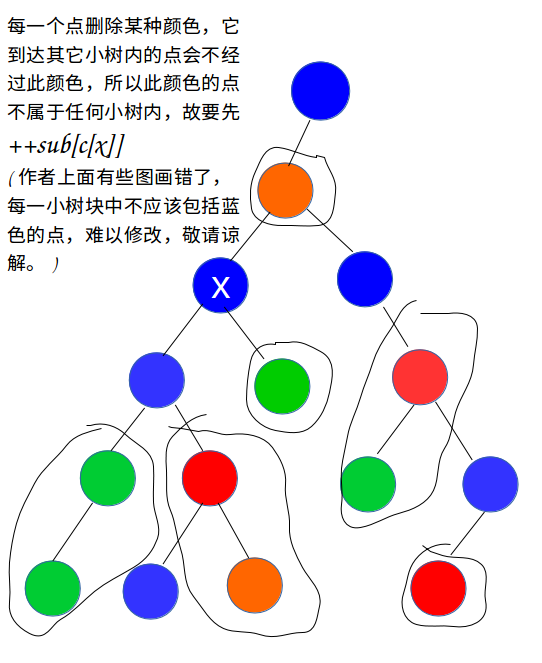
\(upd:\)(作者上面有些图画错了,每一小树块中不应该包括蓝色的点,难以修改,敬请谅解。)
首先,删除某一种颜色会形成很多棵小树,
注意:此文中小树跟子树不同。
我们若将每种颜色的贡献看为这条路径上的第一个点,
那么,
每棵小树中的所有点到其它小树上的任意点都会经过这棵小树的根的父亲,
会有一次贡献。
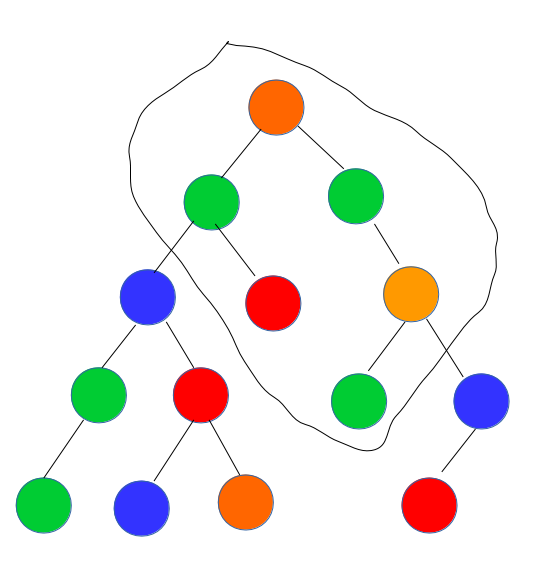
如图样例:
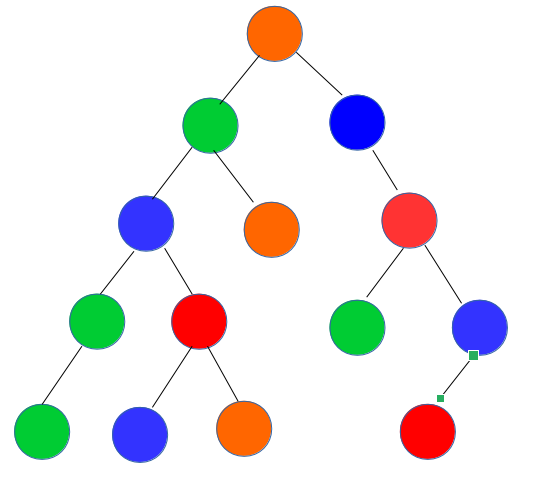
删除蓝色点后:
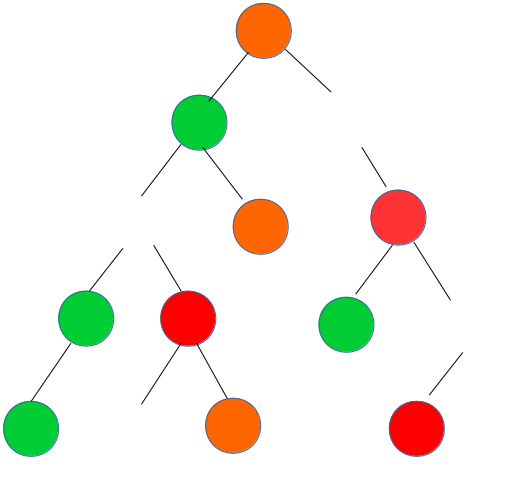
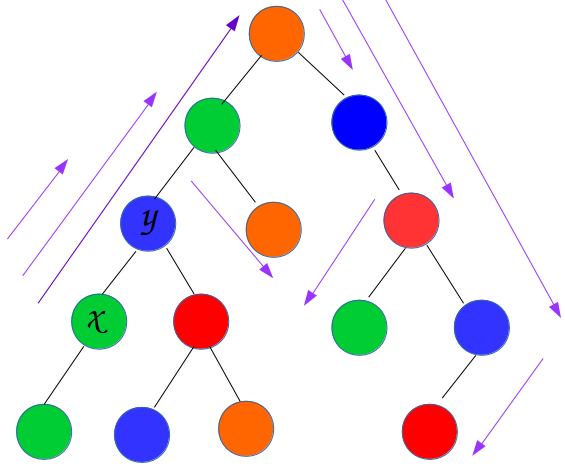
我们不妨看一看图中的点\(x\),
到小树外任意一点的路径上都经过点\(y\),且经过的第一个蓝点就是\(y\)。
看图感性理解一下吧。
所以,每个点在删除一种颜色以后,这种颜色对每个点的贡献为\((n-siz)\)(其中\(siz\)为小树大小)。
每个点所有颜色的贡献为\((n-siz_{1})+(n-siz_{2})+...+(n-siz_{num})=n*num-\sum_{i=1}^{num}siz_{i}\)
注意:每个点自己的颜色的贡献为n,因为在到每个点的路径上,它都是第一个此颜色的点。
将每棵小树的大小存于根处(\(dfs\)),
最后统计(\(get_ans\))。
再说一下咱数组的定义。
\(c[x]:x\)的颜色,\(v[x]:\)表示这种颜色是否出现,\(siz[x]:\)x的字数大小,\(sz:\)删除父亲颜色后的小树大小,
\(sub[x]:\)记录删除颜色为\(x\)的点后,与此小树不连通的点数大小,\(pre[x]:\)删除颜色为x的点后,上一棵小树的大小(父亲祖辈上的)
\(ans[x]:\)答案,\(sum:\) 目前此点被覆盖的小树的大小之和。
总共分为两步:\(dfs()\)和get_ans()$上面讲了)
我就贴贴代码,贴贴图片吧:
\(1.dfs():\)
void dfs(int x,int fa){
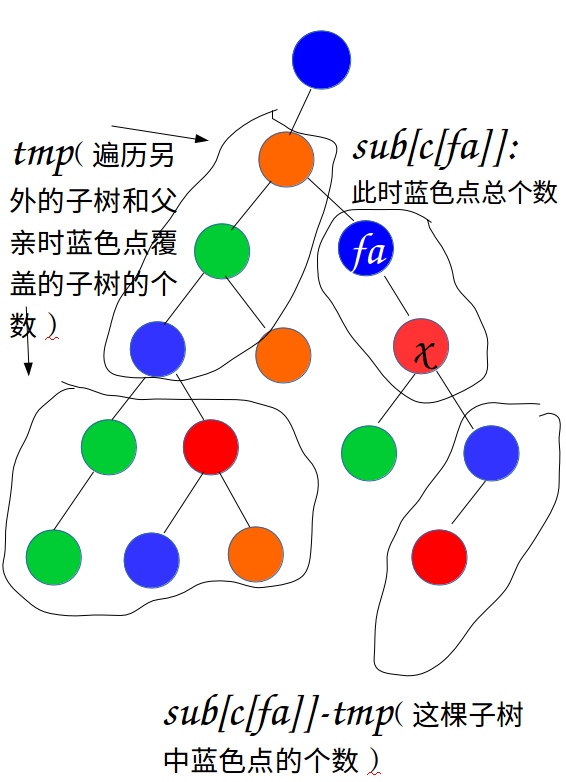
siz[x]=1; ll tmp=sub[c[fa]];//储存这棵子树外的sub(包括其它子树和父辈)
FOR(i,x)
if(e[i].to!=fa)
dfs(e[i].to,x),siz[x]+=siz[e[i].to];//求x的子树大小
++sub[c[x]];//删去此点
if(fa) sz[x]=siz[x]-sub[c[fa]]+tmp,sub[c[fa]]+=sz[x];//sz[x]:求以x为根的小树大小,sub更新,图中有详解
}
2.get_ans():
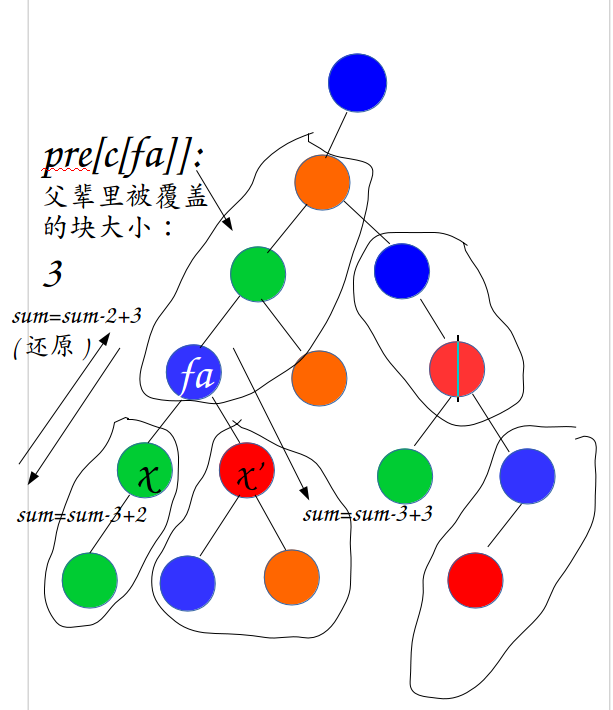
void get_ans(int x,int fa){
ll tmp=pre[c[fa]];//记录父辈里之前一块的被此颜色覆盖的点数
sum+=sz[x]-tmp,pre[c[fa]]=sz[x],ans[x]=n*num-sum+pre[c[x]];
//sum将颜色为c[fa]的块大小更新,pre也更新,ans的式子上面有解释
FOR(i,x)
if(e[i].to!=fa)
get_ans(e[i].to,x);
pre[c[fa]]=tmp,sum-=sz[x]-tmp;
//还原,不将影响带到另一棵子树
}
注意:\(++sub[c[x]]\)不能放在\(if(fa)\)之后,因为存在父亲儿子颜色相同的情况,在此情况中:
还有,处理一下根节点的情况,剩下的就是它的。
总代码:
#include<bits/stdc++.h>
#define ll long long
#define For(i,l,r) for(int i=(l);i<=(r);++i)
#define FOR(i,x) for(int i=head[x];i;i=e[i].nxt)
using namespace std;
const int N=1e5+6;
int t1,t2,cnt=0,c[N],v[N],siz[N],sz[N],sub[N],head[N];
ll n,num=0,sum=0,pre[N],ans[N];
struct edge{int nxt,to;}e[N<<1];
inline void add(int u,int v){e[++cnt].nxt=head[u],e[cnt].to=v,head[u]=cnt;}
inline int rd(){
int T=0,F=1; char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-') F=-1; ch=getchar();}
while(ch>='0'&&ch<='9') T=(T<<3)+(T<<1)+(ch-48),ch=getchar();
return F*T;
}
void dfs(int x,int fa){
siz[x]=1; ll tmp=sub[c[fa]];//储存这棵子树外的sub(包括其它子树和父辈)
FOR(i,x)
if(e[i].to!=fa)
dfs(e[i].to,x),siz[x]+=siz[e[i].to];//求x的子树大小
++sub[c[x]];//删去此点
if(fa) sz[x]=siz[x]-sub[c[fa]]+tmp,sub[c[fa]]+=sz[x];//sz[x]:求以x为根的小树大小,sub更新,图中有详解
}
void get_ans(int x,int fa){
ll tmp=pre[c[fa]];//记录父辈里之前一块的被此颜色覆盖的点数
sum+=sz[x]-tmp,pre[c[fa]]=sz[x],ans[x]=n*num-sum+pre[c[x]];
//sum将颜色为c[fa]的块大小更新,pre也更新,ans的式子上面有解释
FOR(i,x)
if(e[i].to!=fa)
get_ans(e[i].to,x);
pre[c[fa]]=tmp,sum-=sz[x]-tmp;
//还原,不将影响带到另一棵子树
}
int main(){
n=read();
For(i,1,n){
c[i]=read();
if(!v[c[i]]) v[c[i]]=1,++num;
}
For(i,1,n-1) t1=read(),t2=read(),add(t1,t2),add(t2,t1);
dfs(1,0);
For(i,1,1e5) if(v[i]) sum+=n-sub[i],pre[i]=n-sub[i]; //特殊处理根节点
get_ans(1,0);
For(i,1,n) printf("%lld\n",ans[i]);
return 0;
}
温馨提示:代码临时拼凑,并一定能对哦,但理解起来没问题。


