最小树形图(朱刘算法)学习笔记

最小树形图(朱刘算法)学习笔记

蒟蒻理解不透彻的地方还请各位dalao多多包涵。

树形图，应该就是指能从根节点到达其他节点的有向的树形结构，

最小树形图则是权值和最小的树形图(废话)

一般来说,分为三步：

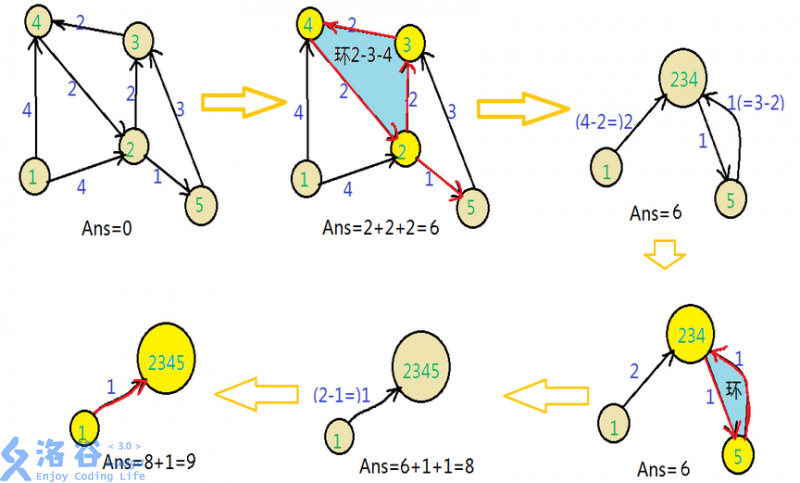
1.选出每个点的最短边[同一个环中的不算]，并记录(为判环缩环作准备)。（若有点无最短边，则树形图无解）

2.判断最短边是否能构成环。（不能构成环则结束）

3.缩环为点。

注:所选出的边可能不是一棵树

cnt=0;
for(int i=1;i<=n;++i) ine[i]=inf,vis[i]=0,id[i]=0;//预处理
for(int i=1;i<=m;++i) if(q[i].x!=q[i].y&&ine[q[i].y]>q[i].c) ine[q[i].y]=q[i].c,pre[q[i].y]=q[i].x;//每个点的最短边
for(int i=1;i<=n;++i) if(i!=rt&&ine[i]==inf) return -1;//有点无最短边

for(int i=1;i<=n;++i){
    if(i==rt) continue;
    ans+=ine[i],t=i;//加贡献
    while(vis[t]!=i&&!id[t]&&t!=rt) vis[t]=i,t=pre[t];
    //能走到环的点或者换上的点停下
    if(!id[t]&&t!=rt){
          id[t]=++cnt; //将环上的点标记为新的环
          for(int o=pre[t];o!=t;o=pre[o]) id[o]=cnt;
    }
}//找环
if(!cnt) break;//无环结束

for(int i=1;i<=n;++i) if(!id[i]) id[i]=++cnt;
for(int i=1;i<=m;++i){
    t=q[i].y,q[i].x=id[q[i].x],q[i].y=id[q[i].y];
    if(q[i].x!=q[i].y) q[i].c-=ine[t];
}
n=cnt,rt=id[rt];
//去旧图,换新图

代码：

#include<bits/stdc++.h>
using namespace std;
const int N=106,M=10006,inf=2e8;
int n,m,rt,t,cnt=0,id[N],pre[N],ine[N],vis[N];
struct line{int x,y,c;}q[M];
inline int read(){
   int T=0,F=1; char ch=getchar();
   while(ch<'0'||ch>'9'){if(ch=='-') F=-1; ch=getchar();}
   while(ch>='0'&&ch<='9') T=(T<<3)+(T<<1)+(ch-48),ch=getchar();
   return F*T;
}
int zl(){
    int ans=0;
    while(true){
         cnt=0;
         for(int i=1;i<=n;++i) ine[i]=inf,vis[i]=0,id[i]=0;//预处理
         for(int i=1;i<=m;++i) if(q[i].x!=q[i].y&&ine[q[i].y]>q[i].c) ine[q[i].y]=q[i].c,pre[q[i].y]=q[i].x;//每个点的最短边
         for(int i=1;i<=n;++i) if(i!=rt&&ine[i]==inf) return -1;//有点无最短边
         for(int i=1;i<=n;++i){
             if(i==rt) continue;
             ans+=ine[i],t=i;
             while(vis[t]!=i&&!id[t]&&t!=rt) vis[t]=i,t=pre[t];
             //能走到环的点或者换上的点停下
             if(!id[t]&&t!=rt){
                id[t]=++cnt; //将环上的点标记为新的环
                for(int o=pre[t];o!=t;o=pre[o]) id[o]=cnt;
             }
         }//找环
         if(!cnt) break;//无环结束
         for(int i=1;i<=n;++i) if(!id[i]) id[i]=++cnt;
         for(int i=1;i<=m;++i){
             t=q[i].y,q[i].x=id[q[i].x],q[i].y=id[q[i].y];
             if(q[i].x!=q[i].y) q[i].c-=ine[t];
         }
         n=cnt,rt=id[rt];
         //去旧图,换新图
    }
    return ans;
}
int main(){
    n=read(),m=read(),rt=read();
    for(int i=1;i<=m;++i) q[i].x=read(),q[i].y=read(),q[i].c=read();
    printf("%d\n",zl());
    return 0;
} 

拓展，无根树的最小树形图：

建一个超级源点，以他为根。