教科书般的亵渎题解

教科书般的亵渎题解

先吐槽一波，这名字起的，没玩过游戏的人怕是都以为是什么题啊 

原题链接

洛谷P4593 [TJOI2018]教科书般的亵渎
题目描述
小豆喜欢玩游戏，现在他在玩一个游戏遇到这样的场面,每个怪的血量为a_i，且每个怪物血量均不相同，小豆手里有无限张“亵渎”。亵渎的效果是对所有的怪造成1点伤害，如果有怪死亡，则再次施放该法术。我们认为血量为0怪物死亡

小豆使用一张 “亵渎”会获得一定的分数，分数计算如下，在使用一张“亵渎”之后，每一个被亵渎造成伤害的怪会产生x^k,其中造成伤害前怪的血量为x和需要杀死所有怪物所需的“亵渎”的张数k。

输入格式
第一行输入一个T(T≤10)，表示有多少组测试数据

每组组测试数据第一行为n，m，表示有当前怪物最高的血量n，和m种没有出现的血量

接下来m行，每行11个数a，表示场上没有血量为a_i的怪物

输出格式
一共T行，每行一个数，第i行表示第i组测试数据中小豆的最后可以获得的分数, 因为这个分数会很大需要模10^9+7

输入输出样例
输入 #1 复制
2
10 1
5
4 2
1
2
输出 #1 复制
415
135
说明/提示
对于%10的数据，有m=0

对于%20的数据，有m≤1

对%30%的数据，有m≤2

对于%40%的数据，有m≤3

对于%50%的数据，有m≤4

对于%60%的数据，有m≤5

对于%100%的数据，有m≤50

对于%100%的数据，有n≤10¹³

题意：

开始看了半天想了5、6个小时不知道怎么做，结果发现理解错了题意，一定不是我的错，一定是题目的锅

有一种群体技能，每次能造成群体伤害一点，并且若有怪死亡会自动重放(不计入分数)。

每一次放技能会有x^k分数，其中x为怪血量总和，k为杀死所有怪的最少放技能次数。

有两点要注意：1.技能会重放。2.k为初始值，是不变量，并不是当前量，作者惨死当场

对，你没看错，因为作者太弱，不知怎么概括，所以······，几乎就抄的题目

思路：

每个存在的怪都会有血量x^k的分数贡献。

又仔细看题，发现m的范围极小。

所以想到容斥，答案即为：

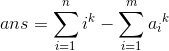 （k=m+1）

显然可以用拉格朗日插值法代入0到k+1解决，

你问为什么它是个k+1次多项式？

我也不是很清楚，或许可以参考这里。

则直接暴力枚举即可。

#include<bits/stdc++.h>
using namespace std;
const int N=56;
const long long mod=1e9+7;
int tt,m;
long long n,g,ans,a[N],t[N],x[N],y[N];
inline long long read(){
    long long T=0,F=1; char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-') F=-1; ch=getchar();}
    while(ch>='0'&&ch<='9') T=(T<<3)+(T<<1)+(ch-48),ch=getchar();
    return F*T;
}
long long ksm(long long u,long long v){
     long long base=u,answer=1;
     while(v){
          if(v&1) answer=answer*base%mod;
          base=base*base%mod,v>>=1;
     }
     return (answer+mod)%mod;
}
long long mul(long long k){
    g=1;
    long long o,answer=0;
    if(k<=m+3) return y[k];
    for(int i=1;i<=m+3;++i) g=g*(k-i+mod)%mod;
    for(int i=1;i<=m+3;++i){
        o=ksm(k-i,mod-2)*g%mod*y[i]%mod*t[i]%mod;
        answer=(answer+o+mod)%mod;
    }
    return answer;
}
long long init(int x){
   long long answer=0;
   for(int i=x+1;i<=m;++i) answer=(answer+ksm(a[i]-a[x],m+1)+mod)%mod;
   return answer;
}
int main(){
   tt=read();
   while(tt--){
        memset(t,0,sizeof(t)); memset(x,0,sizeof(x)); memset(y,0,sizeof(y)); memset(a,0,sizeof(a));
        n=read(),m=read(),a[0]=0,ans=0;
        for(int i=1;i<=m;++i) a[i]=read();
        sort(a+1,a+m+1);
        for(int i=1;i<=m+3;++i) x[i]=i,y[i]=(y[i-1]+ksm(i,m+1))%mod;
        for(int i=1;i<=m+3;++i){
            t[i]=1;
            for(int j=1;j<=m+3;++j) if(i!=j) t[i]=t[i]*(i-j+mod)%mod;
            t[i]=ksm(t[i],mod-2);
        }
        for(int i=0;i<=m;++i) ans=(ans+mul(n-a[i])+mod-init(i))%mod;
        printf("%lld\n",ans);
   }
   return 0;
}